Презентация на тему: Курс лекций по теоретической механике. Динамика

Курс лекций по теоретической механике Динамика (I часть)Электронный учебный курс написан на основе лекций, читавшихся автором для студентов, обучавшихся по специальностям СЖД, ПГС и СДМ в НИИЖТе и МИИТе (1974-2006 гг.). Учебный материал соответствует календарным планам в объеме трех семестров.Для полной реализации анимационных эффектов при презентации необходимо использовать средство просмотра Power Point не ниже, чем встроенный в Microsoft Office операционной системы Windows-ХР Professional.Замечания и предложения можно послать по e-mail: [email protected] .

Содержание Лекция 1. Введение в динамику. Законы и аксиомы динамики материальной точки. Основное уравнение динамики. Дифференциальные и естественные уравнения движения. Две основные задачи динамики. Примеры решения прямой задачи динамикиЛекция 2. Решение обратной задачи динамики. Общие указания к решению обратной задачи динамики. Примеры решения обратной задачи динамики. Движение тела, брошенного под углом к горизонту, без учета сопротивления воздуха. Лекция 3. Прямолинейные колебания материальной точки. Условие возникновения колебаний. Классификация колебаний. Свободные колебания без учета сил сопротивления. Затухающие колебания. Декремент колебаний.Лекция 4. Вынужденные колебания материальной точки. Резонанс. Влияние сопротивления движению при вынужденных колебаниях.Лекция 5. Относительное движение материальной точки. Силы инерции. Частные случаи движения для различных видов переносного движения. Влияние вращения Земли на равновесие и движение тел.Лекция 6. Динамика механической системы. Механическая система. Внешние и внутренние силы. Центр масс системы. Теорема о движении центра масс. Законы сохранения. Пример решения задачи на использование теоремы о движении центра масс.Лекция 7. Импульс силы. Количество движения. Теорема об изменении количества движения. Законы сохранения. Теорема Эйлера. Пример решения задачи на использование теоремы об изменении количества движения. Момент количества движения. Теорема об изменении момента количества движения.. Лекция 8. Законы сохранения. Элементы теории моментов инерции. Кинетический момент твердого тела. Дифференциальное уравнение вращения твердого тела. Пример решения задачи на использование теоремы об изменении момента количества движения системы. Элементарная теория гироскопа.Рекомендуемая литература1. Яблонский А.А. Курс теоретической механики. Ч.2. М.: Высшая школа. 1977 г. 368 с.2. Мещерский И.В. Сборник задач по теоретической механике. М.: Наука. 1986 г. 416 с.3. Сборник заданий для курсовых работ /Под ред. А.А. Яблонского. М.:Высшая школа. 1985 г. 366 с.4. Бондаренко А.Н. “Теоретическая механика в примерах и задачах. Динамика” (электронное пособие www.miit.ru/institut/ipss/faculties/trm/main.htm ), 2004 г.

Динамика – раздел теоретической механики,изучающий механическое движение с самой общей точкизрения. Движение рассматривается в связи с действующимина объект силами. Раздел состоит из трех отделов: ■ Динамика точки – изучает движение материальной точки с учетом сил, вызывающих это движение. Основной объект - материальная точка – материальное тело, обладающей массой, размерами которого можно пренебречь. ■ Динамика механической системы – изучает движение совокупности материальных точек и твердых тел, объединяемых общими законами взаимодействия, с учетом сил, вызывающих это движение. ■ Аналитическая механика – изучает движение несвободных механических систем с использованием общих аналитических методов.Основные допущения:– существует абсолютное пространство (обладает чисто геометрическими свойствами, не зависящими от материи и ее движения .– существует абсолютное время (не зависит от материи и ее движения).Отсюда вытекает:– существует абсолютно неподвижная система отсчета.– время не зависит от движения системы отсчета.– массы движущихся точек не зависят от движения системы отсчета.Эти допущения используются в классической механике, созданной Галилеем и Ньютоном. Она имеет до сих пор достаточно широкую областьприменения, поскольку рассматриваемые в прикладных науках механические системы не обладают такими большими массами и скоростямидвижения, для которых необходим учет их влияния на геометрию пространства, время, движение, как это делается в релятивистской механике(теории относительности). ■ Основные законы динамики – впервые открытые Галилеем и сформулированные Ньютоном составляют основу всех методов описания и анализа движения механических систем и их динамического взаимодействия под действием различных сил.■ Закон инерции (закон Галилея-Ньютона) – Изолированная материальная точка тело сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, приложенные силы не заставят ее изменить это состояние. Отсюда следует эквивалентность состояния покоя и движения по инерции (закон относительности Галилея). Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной. Свойство материальной точки стремиться сохранить неизменной скорость своего движения (свое кинематическое состояние) называется инертностью. ■ Закон пропорциональности силы и ускорения (Основное уравнение динамики - II закон Ньютона) – Ускорение, сообщаемое материальной точке силой, прямо пропорционально силе и обратно пропорционально массе этой точки: или Здесь m – масса точки (мера инертности), измеряется в кг,численно равна весу, деленному на ускорение свободного падения:F – действующая сила, измеряется в Н (1 Н сообщает точке массой 1 кг ускорение 1 м/c2, 1 Н = 1/9.81 кг-с).

■ Закон равенства действия и противодействия (III закон Ньютона) – Всякому действию соответствует равное по величине и противоположно направленное противодействие:Закон справедлив для любого кинематического состояния тел. Силы взаимодействия, будучи приложенные к разным точкам (телам)не уравновешиваются.■ Закон независимости действия сил – Ускорение материальной точки под действием нескольких сил равно геометрической сумме ускорений точки от действия каждой из сил в отдельности: или■ Основное уравнение динамики : Дифференциальные уравнения движения материальной точки:В координатном виде: Используем связь радиуса-вектора с координатами и вектора силы с проекциями: После группировкивекторное соотношениераспадаетсяна три скалярныхуравнения:Естественные уравнения движения материальной точки – получаются проецированием векторного дифференциального уравнения движения на естественные (подвижные) оси координат: или:

Две основные задачи динамики:1. Прямая задача: Задано движение (уравнения движения, траектория). Требуется определить силы, под действием которых происходит заданное движение.2. Обратная задача: Заданы силы, под действием которых происходит движение. Требуется найти параметры движения (уравнения движения, траекторию движения).Обе задачи решаются с помощью основного уравнения динамики и проекции его на координатные оси. Если рассматривается движение несвободной точки, то как и в статике, используется принцип освобождаемости от связей. В результате реакции связей включаются в состав сил, действующих на материальную точку. Решение первой задачи связано с операциями дифференцирования. Решение обратной задачи требует интегрирования соответствующих дифференциальных уравнений и это значительно сложнее, чем дифференцирование. Обратная задача сложнее прямой задачи. Решение прямой задачи динамики - рассмотрим на примерах:Пример 1. Кабина весом G лифта поднимается тросом с ускорением a . Определить натяжение троса. При равномерном движении кабины ay = 0 и натяжение троса равно весу: T = G.При обрыве троса T = 0 и ускорение кабины равно ускорению свободного падения: ay = -g.Таким образом, величина силы пропорциональна расстоянию точки до центра координат инаправлена к центру по линии, соединяющей точку с центром.Траектория движения точки представляет собой эллипс с центром в начале координат:

Лекция 1 (продолжение 1.4) Пример 3: Груз весом G подвешен на тросе длиной l и движется по круговой траектории в горизонтальной плоскости с некоторой скоростью. Угол отклонения троса от вертикали равен . Определить натяжение троса и скорость груза.Подставляем значение реакциитроса, нормального ускоренияво второе уравнение и определяем скорость груза:Пример 4: Автомашина весом G движется по выпуклому мосту (радиус кривизны равен R) со скоростью V. Определить давление автомашины на мост.

Лекция 2 Решение обратной задачи динамики – В общем случае движения точки силы, действующие на точку, являются переменными, зависящими от времени, координат и скорости. Движение точки описывается системой трех дифференциальных уравнений второго порядка: Таким образом, под действием одной и той же системы силматериальная точка может совершать целый класс движений,определяемых начальными условиями.Начальные координаты учитывают исходное положение точки. Начальная скорость, задаваемая проекциями, учитывает влияние на ее движение по рассматриваемому участку траектории сил, действовавших на точку до прихода на этот участок, т.е. начальное кинематическое состояние.Пример 1 решения обратной задачи: Свободная материальная точка массы m движется по действием силы F, постоянной по модулю и величине. . В начальный момент скорость точки составляла v0 и совпадала по направлению с силой. Определить уравнение движение точки.

Лекция 2 (продолжение 2.2) Общие указания к решению прямой и обратной задачи. Порядок решения:1. Составление дифференциального уравнения движения: 1.1. Выбрать систему координат – прямоугольную (неподвижную) при неизвестной траектории движения, естественную (подвижную) при известной траектории, например, окружность или прямая линия. В последнем случае можно использовать одну прямолинейную координату. Начало отсчета совместить с начальным положением точки (при t = 0) или с равновесным положением точки, если оно существует, например, при колебаниях точки.1.2. Изобразить точку в положении, соответствующем произвольному моменту времени (при t > 0) так, чтобы координаты были положительными (s > 0, x > 0). При этом считаем также, что проекция скорости в этом положении также положительна. В случае колебаний проекция скорости меняет знак, например, при возвращении к положению равновесия. Здесь следует принять, что в рассматриваемый момент времени точка удаляется от положения равновесия. Выполнение этой рекомендации важно в дальнейшем при работе с силами сопротивления, зависящими от скорости.

Лекция 2 (продолжение 2.3) Пример 2 решения обратной задачи: Сила зависит от времени. Груз весом P начинает двигаться по гладкой горизонтальной поверхности под действием силы F, величина которой пропорциональна времени (F = kt). Определить пройденное расстояние грузом за время t.1. Выбираем систему отсчета (декартовые координаты) так, чтобы тело имело положительную координату:2. Принимаем объект движения за материальную точку (тело движется поступательно), освобождаем от связи(опорной плоскости) и заменяем реакцией (нормальной реакцией гладкой поверхности):

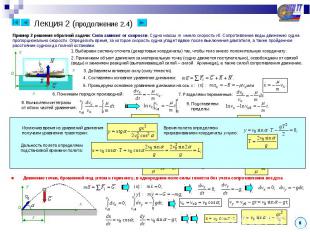
Лекция 2 (продолжение 2.4) Пример 2 решения обратной задачи: Сила зависит от скорости. Судно массы m имело скорость v0. Сопротивление воды движению судна пропорционально скорости. Определить время, за которое скорость судна упадет вдвое после выключения двигателя, а также пройденное расстояние судном до полной остановки.1. Выбираем систему отсчета (декартовые координаты) так, чтобы тело имело положительную координату:2. Принимаем объект движения за материальную точку (судно движется поступательно), освобождаем от связей(воды) и заменяем реакцией (выталкивающей силой – силой Архимеда), а также силой сопротивления движению.3. Добавляем активную силу (силу тяжести).

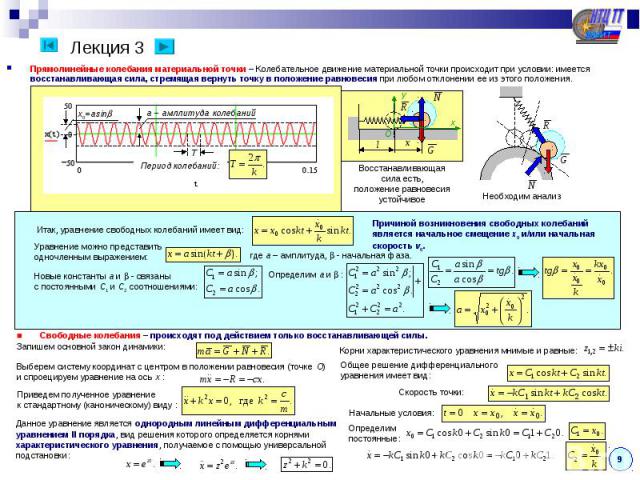
Лекция 3 Прямолинейные колебания материальной точки – Колебательное движение материальной точки происходит при условии: имеется восстанавливающая сила, стремящая вернуть точку в положение равновесия при любом отклонении ее из этого положения. ■ Свободные колебания – происходят под действием только восстанавливающей силы. Запишем основной закон динамики:

Лекция 3 (продолжение 3.2) Затухающие колебания материальной точки – Колебательное движение материальной точки происходитпри наличии восстанавливающей силы и силы сопротивления движению.Зависимость силы сопротивления движению от смещения или скорости определяется физической природысреды или связи, препятствующей движению. Наиболее простой зависимостью является линейная зависимостьот скорости (вязкое сопротивление):

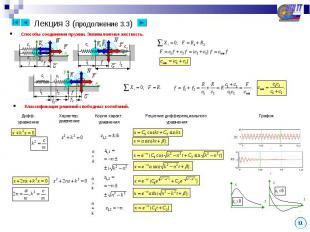
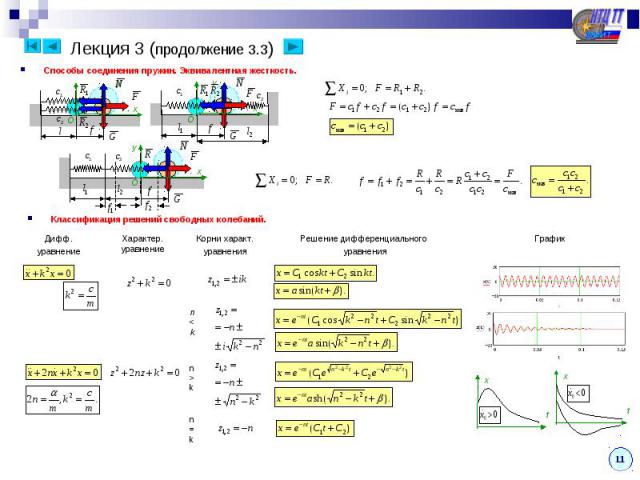
Лекция 3 (продолжение 3.3) Способы соединения пружин. Эквивалентная жесткость.Классификация решений свободных колебаний.

Лекция 4Вынужденные колебания материальной точки – Наряду с восстанавливающей силой действует периодически изменяющаяся сила, называемая возмущающей силой.Возмущающая сила может иметь различную природу. Например, в частном случае инерционное воздействие неуравновешенной массы m1 вращающегося ротора вызывает гармонически изменяющиеся проекции силы: Таким образом, при одновременном действии восстанавливающей и возмущающей сил материальная точка совершает сложное колебательное движение, представляющее собой результат сложения (наложения) свободных (x1) и вынужденных (x2) колебаний.Если p < k (вынужденные колебания малой частоты),то фаза колебаний совпадает с фазой возмущающей силы:

Лекция 4 (продолжение 4.2) Коэффициент динамичности – отношение амплитуды вынужденных колебанийк статическому отклонению точки под действием постоянной силы H = const:Резонанс – возникает, когда частота вынужденных колебаний совпадает с частотой собственных колебаний (p = k). Это наиболее часто происходит при запуске и остановке вращения плохо сбалансированных роторов, закрепленных на упругих подвесках. Дифференциальное уравнение колебаний при равенстве частот:

Лекция 5 Относительное движение материальной точки – Положим, что подвижная (неинерциальная) система координат Oxyz движется по некоторому закону относительно неподвижной (инерциальной) системы координат O1x1y1z1. Движение материальной точки M (x, y, z) относительно подвижной системы Oxyz– относительное, относительно неподвижной системы O1x1y1z1– абсолютное. Движение подвижной системы Oxyz относительно неподвижной системы O1x1y1z1– переносное движение.

Лекция 5 (продолжение 5.2) Влияние вращения Земли на движение тел в поле тяготения Земли – Положим тело падает на Землю с некоторой высоты H над поверхностью Земли на широте φ . Выберем подвижную систему отсчета, жестко связанную с Землей, направляя оси x, y по касательной к параллели и к меридиану:Таким образом, влияние вращения Земли на движение телчрезвычайно мало для практических высот и скоростей ив технических расчетах не учитывается. Из решения второго уравнения также следует существованиескорости по оси y, которая также должна вызывать и вызываетсоответствующее ускорение и силу инерции Кориолиса.Влияние этой скорости и силы инерции, связанной с ней,на изменение движения будет еще меньше, чемрассмотренная сила инерции Кориолиса, связанная свертикальной скоростью.

Лекция 6 Динамика механической системы.Система материальных точек или механическая система – Совокупность материальных точек или материальных тех, объединяемых общими законами взаимодействия (положение или движение каждой из точек или тела зависит от положения и движения всех остальных)Система свободных точек - движение которых не ограничивается никакими связями (например, планетная система, в которой планеты рассматриваются как материальные точки).Система несвободных точек или несвободная механическая система – движение материальных точек или тел ограничиваются наложенными на систему связями (например, механизм, машина и т.п.).Силы, действующие на систему. В дополнение к ранее существовавшей классификации сил (активные и реактивные силы) вводится новаяклассификация сил:1. Внешние силы (e) – действующие на точки и тела системы со стороны точек или тел, не входящих в состав данной системы.2. Внутренние силы (i) – силы взаимодействия между материальными точками или телами, входящими в данную систему.Одна и та же сила может являться как внешней, так и внутренней силой. Все зависит от того, какая механическая система рассматривается.Например: В системе Солнце, Земля и Луна все силы тяготения между ними являются внутренними. При рассмотрении системы Земля и Луна силытяготения, приложенные со стороны Солнца – внешние: На основании закона действия и противодействия каждой внутренней силе Fk соответствует другая внутренняясила Fk’, равная по модулю и противоположная по направлению.Из этого следуют два замечательных свойства внутренних сил:Главный вектор всех внутренних сил системы равен нулю:Главный момент всех внутренних сил системы относительнолюбого центра равен нулю: Или в проекциях на координатные оси:Замечание. Хотя эти уравнения похожи на уравнения равновесия, они таковыми не являются, поскольку внутренние силы приложены к различным точкам или телам системы и могут вызывать движение этих точек (тел) относительно друг друга. Из этих уравнений следует,что внутренние силы не влияют на движение системы, рассматриваемой как одно целое.Центр масс системы материальных точек. Для описания движения системы в целом вводится геометрическая точка, называемой центром масс, радиус-вектор которой определяетсявыражением, где M – масса всей системы:

Лекция 6 (продолжение 6.2) Теорема о движении центра масс системы – Рассмотрим систему n материальных точек. Приложенные к каждой точке силы разделим на внешние и внутренние и заменим их на соответствующие равнодействующие Fke и Fki. Запишем для каждой точки основное уравнение динамики: илиСледствия из теоремы о движении центра масс системы(законы сохранения):1. Если в интервале времени [t1, t2] главный вектор внешних сил системыравен нулю, Re = 0, то скорость центра масс постоянна, vC = const(центр масс движется равномерно прямолинейно – закон сохранениядвижения центра масс).2. Если в интервале времени [t1, t2] проекция главного вектора внешних силсистемы на ось x равна нулю, Rxe = 0, то скорость центра масс по оси xпостоянна, vCx = const (центр масс движется по оси равномерно).Аналогичные утверждения справедливы для осей y и z.Пример: Два человека массами m1 и m2 находятся в лодке массой m3.В начальный момент времени лодка с людьми находилась в покое.Определить перемещение лодки, если человек массой m2 пересел к носу лодки на расстояние а.

Лекция 7 Импульс силы – мера механического взаимодействия, характеризующая передачу механического движения со стороны действующих на точку сил за данный промежуток времени:Теорема об изменении количества движения системы – Рассмотрим систему n материальных точек. Приложенные к каждой точке силы разделим на внешние и внутренние и заменим их на соответствующие равнодействующие Fke и Fki. Запишем для каждой точки основное уравнение динамики: или

Лекция 7 (продолжение 7.2) Следствия из теоремы об изменении количества движения системы(законы сохранения):1. Если в интервале времени [t1, t2] главный вектор внешних сил системыравен нулю, Re = 0, то вектор количества движения постоянен, Q = const– закон сохранения количества движения системы).2. Если в интервале времени [t1, t2] проекция главного вектора внешних силсистемы на ось x равна нулю, Rxe = 0, то проекция количества движениясистемы на ось x постоянна, Qx = const. Аналогичные утверждения справедливы для осей y и z.Пример: Граната массы M, летевшая со скоростью v, разорвалась на две части. Скорость одного из осколков массы m1 возросла в направлении движения до величины v1. Определить скорость второго осколка.

Лекция 7 (продолжение 7.3) Момент количества движения точки или кинетический момент движения относительно некоторого центра – мера механического движения, определяемая вектором, равным векторному произведению радиуса-вектора материальной точки на вектор ее количества движения:Кинетический момент системыматериальных точек относительнонекоторого центра – геометрическаясумма моментов количеств движенийвсех материальных точек относительноэтого же центра:Теорема об изменении момента количества движения системы – Рассмотрим систему n материальных точек. Приложенные к каждой точке силы разделим на внешние и внутренние и заменим их на соответствующие равнодействующие Fke и Fki. Запишем для каждой точки основное уравнение динамики: или

Лекция 8 ■ Следствия из теоремы об изменении момента количества движения системы (законы сохранения):1. Если в интервале времени [t1, t2] вектор главного момента внешних сил системы относительно некоторого центра равен нулю, MOe = 0, то вектор момента количества движения системы относительно этого же центра постоянен, KO = const – закон сохранения момента количества движения системы).2. Если в интервале времени [t1, t2] главный момент внешних сил системы относительно оси x равен нулю, Mxe = 0, то момент количества движения системы относительно оси x постоянен, Kx = const. Аналогичные утверждения справедливы для осей y и z.■ Элементы теории моментов инерции – При вращательном движении твердого тела мерой инерции (сопротивления изменению движения) является момент инерции относительно оси вращения. Рассмотрим основные понятия определения и способы вычисления моментов инерции. 1. Момент инерции материальной точки относительно оси:

Лекция 8 (продолжение 8.2) Момент инерции однородного стержня постоянногосечения относительно оси:5. Момент инерции однородного сплошного цилиндра относительно оси симметрии:Для вычисления момента инерции относительно центральнойоси (проходящей через центр тяжести) достаточно изменитьрасположение оси и задать пределы интегрирования (-L/2, L/2).Здесь продемонстрируем формулу перехода к параллельнымосям:Здесь использована формула объема цилиндра V=πR2H.Для вычисления момента инерции пустотелого (толстого) цилиндрадостаточно задать пределы интегрирования от R1 до R2 (R2> R1):В силу малости толщины цилиндрасчитаем, что все точки находятсяна одинаковом расстоянии R до осии интегрирования не требуется.Объем V = 2πRtH. (тонкий цилиндррадиуса R с толщиной стенки t). Поскольку высота цилиндров в результате не входит в формулы моментов инерции, то они остаются справедливыми для тонкого сплошного диска и обода колеса (тонкого кольца).Кинетический момент вращающегося тела равен произведению угловой скорости на момент инерции относительно оси вращения.

Лекция 8 (продолжение 8.3) Пример: Два человека одинакового веса G1 = G2 висят на канате, переброшенном через сплошной блок весом G3 = G1/4. В некоторый момент один из них начал подниматься по канату с относительной скоростью u. Определить скорости подъема каждого из людей.После начала движения одного человека относительно каната вся система пришла в движение, но кинетический момент системы должен остаться равным нулю: Kz = 0.Кинетический момент системы складывается из кинетических моментов обоих людей и блока:Пример: Определить период малых свободных колебаний однородного стержня массы M и длиной l, подвешенного одним концом к неподвижной оси вращения.

Лекция 8 (продолжение 8.4 – дополнительный материал) ■ Элементарная теория гироскопа:Гироскоп – твердое тело, вращающееся вокруг оси материальной симметрии, одна из точек которой неподвижна.Свободный гироскоп – закреплен так, что его центр масс остается неподвижным, а ось вращения проходит через центр масс и может принимать любое положение в пространстве, т.е. ось вращения изменяет свое положение подобно оси собственного вращения тела при сферическом движении.Основное допущение приближенной (элементарной) теории гироскопа – вектор момента количествадвижения (кинетический момент) ротора считается направленным вдоль собственной оси вращения.Таким образом, несмотря на то, что в общем случае ротор участвует в трех вращениях, принимается в расчеттолько угловая скорость собственного вращения ω = dφ/dt. Основанием для этого является то, чтов современной технике ротор гироскопа вращается с угловой скоростью порядка 5000-8000 рад/c(около 50000-80000 об/мин), в то время как две другие угловые скорости, связанные с прецессией и нутациейсобственной оси вращения в десятки тысяч раз меньше этой скорости. Основное свойство свободного гироскопа – ось ротора сохраняет неизменное направление в пространстве по отношению к инерциальной (звездной) системе отсчета (демонстрируется маятником Фуко, сохраняющим неизменной по отношению к звездам плоскость качания, 1852 г.).Это вытекает из закона сохранения кинетического момента относительно центра масс ротора при условии пренебрежения трением в подшипниках осей подвески ротора, внешней и внутренней рамы:Действие силы на ось свободного гироскопа. В случае действия силы, приложенной к оси ротора,момент внешних сил относительно центра масс не равен нулю:Производная кинетического момента по времениравна скорости конца этого вектора (теорема Резаля):Это означает, что ось ротора будет отклоняться не в сторону действия силы, а в сторону вектора моментаэтой силы, т.е. будет поворачиваться не относительно оси x (внутренняя подвеска), а относительно оси y(внешняя подвеска).При прекращении действия силы ось ротора останется в неизменном положении, соответствующемпоследнему моменту времени действия силы, т.к. с этого момента времени момент внешних сил вновь становитсяравным нулю. В случае кратковременного действия силы (удара) ось гироскопа практически не меняет своегоположения.Таким образом, быстрое вращение ротора сообщает гироскопу способность противодействовать случайным воздействиям,стремящимся изменить положение оси вращения ротора, а при постоянном действии силы сохраняет положение плоскости,перпендикулярной действующей силе, в которой лежит ось ротора. Эти свойства используются в работе инерциальных систем навигации.