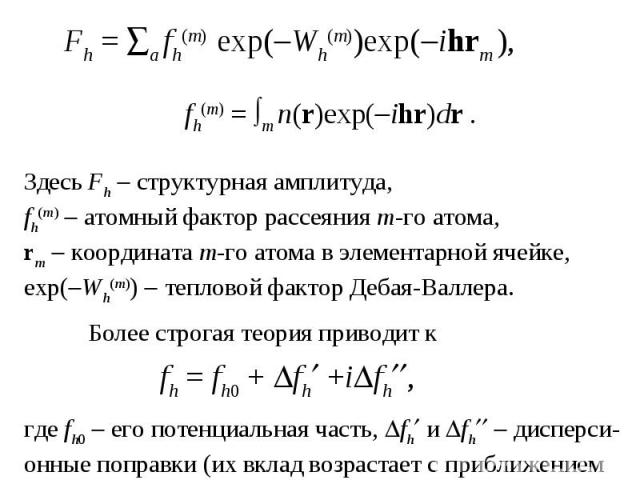Презентация на тему: Динамическая теория дифракции рентгеновских лучей в кристаллах

Динамическая теория дифракции рентгеновских лучей в кристаллах (лекция)

Дорогие коллеги !!! Это не научный доклад в бешенном ритме. Это ЛЕКЦИЯ !!! Поэтому прошу задавать ЛЮБЫЕ вопросы прямо во время чтения лекции !!!!

Общие сведения о рентгеновском излучении 2. Уравнения Максвелла 3. Кинематическое приближение 4. А так ли нам она нужна, эта самая динами- ческая теория ?? 5. Основные положения и уравнения динамической теории дифракции. Два подхода к этой теории. 6. Граничные условия. Геометрии Брэгга и Лауэ. Коэффициенты отражения и прохождения. 7. Некоторые примеры

Рентгеновские лучи (X-rays) – электромагнитное излучение с длиной волны rат d 1 Ангстрема = 10-8 см = 0.1 нм. Именно поэтому они применяются для .... Энергия рентгеновских фотонов ћ 10 кэВ >> энергии связи не слишком глубоких электронов Открытие X-rays – Вильгельм Конрад Рентген (1895 г.) Нобелевская премия (первая в мире) – 1901 г. ... и это всегда приятно напомнить другому физическому, но не рентгеновскому люду, а именно: оптикам, акустикам, магнетологам, радиофизикам, астрономам, гонцами за новыми элементарными частицами, искателями кварков и других темных и скрытых материй, энергий и действенных идей....)
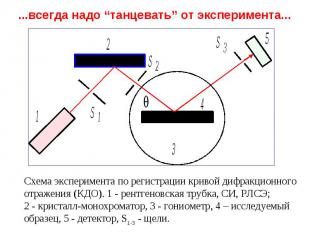
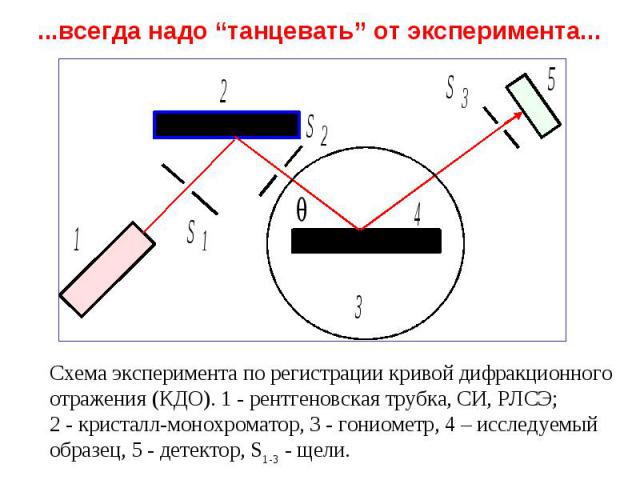
всегда надо “танцевать” от эксперимента

Микроскопические уравнения Максвелла

Макроскопическое уравнение Максвелла

Материальное уравнение (линейный случай

Метод преобразований (интегралов) Фурье

Простейший случай. Излучение в вакууме (P = 0, D = E) Из уравнения Максвелла следует, что k2 = ( /c)2

Мы чуть не упустили такое решение: k = k΄ + ik΄΄ (комплексный вектор, в вакууме, как это не звучит пародоксально !!!!) Условие прежнее: k2 = k΄2 - k΄΄2 + 2ik΄k΄΄ = ω2/c2 Отсюда: k΄2 - k΄΄2 = k2; k΄k΄΄ = 0.

рентгеновском диапазоне вдали от краев поглоще- ния связь между P и E локальная и изотропная (!!)

При больших частотах смещение электрона x определяется вторым законом Ньютона md2x/dt2 = eE. Отсюда смещение x = (e/m 2)E, а поляризация P = exn(r), где n(r) - плотность электронов

Видно, что величина 0 крайне мала и отрицательна. Последнее приводит, в частности, к явлению полного внешнего отражения (ПВО) РЛ (в отличие от полного внутреннего отражения в оптике видимого диапазона, для которого 0 > 0).

Есть два понятия (подхода) в физике рассеяния рентгеновских лучей: 1. Кинематическая теория (а лучше и правильнее сказать – приближение) 2. Динамическая теория (как наиболее точная и адекватная)

Аксиомы кинематической теории

Кинематическое рассеяние
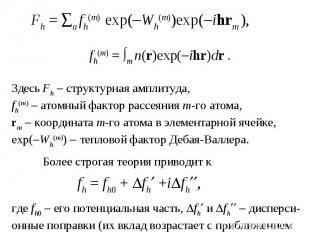
Здесь Fh структурная амплитуда, fh(m) атомный фактор рассеяния m-го атома, rm координата m-го атома в элементарной ячейке, exp( Wh(m)) тепловой фактор Дебая-Валлера. Более строгая теория приводит к fh = fh0 + fh +i fh , где fh0 его потенциальная часть, fh и fh дисперси- онные поправки (их вклад возрастает с приближением энергии квантов к энергиям электронных переходов
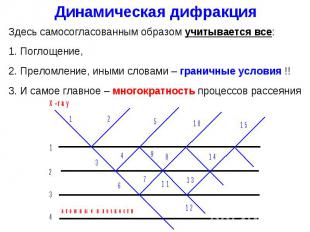
Здесь самосогласованным образом учитывается все: 1. Поглощение, 2. Преломление, иными словами – граничные условия !! 3. И самое главное – многократность процессов рассеяния
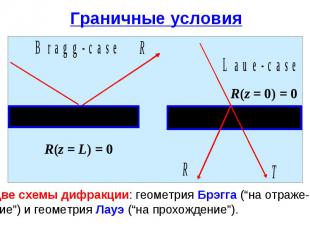
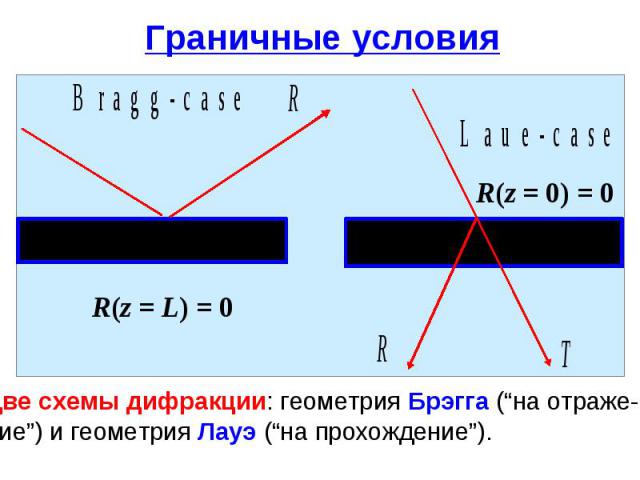
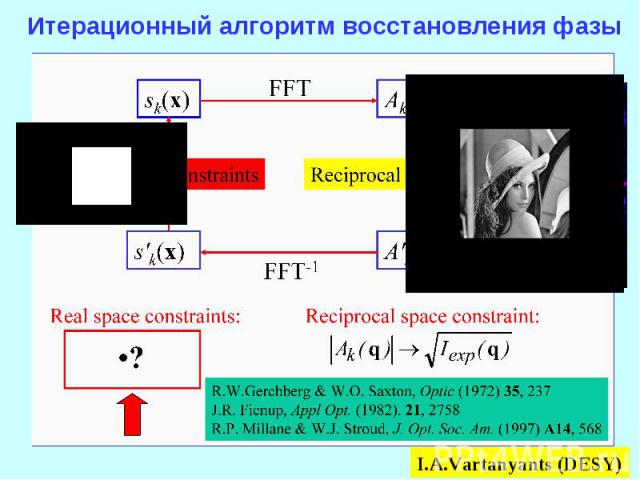
Граничные условия
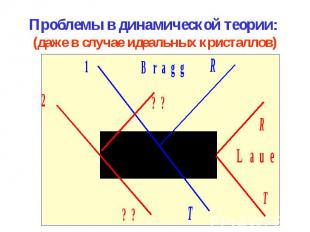
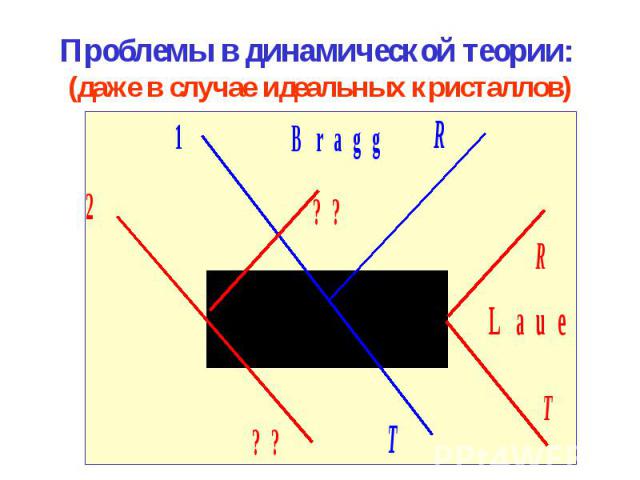
Проблемы в динамической теории: (даже в случае идеальных кристаллов
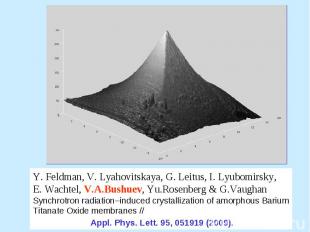
Feldman, V. Lyahovitskaya, G. Leitus, I. Lyubomirsky, E. Wachtel, V.A.Bushuev, Yu.Rosenberg & G.Vaughan Synchrotron radiation–induced crystallization of amorphous Barium Titanate Oxide membranes // Appl. Phys. Lett. 95, 051919 (2009).

В итоге мы приходим к таким состояниям

... А так как объекты малы, то и возникает крамольная мысль – а так ли нам она нужна эта самая динамическая теория ??
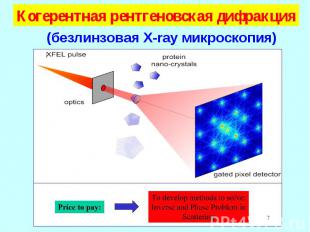
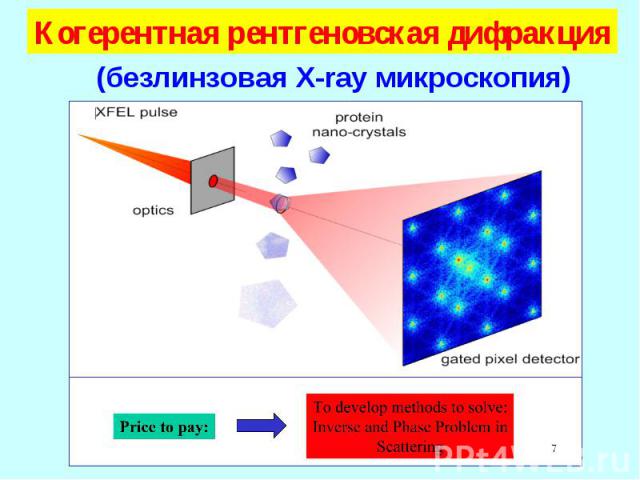
Когерентная рентгеновская дифракция

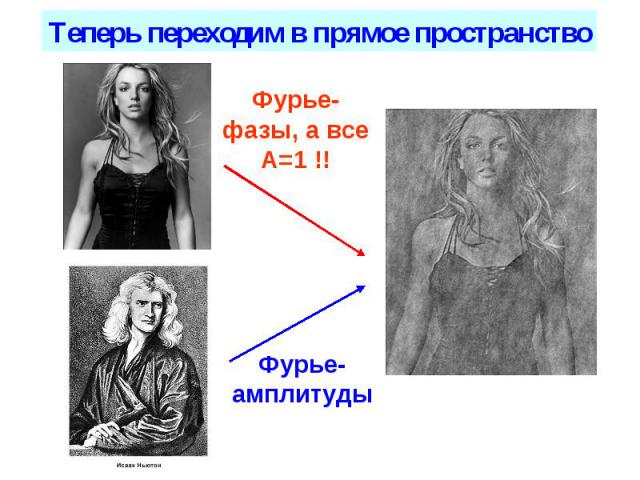
Преобразования Фурье

Преобразования Фурье
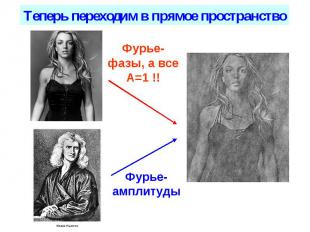
Преобразования Фурье
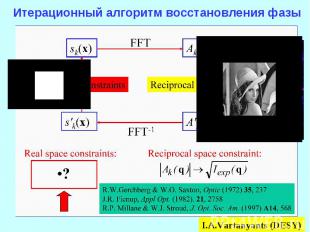
Преобразования Фурье

Преобразования Фурье

Основное уравнение динамической теории

Все это, конечно, хорошо, однако давно пора вернуться к основной теме лекции – к динамической теории дифракции

Основное уравнение динамической теории

Дисперсионное уравнение в двухволновом приближении

Дисперсионное уравнение в двухволновом приближении

Два корня решения дисперсионного уравнения

Два корня решения дисперсионного уравнения

Два корня решения дисперсионного уравнения
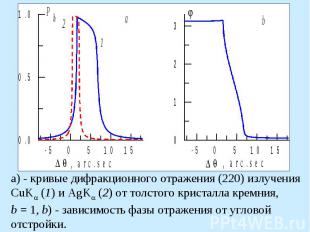
Два корня решения дисперсионного уравнения

Два корня решения дисперсионного уравнения
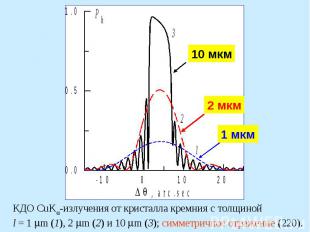
Два корня решения дисперсионного уравнения
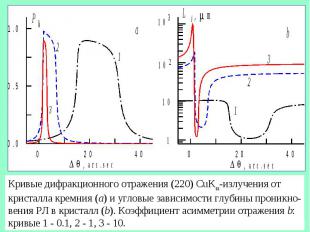
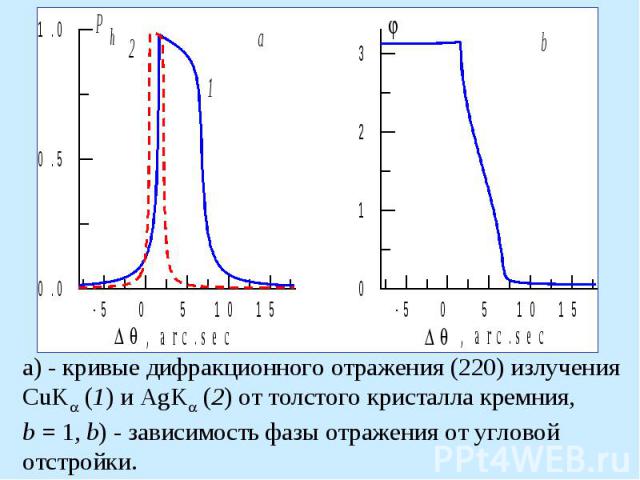
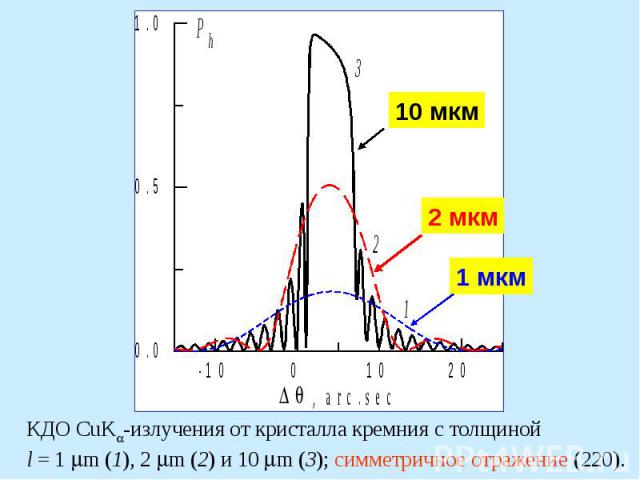
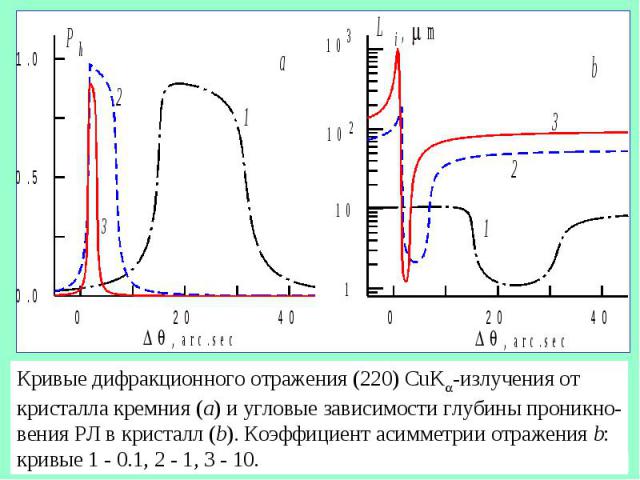
Кривые дифракционного отражения (220) CuK -излучения от кристалла кремния (a) и угловые зависимости глубины проникно- вения РЛ в кристалл (b). Коэффициент асимметрии отражения b: кривые 1 - 0.1, 2 - 1, 3 - 10

Геометрия дифракции Лауэ
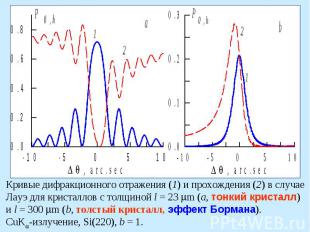
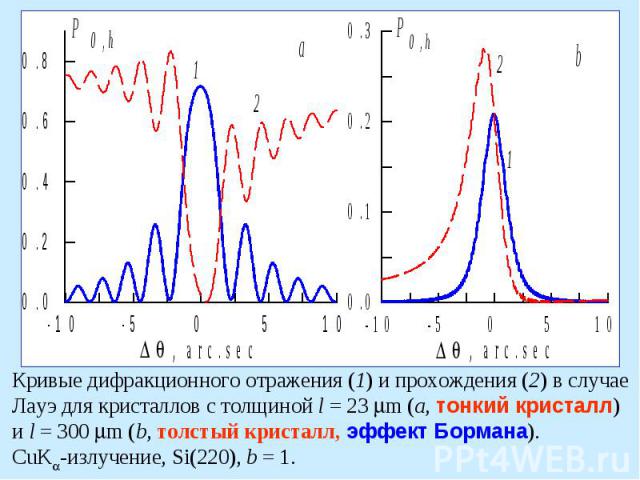
Кривые дифракционного отражения (1) и прохождения (2) в случае Лауэ для кристаллов с толщиной l = 23 m (a, тонкий кристалл) и l = 300 m (b, толстый кристалл, эффект Бормана). CuK -излучение, Si(220), b = 1.

μint(Δθ) = 2k0Im(ε) - интерф. коэффициент поглощения
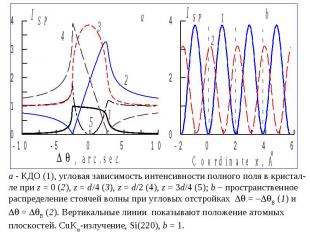
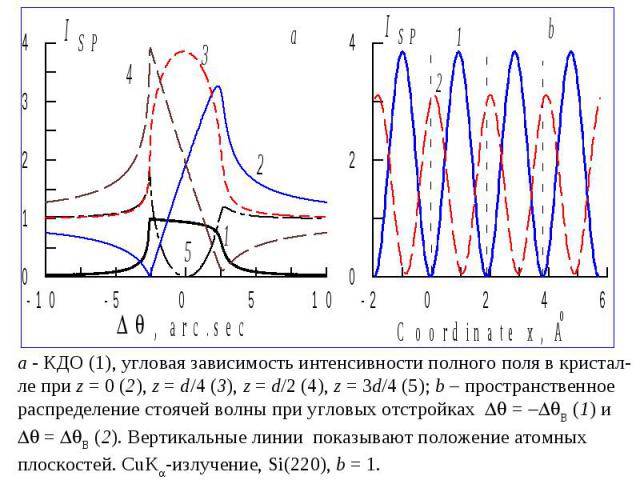
- КДО (1), угловая зависимость интенсивности полного поля в кристал- ле при z = 0 (2), z = d/4 (3), z = d/2 (4), z = 3d/4 (5); b – пространственное распределение стоячей волны при угловых отстройках = B (1) и = B (2). Вертикальные линии показывают положение атомных плоскостей. CuK -излучение, Si(220), b = 1

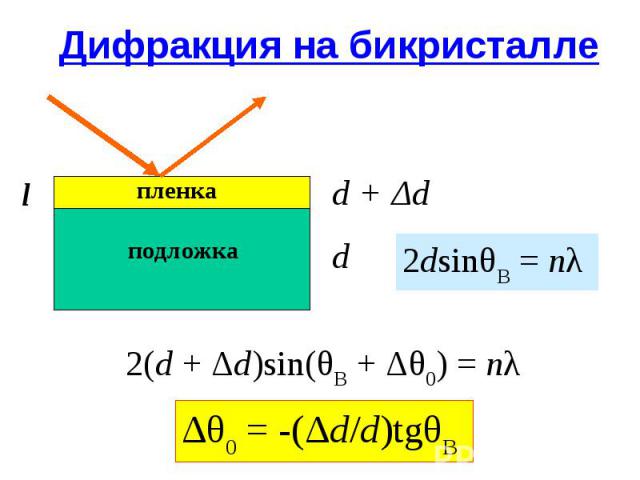
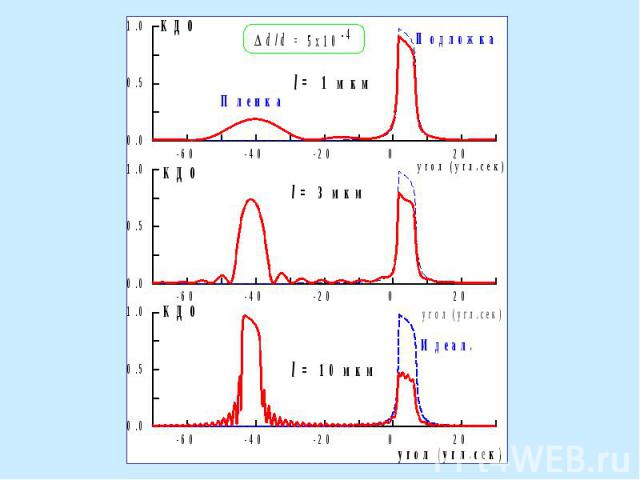
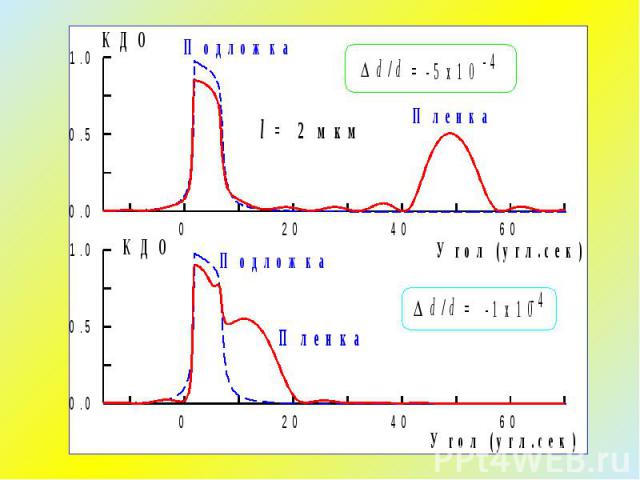
Дифракция на бикристалле
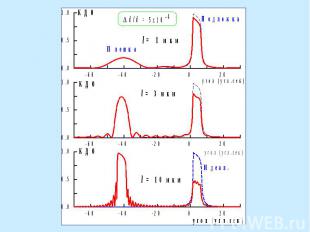
Дифракция на бикристалле
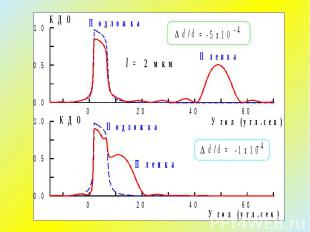
Дифракция на бикристалле
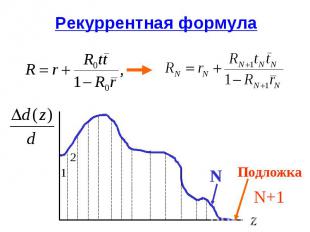
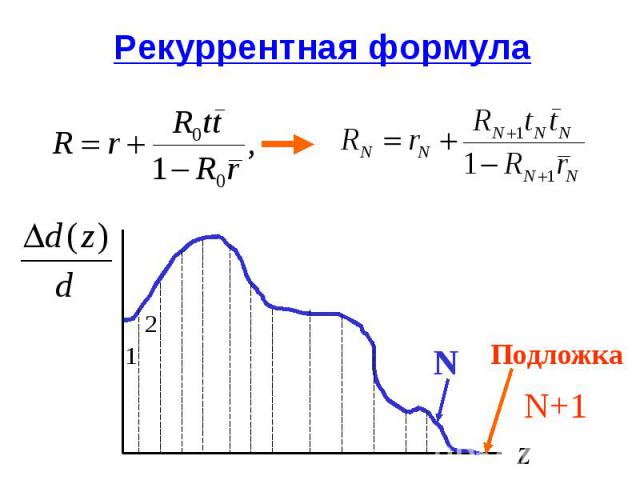
Рекуррентная формула

Уравнения Такаги

Слоистая среда

k0 – волновой вектор в вакууме, kh = k0 + h.

Уравнения Такаги

Уравнение Такаги-Топена
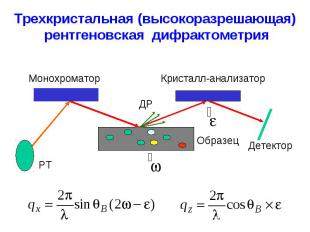
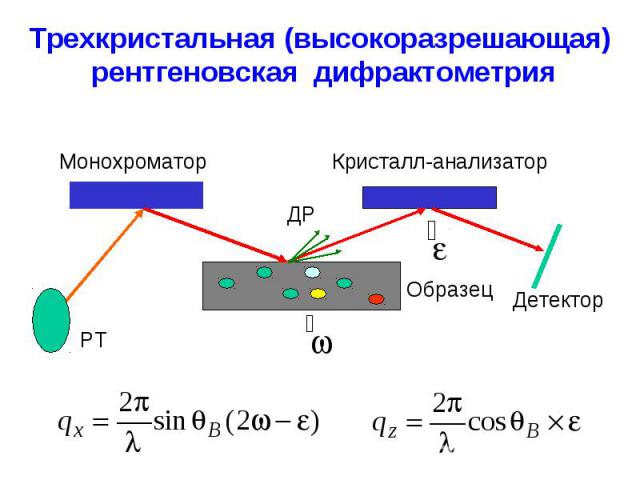
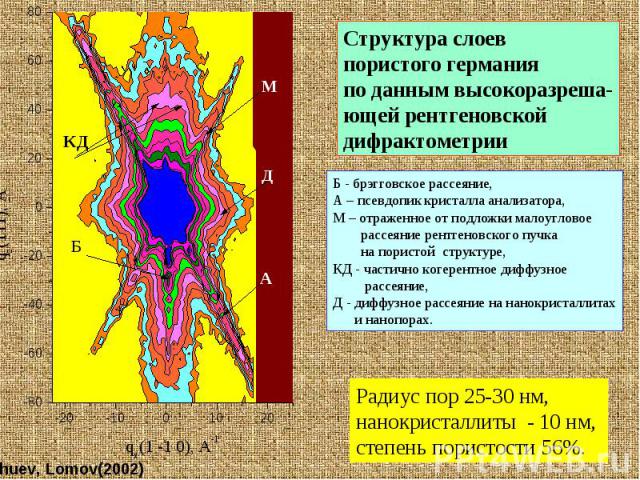
Трехкристальная (высокоразрешающая) рентгеновская дифрактометрия

Трехкристальная (высокоразрешающая) рентгеновская дифрактометрия
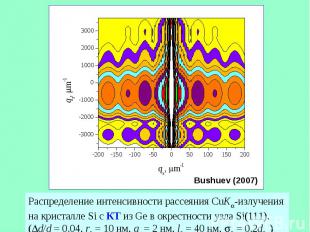
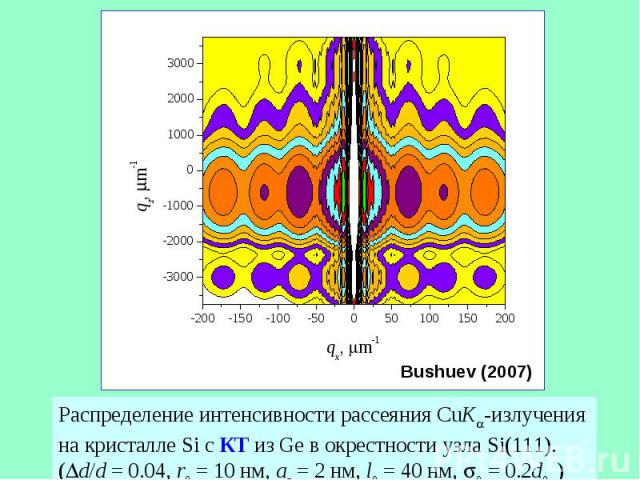
Распределение интенсивности рассеяния CuK -излучения на кристалле Si с КТ из Ge в окрестности узла Si(111). (Dd/d = 0.04, r0 = 10 нм, az = 2 нм, l0 = 40 нм, s0 = 0.2d0 )
Пыль глотать замучаетесь..” (В.В.Путин

Но это еще не все – будет еще одна лекция....