Презентация на тему: Условия принятия управленческих решений

Тема 2. Условия принятия управленческих решений условия определенности, риск и неопределенность при принятии управленческих решений Управленческая экономика

Принятие управленческих решений в условиях определенности Предельный анализ прибыли и затрат Линейное программирование

Предельный доход предприятия Под предельным доходом предприятия понимается среднее изменение выручки предприятия в расчете на единицу продукции в результате изменения величины сбыта на одну единицу.

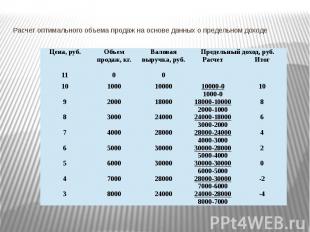
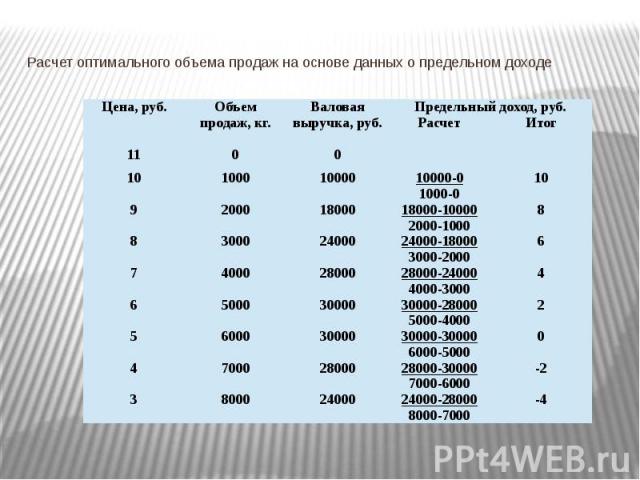
Расчет оптимального объема продаж на основе данных о предельном доходе

Линейное программирование ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ [linear programming] — область математического программирования, посвященная теории и методам решения экстремальных задач, характеризующихся линейной зависимостью между переменными. Предпосылка линейности, когда в реальной экономике подавляющее большинство зависимостей носит более сложный нелинейный характер, представляет собой упрощение действительности.

Линейное программирование

Задача линейного программирования

Решените задачи ЛП Исходя из норм, зафиксированных в таблице, запишем неравенства (ограничения): a11x1 + a12x2 ≤ bi a21x1 + a22x2 ≤ b2 a31x1 + a32x2 ≤ b3. Это означает, что общий расход каждого из трех видов ресурсов не может быть больше его наличия. Поскольку выпуск продукции не может быть отрицательным, добавим еще два ограничения: x1 ≥ 0, x2 ≥ 0. Требуется найти такие значения x1 и x2, при которых общая сумма прибыли, т. е. величина c1 x1 + c2 x2, будет наибольшей или

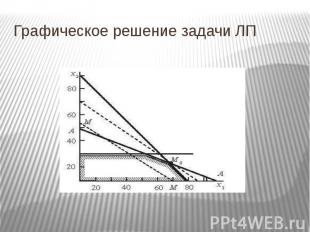
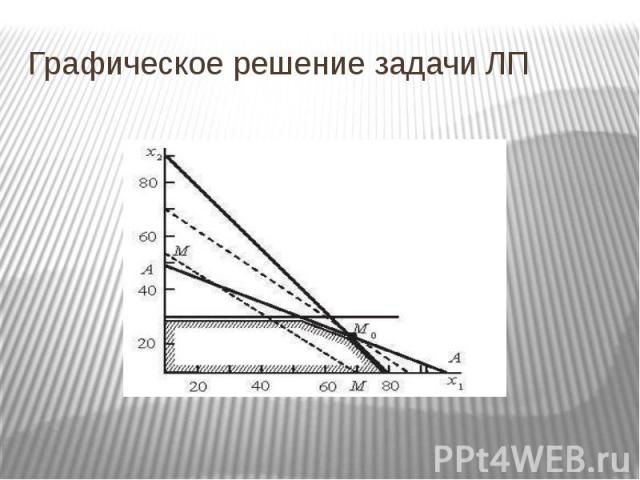
Графическое решение задачи ЛП

Регрессионный анализ Регрессио нный (линейный) анализ — статистический метод исследования зависимости между зависимой переменной Y и одной или несколькими независимыми переменными X1,X2,...,Xp. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными.

Регрессионный анализ Цели регрессионного анализа Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными) Предсказание значения зависимой переменной с помощью независимой(-ых) Определение вклада отдельных независимых переменных в вариацию зависимой

Регрессионный анализ Строго регрессионную зависимость можно определить следующим образом. Пусть Y, X1,X2,...,Xp — случайные величины с заданным совместным распределением вероятностей. Если для каждого набора значений X1 = x1,X2 = x2,...,Xp = xp определено условное математическое ожидание y(x1,x2,...,xp) = E(Y | X1 = x1,X2 = x2,...,Xp = xp) (уравнение линейной регрессии в общем виде), то функция y(x1,x2,...,xp) называется регрессией величины Y по величинам X1,X2,...,Xp, а её график — линией регрессии Y по X1,X2,...,Xp, или уравнением регрессии.