Презентация на тему: Исследование функции с помощью производной

Задачи типа В12 в ЕГЭ Исследование функций. 900igr.net

Правила дифференцирования Производная суммы равна сумме производных. Постоянный множитель можно вынести за знак производной. Производная произведения двух функций равна сумме двух слагаемых; первое слагаемое есть произведение производной первой функции на вторую функцию, а второе слагаемое есть произведение первой функции на производную второй функции. Производная частного

Основные формулы дифференцирования С

Нахождение точки максимума или минимума функции (на отрезке) Нахождение наибольшего и наименьшего значения функции Два типа задач:

Основные определения и теоремы. Теорема 1: Если во всех точках открытого промежутка X выполняется равенство (причем равенство либо не выполняется, либо выполняется лишь в конечном множестве), то функция возрастат на промежутке X Теорема 2: Если во всех точках открытого промежутка X выполняется равенство (причем равенство либо не выполняется, либо выполняется лишь в конечном множестве), то функция возрастат на промежутке X

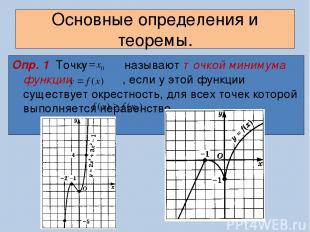
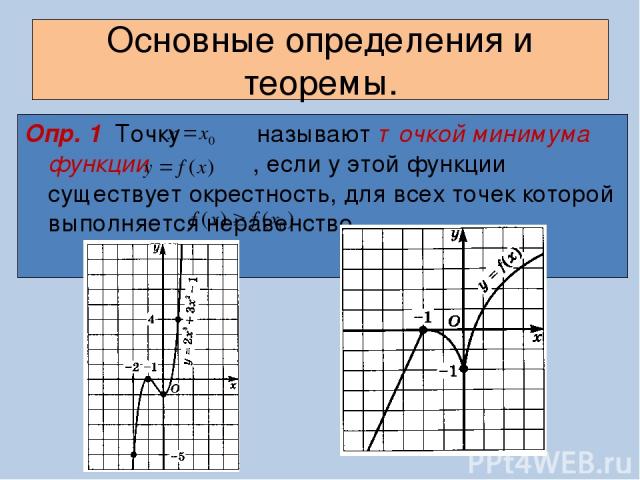
Основные определения и теоремы. Опр. 1 Точку называют точкой минимума функции , если у этой функции существует окрестность, для всех точек которой выполняется неравенство

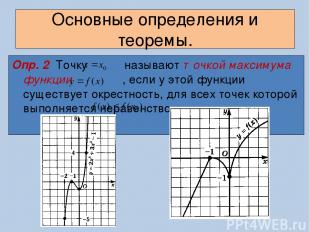
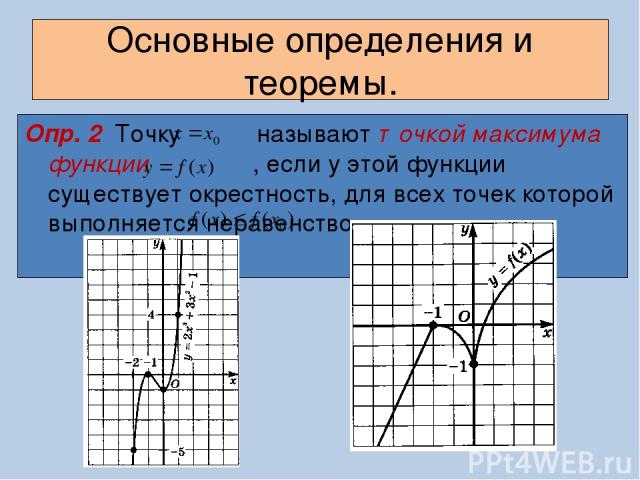
Основные определения и теоремы. Опр. 2 Точку называют точкой максимума функции , если у этой функции существует окрестность, для всех точек которой выполняется неравенство

Основные определения и теоремы. Точки минимума и максимума - точки экстремума. Теорема 3: Если функция имеет экстремум в точке , то в этой точке производная функции либо равна нулю, либо не существует

Основные определения и теоремы. Теорема 4 (Достаточные условие экстремума): Пусть функция непрерывна на промежутке X и имеет внутри промежутка стационарную или критическую точку . Тогда: Если у этой точки существует такая окрестность, в которой при выполняется равенство ,а при – неравенство , то – точка минимума функции Если у этой точки существует такая окрестность, в которой при выполняется равенство , а при – неравенство , то – точка максимума функции Если у этой точки существует такая окрестность, что в ней и слева и справа от точки знаки производной одинаковы, то в точке экстремума нет

Алгоритм нахождения точек экстремума (максимума или минимума) функции. Найти производную Найти стационарные ( )и критические ( не существуют) точки функции Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках. На основании теорем и определений сделать вывод о ее точках экстремума

№1 Найдите точку максимума функции Задачи на нахождение точек экстремума (максимума или минимума) функции. Решение. 1. 2 3. 4.

Решение. 1. 2 3. 4. №1 Найдите точку максимума функции Задачи на нахождение точек экстремума (максимума или минимума) функции.

Задачи для самостоятельного решения на нахождение экстремума функции. Группа А Найдите точку минимума функции Группа В Найдите точку максимума функции Группа С Найдите точку минимума функции Группа D Найдите точку максимума функции

Алгоритм нахождения наименьшего и наибольшего значений непрерывноq функции y= f (x) на отрезке [a;b] Найти производную Найти стационарные и критические точки функции, лежащие внутри отрезка [a;b] Вычислить значения функции в точках, отобранных на втором шаге, и в точках a и b; выбрать среди этих значений наименьшее и наибольшее

Решение. 1. 2 3. №1 Найдите наименьшее значение функции на отрезке [-5;5] Задачи на нахождение наибольшего и наименьшего значения функции.

Задачи для самостоятельного решения на нахождение наибольшего или наименьшего значения Группа А Найдите наибольшее значение функции Группа В Найдите наименьшее значение функции Группа С Найдите наибольшее значение функции Группа D Найдите наименьшее значение функции

Домашняя работа №1954,1977,2041 ЕГЭ 3000 задач с ответами по математике. Все задания группы В. А.Л. Семенов, И.В.Ященко и др. – 3-е издание, - М.:Изд-во «Экзамен», 2012. - 543

Литература Алгебра и начала математического анализа: Учеб. Для 10-11 кл. для учащихся общеобразовательных учреждений (базовый уровень) / Под редакцией А.Г. Мордковича. – М.: Мнемозина, 2009. Алгебра и начала математического анализа: Задачник, Для 10-11 кл. для учащихся общеобразовательных учреждений (базовый уровень) / Под редакцией А.Г. Мордковича. – М.: Мнемозина, 2009. ЕГЭ 2012. Математика. Задача В12. Рабочая тетрадь / Под редакцией А.Л.Семенова и И.В.Ященко – M.: Издательство МЦНМО, 2012