Презентация на тему: Исследование и построение функции

Исследование функций 10 класс Урок обогащающего повторения 5klass.net

Знание законов природы дало человеку возможность объяснять и предсказывать её разнообразнейшие явления. «Математическими портретами» закономерностей природы и служат функции.

Цели и задачи урока: овладевать ключевыми компетенциями самостоятельной исследовательской деятельности; развивать способность систематизировать, сравнивать, обобщать научные знания; на примерах показать широту применения полученных на уроках математических знаний.

Функция - одно из математических и общенаучных понятий Она выражает зависимость между переменными величинами. Любая область знаний – химия, биология, социометрия, лингвистика и многие другие – имеет свои объекты изучения, устанавливает свойства и взаимосвязь между этими объектами.

План урока Проверка домашнего задания. Разгадывание кроссворда. Повторение алгоритма преобразования графика функции. Чётные и нечётные функции. Периодические функции. Построение графика функции с заданными свойствами. Прояви смекалку. Функции в физике. Исследование свойств функции по графику. Домашнее задание. Подведение итогов урока.

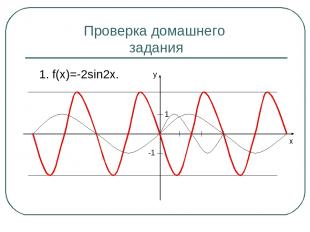
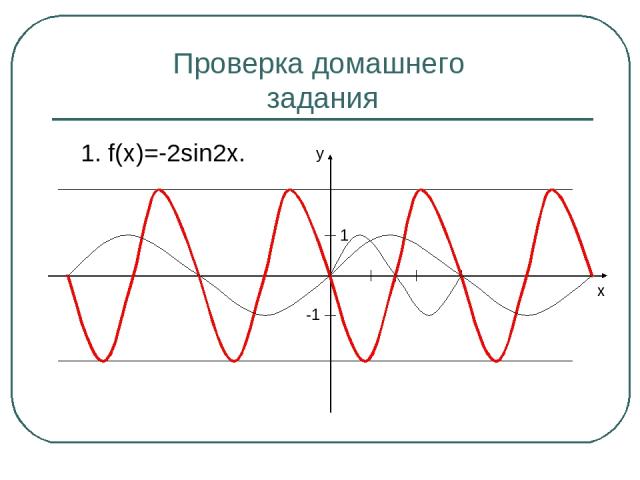
Проверка домашнего задания 1. f(x)=-2sin2x. 1 -1 x y

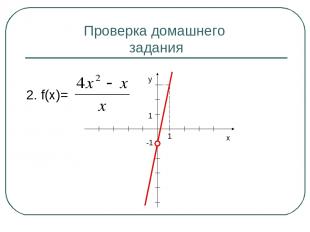
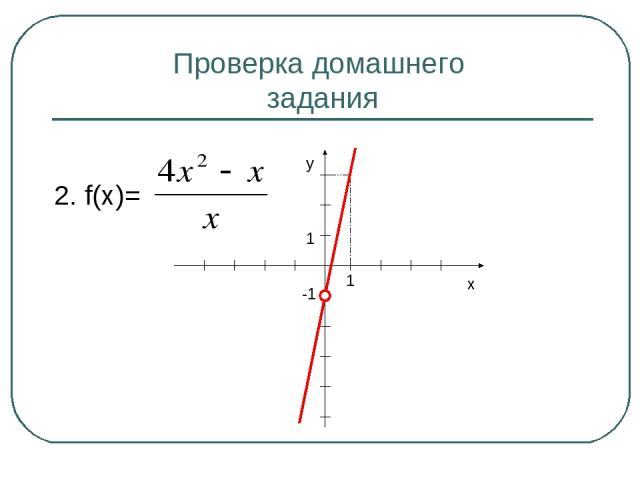
Проверка домашнего задания 2. f(x)= x y 1 1 -1

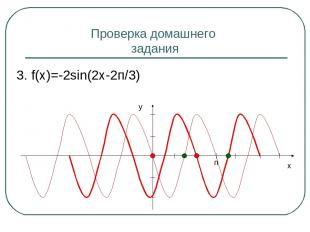
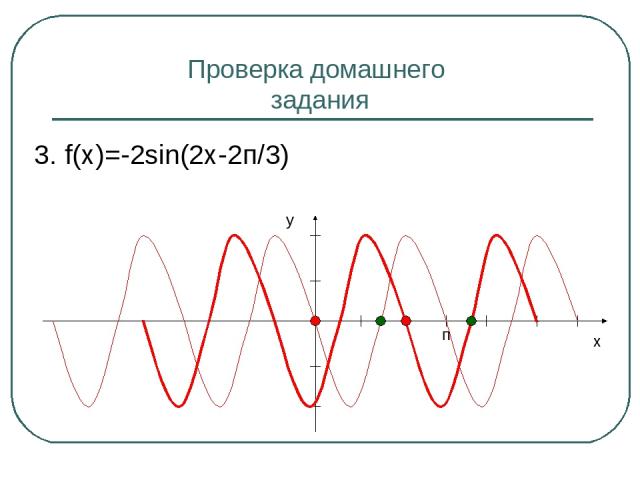
Проверка домашнего задания 3. f(x)=-2sin(2x-2п/3) y x п

Историческая справка Термин «функция» возник в 1664 г. в работах немецкого учёного Лейбница. Ученик Лейбница Бернулли дал в 1718 г. определение функции, свободное от геометрических образов. Его уточнил в своих трудах Эйлер. Символ «f» изобрёл в 1733 г. французский математик Клеро.

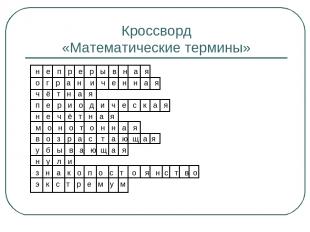
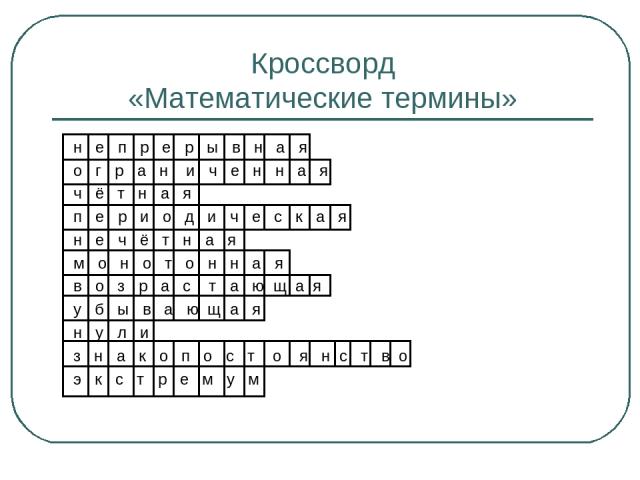
Кроссворд «Математические термины» н е п р е р ы в н а я о г р а н и ч е н н а я ч ё т н а я п е р и о д и ч е с к а я н е ч ё т н а я м о н о т о н н а я в о з р а с т а ю щ а я у б ы в а ю щ а я н у л и з н а к о п о с т о я н с т в о э к с т р е м у м

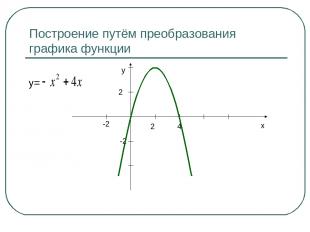
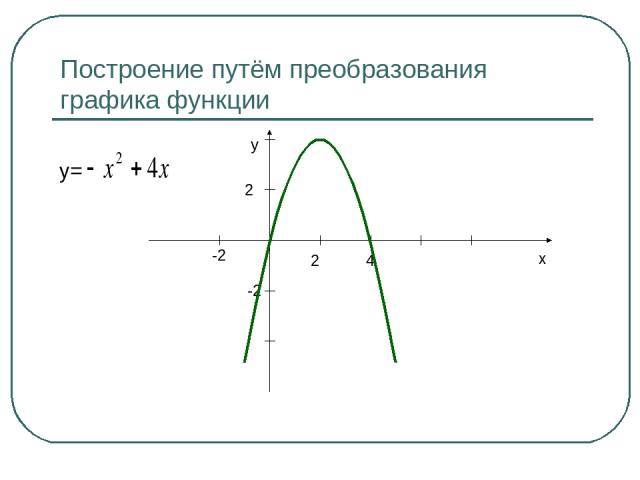
Построение путём преобразования графика функции y= x y 2 4 -2 2 -2

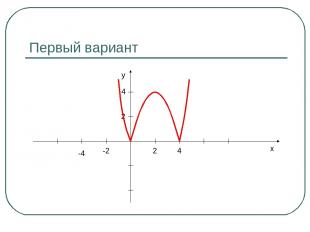
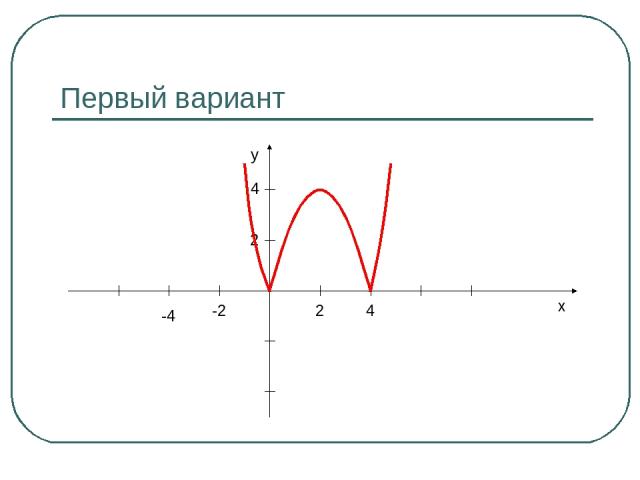
Первый вариант x y 2 4 -2 -4 2 4

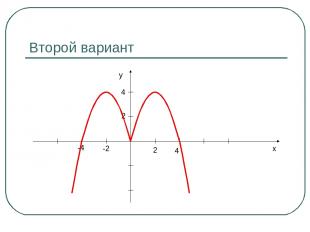
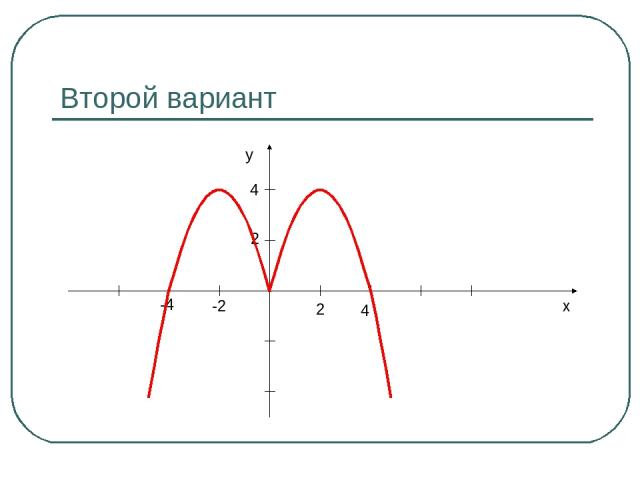
Второй вариант x y 2 4 -2 -4 2 4

Готфрид Вильгельм Лейбниц (1646-1716)

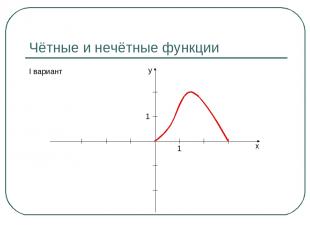
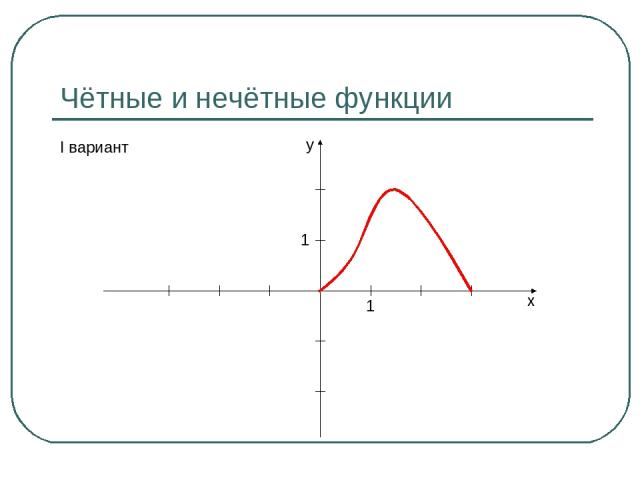
Чётные и нечётные функции I вариант y x 1 1

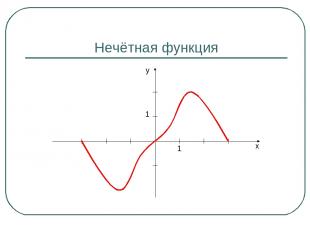
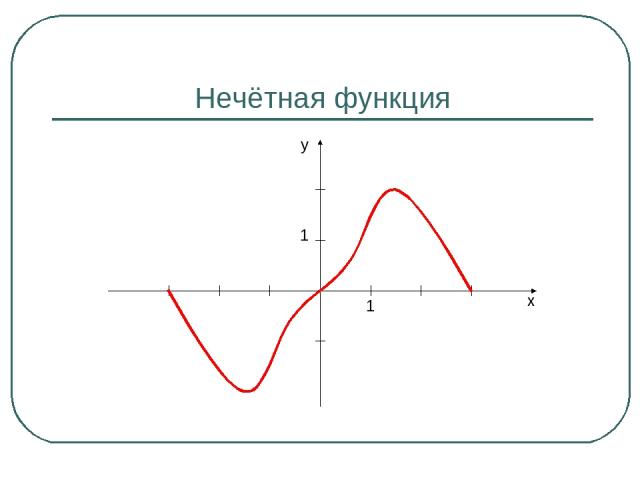
Нечётная функция 1 1 y x

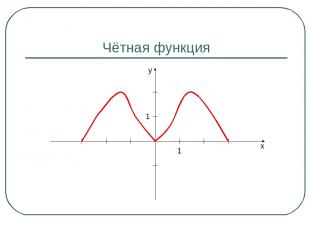
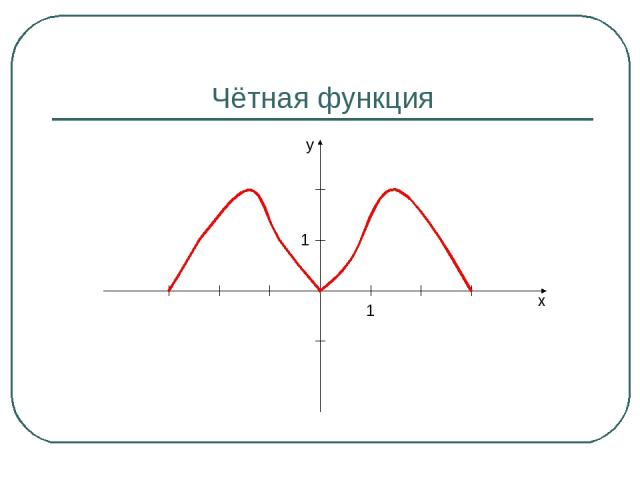
Чётная функция 1 1 y x

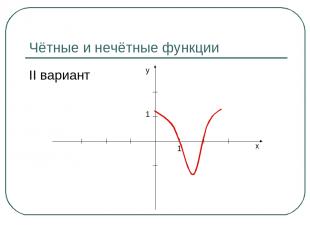
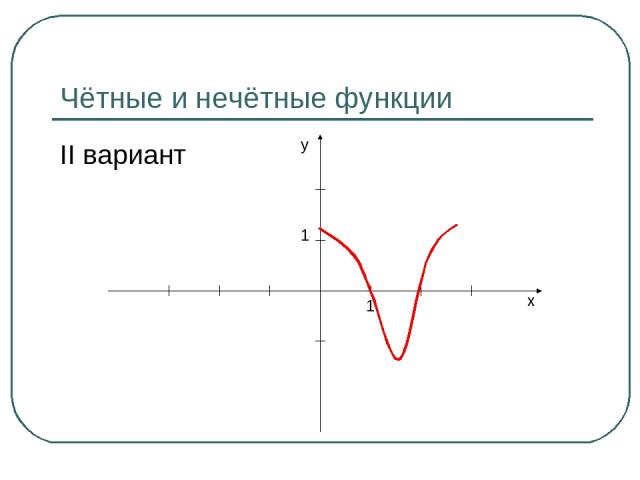
Чётные и нечётные функции II вариант y x 1 1

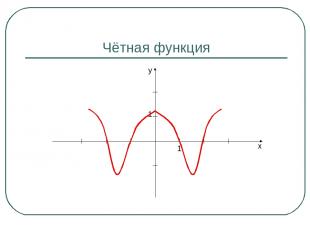
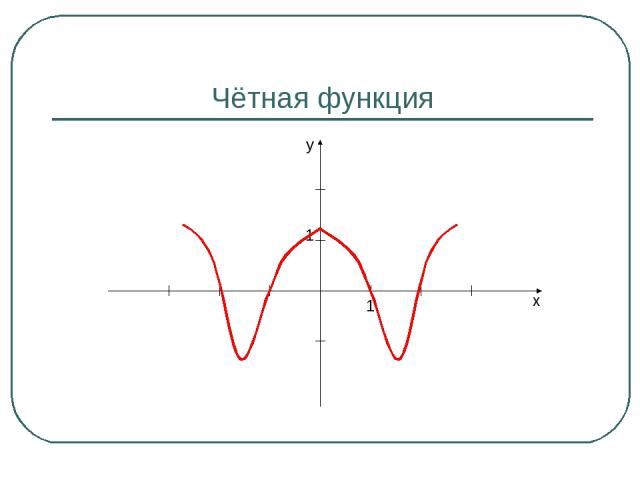
Чётная функция y x 1 1

Иоганн Бернулли (1667-1748)

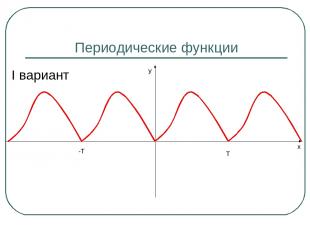
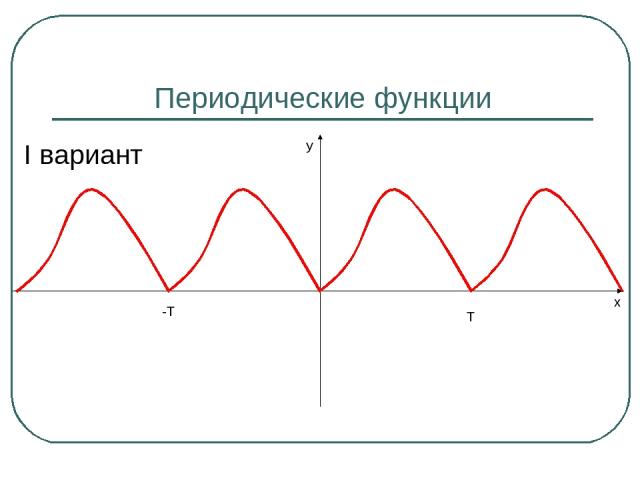
Периодические функции I вариант Т -Т x y

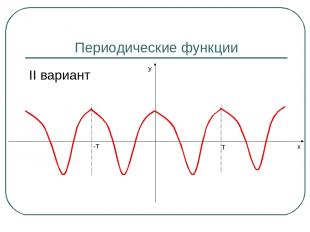
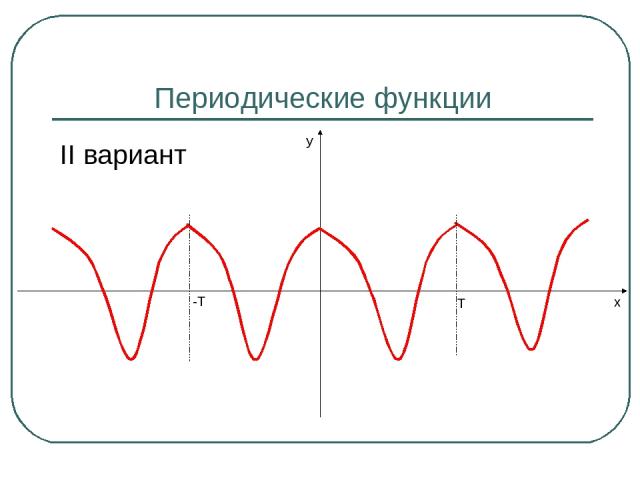
Периодические функции II вариант Т -Т y x

Леонард Эйлер (1707-1783)

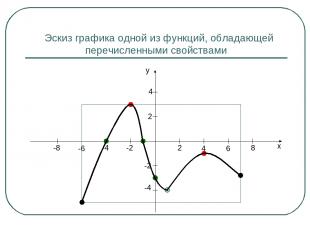
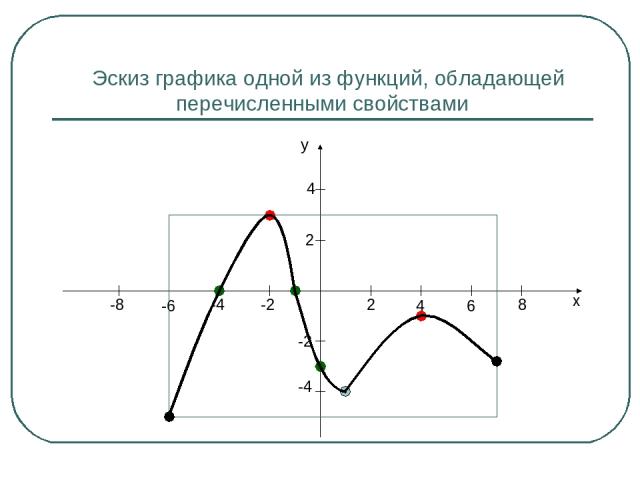
Эскиз графика одной из функций, обладающей перечисленными свойствами x y 2 4 6 8 -2 -4 -6 -8 2 4 -2 -4

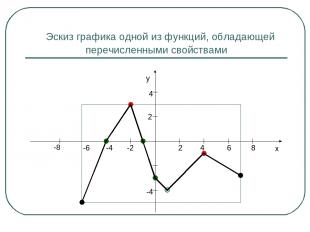
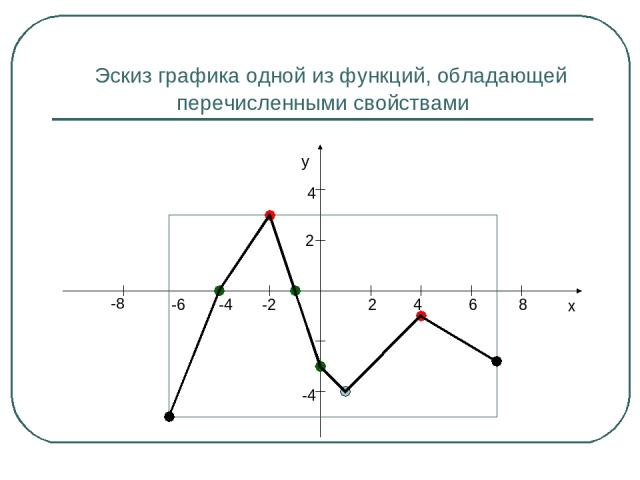
Эскиз графика одной из функций, обладающей перечисленными свойствами y x -2 -4 -6 -8 2 4 2 4 6 8 -4

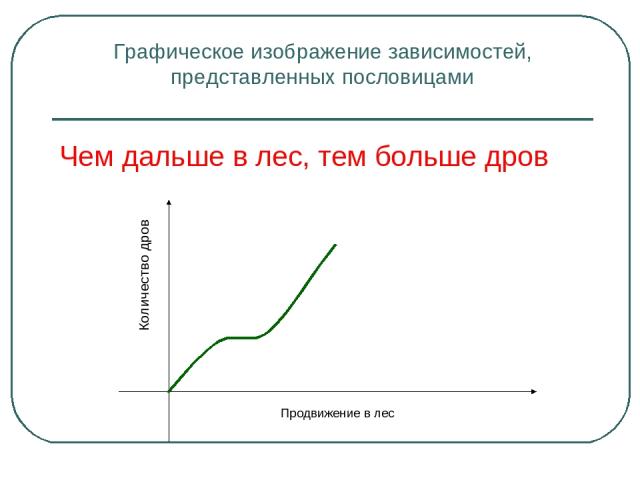
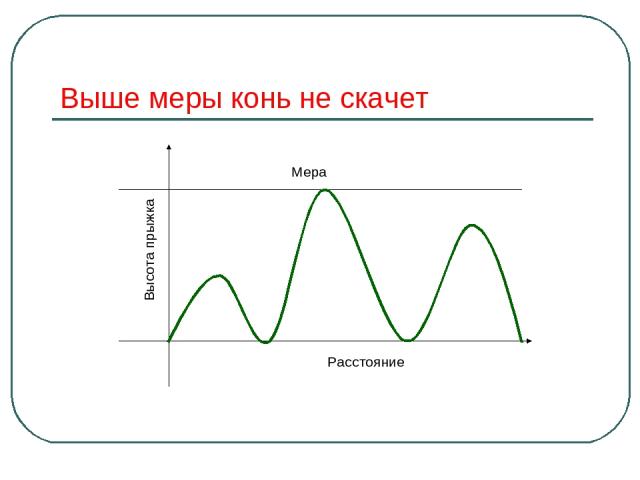
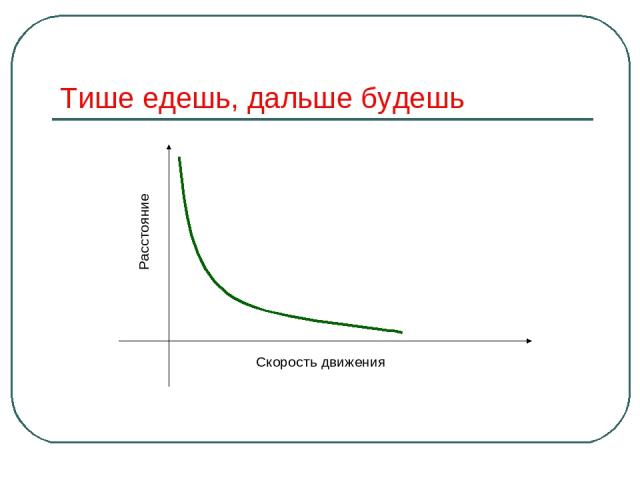
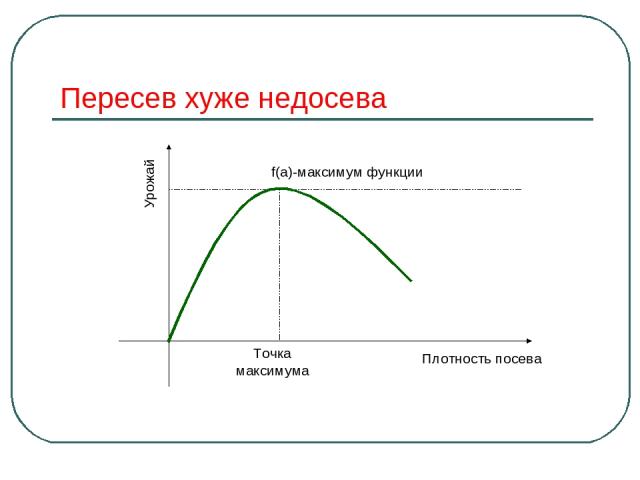
Прояви смекалку Чем дальше в лес, тем больше дров. Выше меры конь не скачет. Тише едешь, дальше будешь. Пересев хуже недосева. Пословицы – это отражение устойчивых закономерностей, выверенных многовековым опытом.

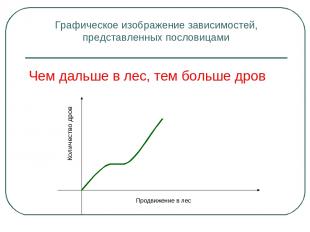
Графическое изображение зависимостей, представленных пословицами Чем дальше в лес, тем больше дров Продвижение в лес Количество дров

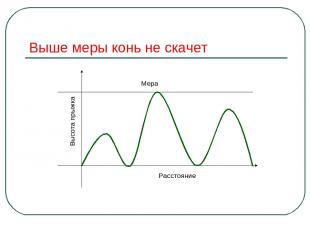
Выше меры конь не скачет Расстояние Мера Высота прыжка

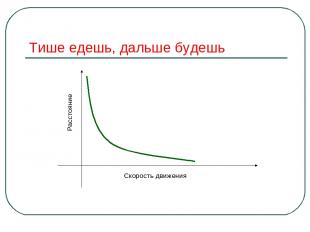
Тише едешь, дальше будешь Скорость движения Расстояние

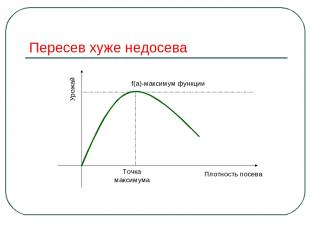
Пересев хуже недосева Точка максимума f(a)-максимум функции Плотность посева Урожай

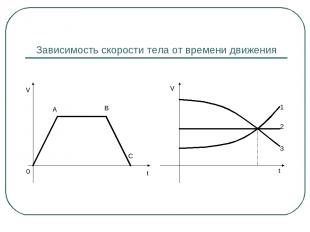
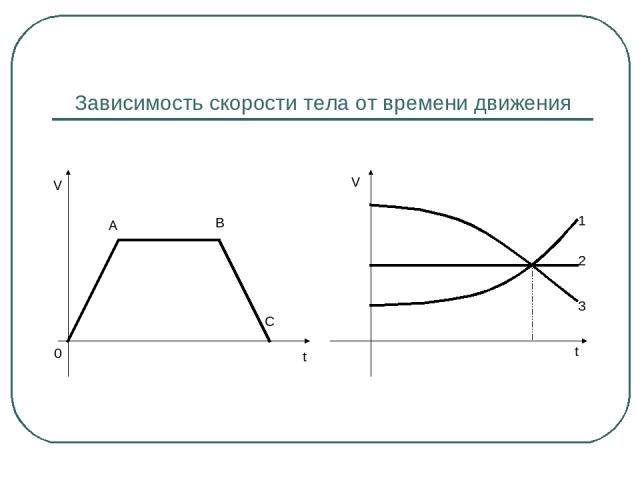
Зависимость скорости тела от времени движения 0 А В С V t 1 2 3 t V

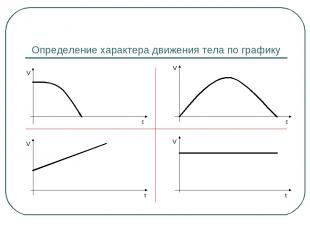
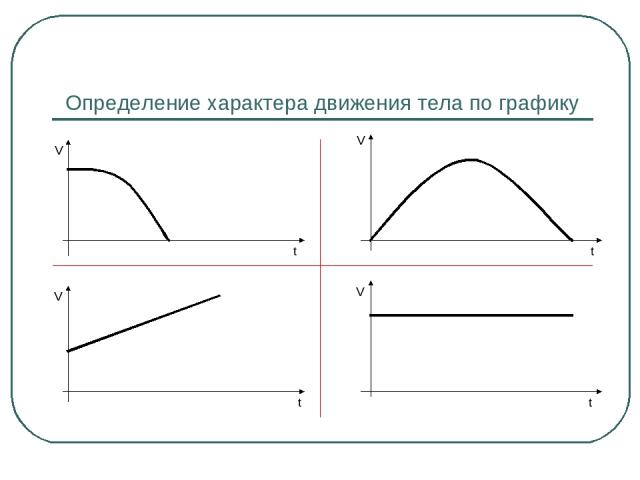
Определение характера движения тела по графику t V V t V t V t