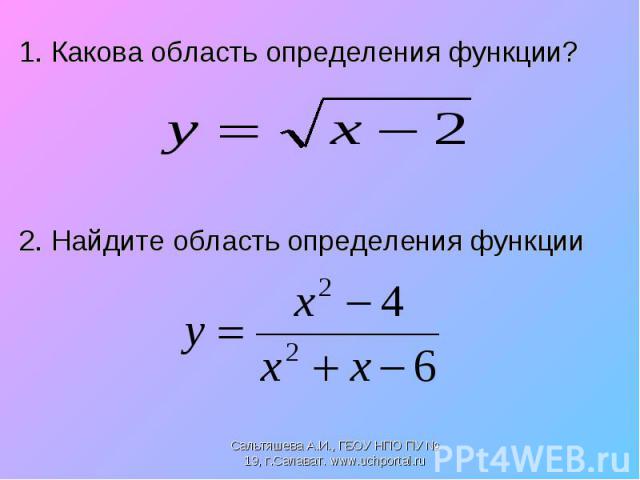Презентация на тему: Исследование функции с помощью производной

Достаточный признак возрастания функции. Достаточный признак возрастания функции. Достаточный признак убывания функции. Какие точки области определения функции являются критическими точками. Необходимое условие экстремума (или теорема французского математика – теорема Ферма) Какая точка называется точкой максимума? (упрощенная формулировка этого признака). Какая точка называется точкой минимума? (упрощенная формулировка этого признака)

Если функция f Если функция f имеет неотрицательную производную в каждой точке интервала (а;b), то функция f возрастает на интервале (а;b).

Если функция f Если функция f имеет неположительную производную в каждой точке интервала (а;b), то функция f убывает на интервале (а;b).

Если точка х0 является точкой экстремума функции f и в этой точке существует производная f `(x), то она равна нулю: f `(x) = 0. Если точка х0 является точкой экстремума функции f и в этой точке существует производная f `(x), то она равна нулю: f `(x) = 0.

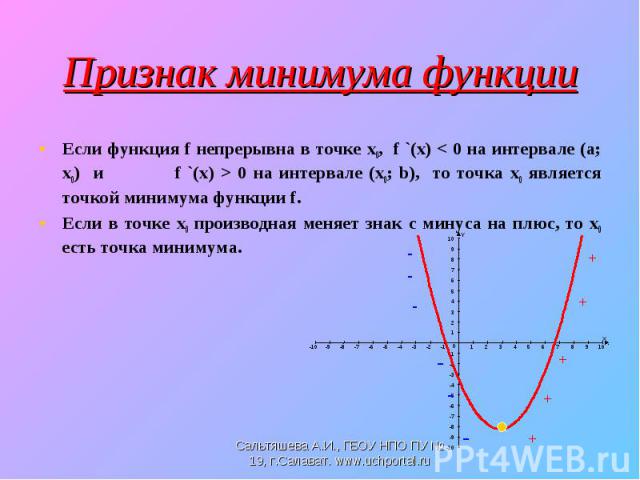
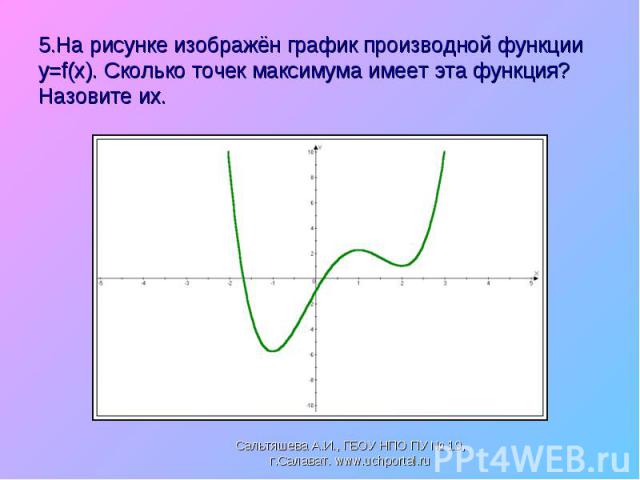
Если функция f непрерывна в точке х0, а f `(x) > 0 на интервале (а; х0), и f `(x) < 0 на интервале (х0; b), то точка х0 является точкой максимума функции f. Если функция f непрерывна в точке х0, а f `(x) > 0 на интервале (а; х0), и f `(x) < 0 на интервале (х0; b), то точка х0 является точкой максимума функции f. Если в точке х0 производная меняет знак с плюса на минус, то точка х0 максимума.

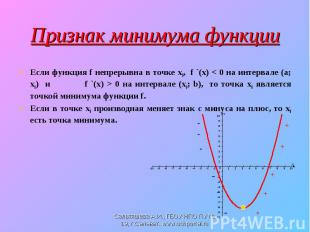
Если функция f непрерывна в точке х0, f `(x) < 0 на интервале (а; х0) и f `(x) > 0 на интервале (х0; b), то точка х0 является точкой минимума функции f. Если функция f непрерывна в точке х0, f `(x) < 0 на интервале (а; х0) и f `(x) > 0 на интервале (х0; b), то точка х0 является точкой минимума функции f. Если в точке х0 производная меняет знак с минуса на плюс, то х0 есть точка минимума.

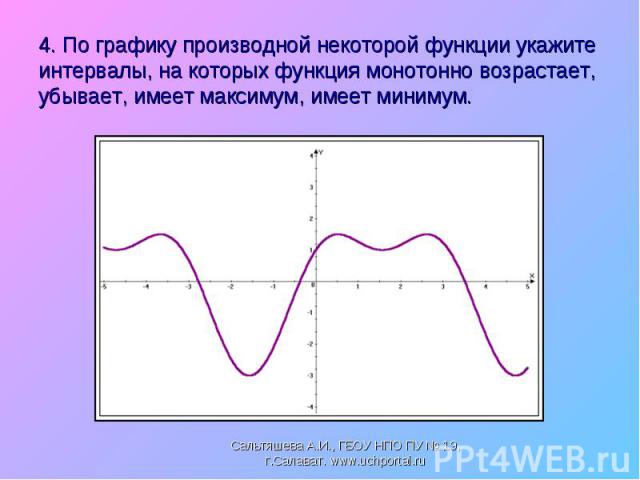
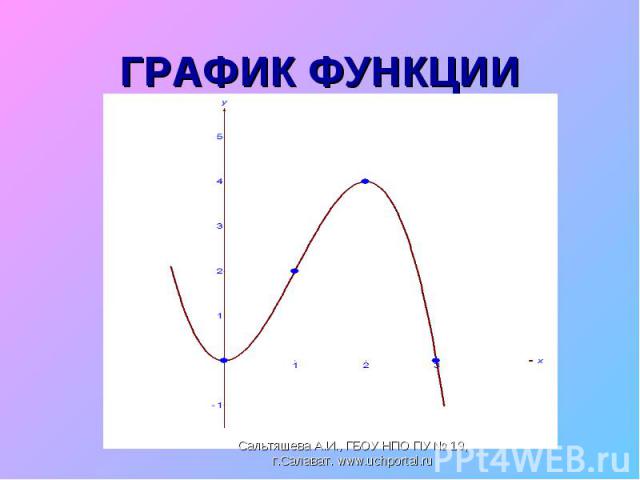
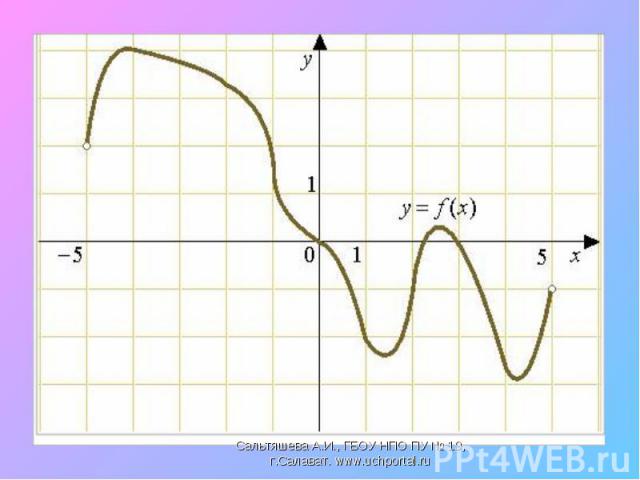
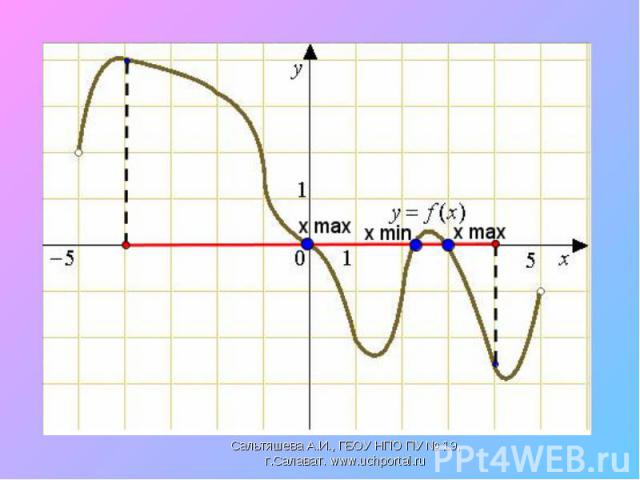
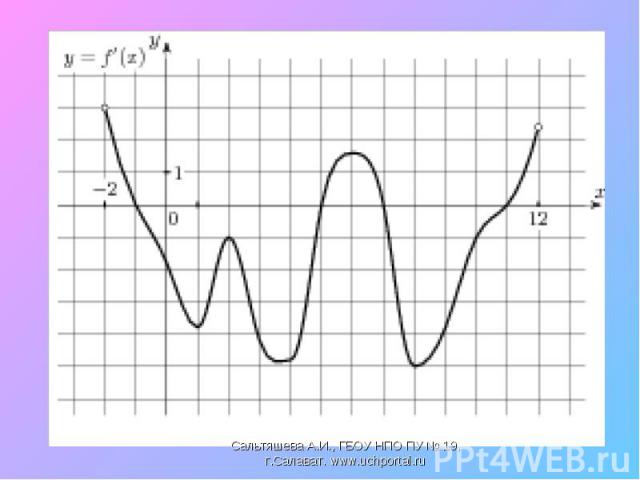
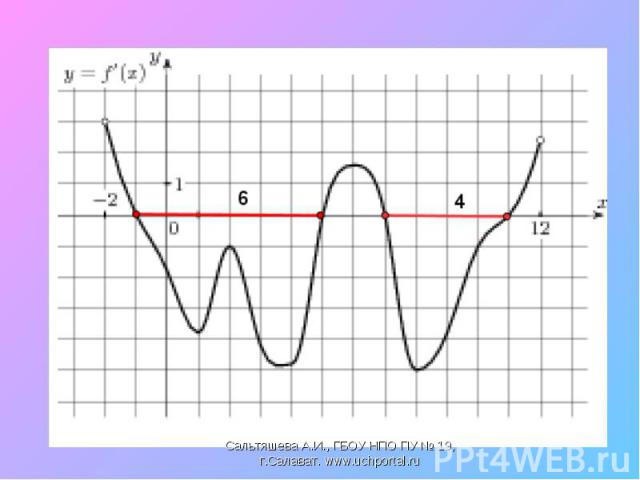
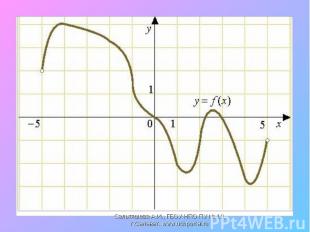
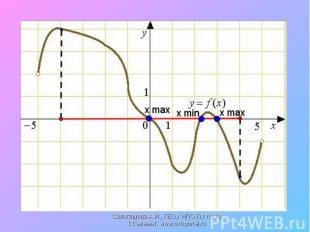
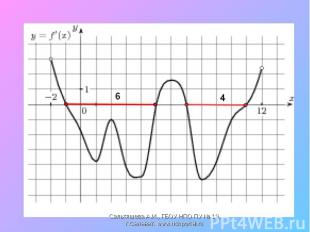
Найти промежутки возрастания и убывания функции, точки экстремума Найти промежутки возрастания и убывания функции, точки экстремума

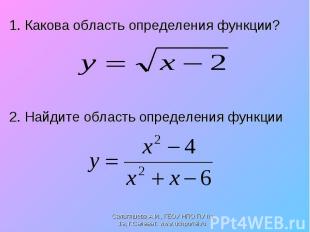
1. Какова область определения функции? 1. Какова область определения функции? 2. Найдите область определения функции

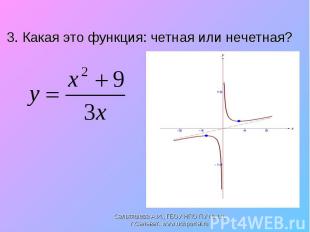
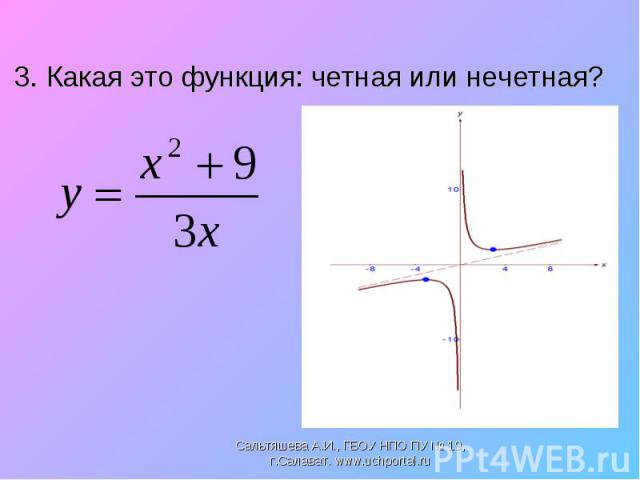
3. Какая это функция: четная или нечетная?

ЛЕОНАРД ЭЙЛЕР ЛЕОНАРД ЭЙЛЕР (1707-1783) Математик, механик, физик и астроном. По происхождению швейцарец. В 1726 был приглашен в Петербургскую академию наук и переехал в 1727 в Россию.

Найти область определения функции. (Указать множество значений переменной х, при которых данная функция определена). Найти область определения функции. (Указать множество значений переменной х, при которых данная функция определена). Исследовать функцию на четность. (Выяснить, симметрична ли область определения функции относительно начала координат и найти y = f(-x). Если f(-x) = f(x), то функция четная, если y f(-x) = -f(x), то функция нечетная). Найти нули функции. (Точки пересечения с осями координат). Исследовать функцию на монотонность. (Если f ’(x) > 0, то функция возрастает, если f ’(x) < 0, то функция убывает). Записать точки экстремума и экстремумы функции. (Найти значение функции в точках экстремума). Дополнительные точки. Построение графика.

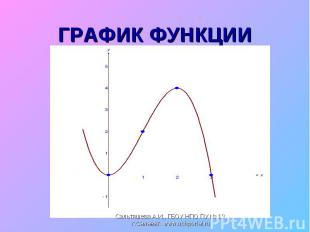
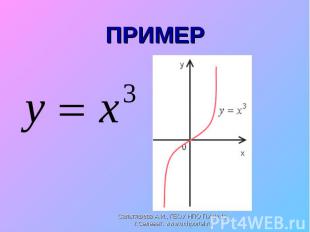
Исследовать функцию и построить график Исследовать функцию и построить график

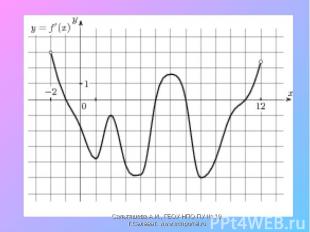
1. № 300 (а, б). 1. № 300 (а, б). 2. Нестандартное задание: найдите функции, описывающие реальные физические процессы, которые вы изучали на уроках физики и исследуйте их.

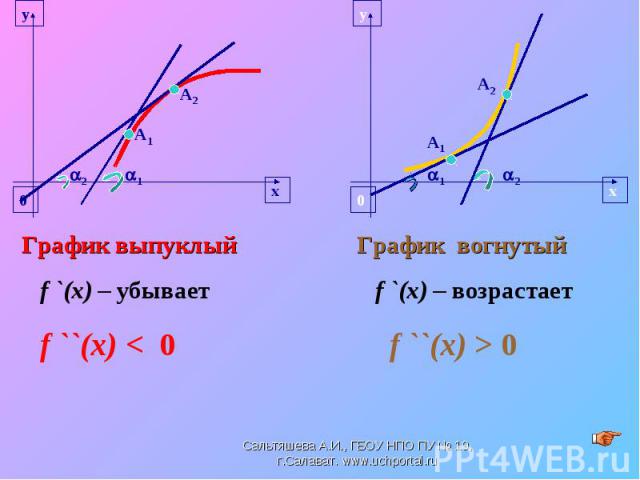
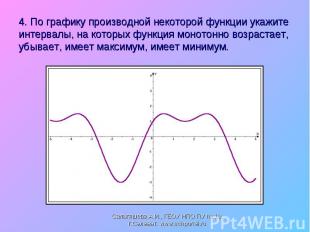
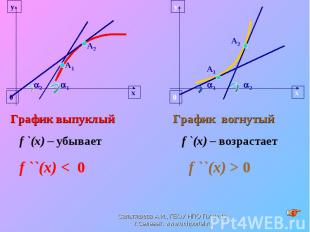
Рассмотрите взаимосвязь между свойством функции и производной. Как влияет знак второй производной на выпуклость функции. Рассмотрите взаимосвязь между свойством функции и производной. Как влияет знак второй производной на выпуклость функции. Выставление оценок за фронтальный опрос, за блиц-опрос и за практическую работу у доски. Будьте добры, покажите, пожалуйста, ваше настроение в конце нашего урока.