Презентация на тему: Решение квадратных уравнений с применением циркуля и линейки

Решение квадратных уравнений с применением циркуля и линейки Выполнил...

Корни квадратного уравнения ах²+bx+c=0 (а≠0) можно рассматривать как абсциссы точек пересечения окружности с центром Q, проходящей через точку А(0;1), и оси Ох.Решение уравнения сводится к построению на координатной плоскости окружности с центром Q и радиусом QA (для этого и понадобятся инструменты) и определению абсцисс точек пересечения окружности с осью Ох.Возможны 3 случая:

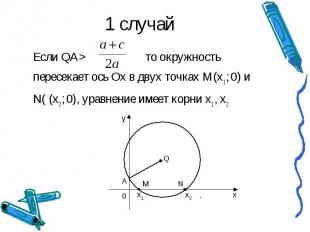
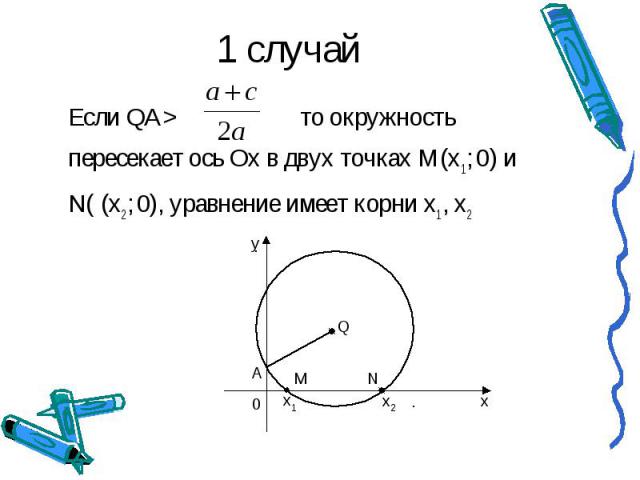
1 случай Если QA>то окружность пересекает ось Ох в двух точках М(х1 ; 0) и N( (х2 ; 0), уравнение имеет корни х1 , х2

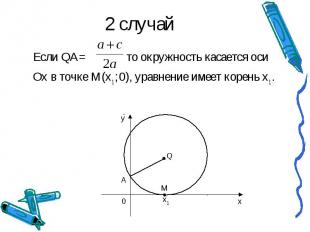
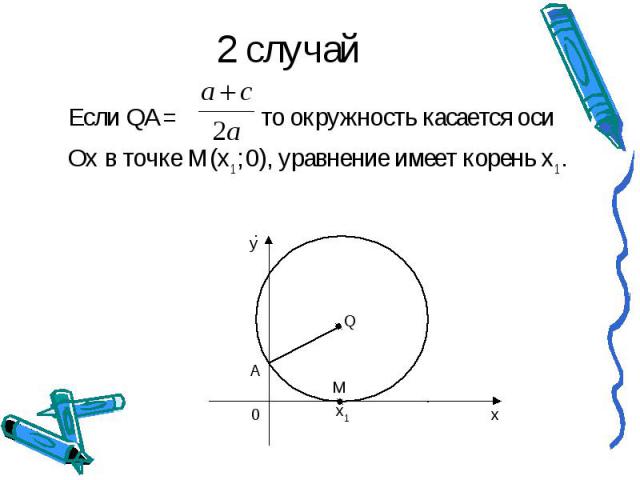
2 случай Если QA= то окружность касается оси Ох в точке М(х1 ; 0), уравнение имеет корень х1 .

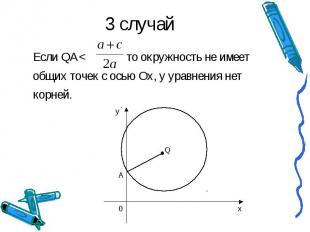
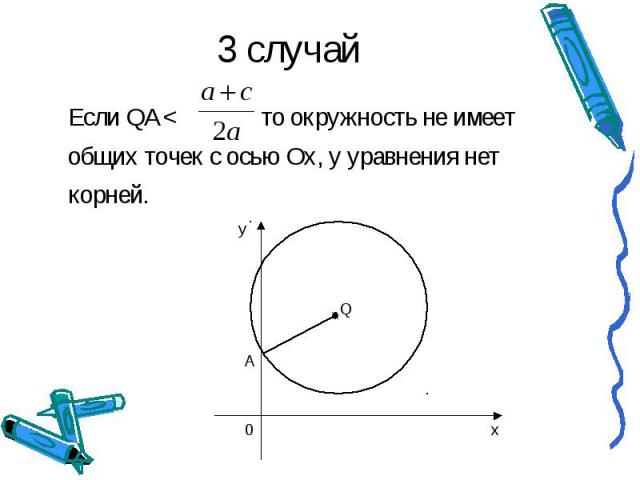
3 случай Если QA< то окружность не имеет общих точек с осью Ох, у уравнения нет корней.

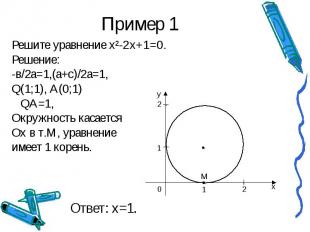
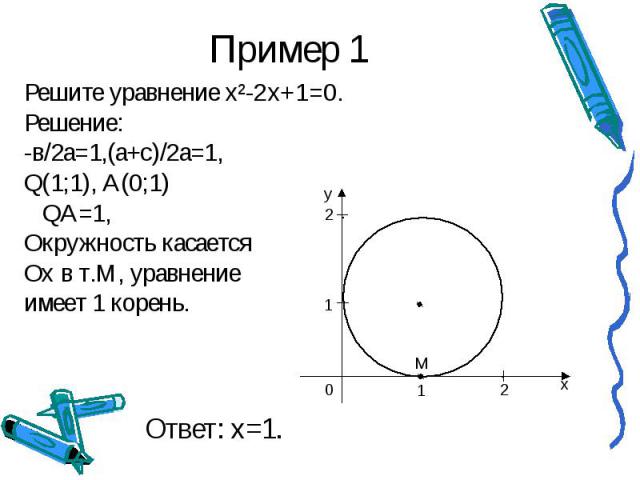
Пример 1 Решите уравнение х²-2x+1=0.Решение:-в/2а=1,(а+с)/2а=1,Q(1;1), А(0;1) QА=1,Окружность касаетсяОх в т.М, уравнение имеет 1 корень.

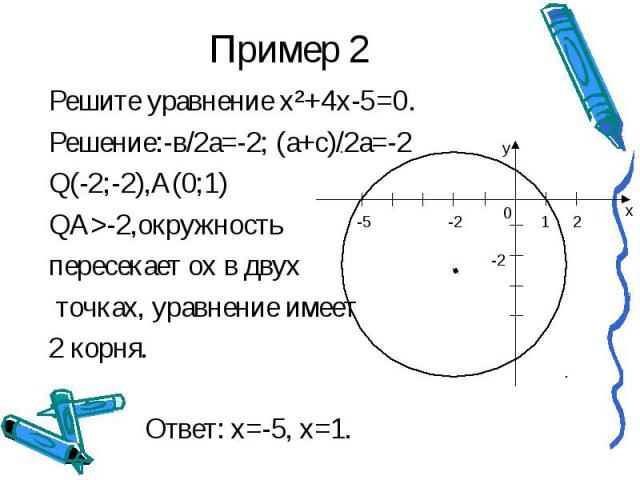
Пример 2 Решите уравнение х²+4x-5=0.Решение:-в/2а=-2; (а+с)/2а=-2Q(-2;-2),А(0;1)QА>-2,окружностьпересекает ох в двух точках, уравнение имеет 2 корня.

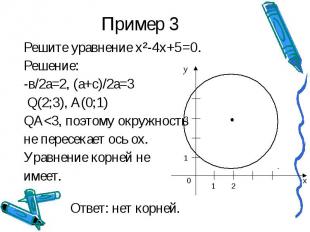
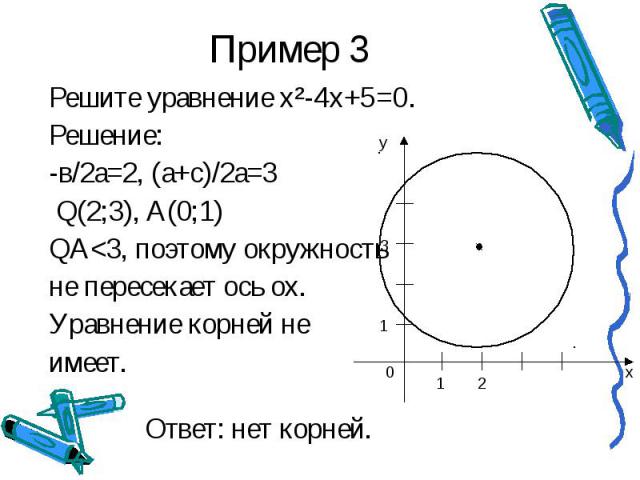
Пример 3 Решите уравнение х²-4x+5=0.Решение:-в/2а=2, (а+с)/2а=3 Q(2;3), А(0;1)QА<3, поэтому окружностьне пересекает ось ох.Уравнение корней не имеет.

Замечание Конечно, решать уравнения по формуле проще, чем выполнять построения. Но нам сейчас интересно отметить важный факт: квадратные уравнения могут быть решены с привлечением геометрии. Правда, этот способ не позволяет получать точные решения в случае произвольных коэффициентов уравнения.

Благодаримза внимание.