Презентация на тему: Построение графиков функций, содержащих знак модуля

Построение графиков функций, содержащих знак модуля Научно-исследовательский проект.Автор проекта:Гребень Юлия Алексеевнаучащаяся 10 «А» классаМОУ гимназии №40Г. КраснодараНаучный руководитель –учитель математики,МОУ гимназии №40г. КраснодараШмитько Ирина Анатольевна2007-08 г.г.

I. Введение.I. Введение.II. Основная часть. 1) Понятия и определения. 2) Теоремы, следствия. 3) Построение графиков.III. Заключение.IV. Список используемой литературы.

Объект исследования – математика.Предмет исследования – функции, содержащие знак модуля.Проблема исследования: построение графиков функций, содержащих модуль.Цель исследования: получение более широких знаний о модуле числа, различных способах решения уравнений, содержащих знак абсолютной величины.Задача исследования: использование различных методов исследования (теоретический, практический, исследовательский), расширение познавательного интереса к изучению алгебры, углубление знаний по теории модуля и решение задач, выходящих за страницы школьных учебников.

Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово, которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках.В архитектуре - это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов.В технике - это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и т.п.Модуль объемного сжатия (в физике) - отношение нормального напряжения в материале к относительному удлинению.

II. Основная часть.Понятия и определения. Чтобы глубоко изучать данную тему, необходимо познакомиться с простейшими определениями, которые мне будут необходимы:Уравнение - это равенство, содержащее переменные.Уравнение с модулем - это уравнение, содержащее переменную под знаком абсолютной величины (под знаком модуля). Например: |x|=1Решить уравнение - это значит, найти все его корни, или доказать, что корней нет.В математике модуль имеет несколько значений, но в моей исследовательской работе я возьму лишь одно из них.Модулем или иначе абсолютной величиной отрицательного числа называется противоположное ему положительное число, модулем положительного числа и числа ноль называется само это число.

Теорема 1. Абсолютная величина действительного числа a≠0 равна большему из двух чисел a или -a.Следствие 1. Из теоремы следует, что |-a|=|a|. Следствие 2. Для любого действительного числа a справедливы неравенства a≤|a| , -a≤|a|Объединяя последние два неравенства в одно, получаем: -|a|≤a≤|a|

Теорема 2. Абсолютная величина любого действительного числа a равна арифметическому квадратному корню из a2 : |a|=√a2Эта теорема дает возможность при решении некоторых задач заменять |a| на √a2Геометрически |a| означает расстояние на координатной прямой от точки, изображающей число a, до начала отсчета.Если a≠0 то на координатной прямой существует две точки a и -a, равноудаленной от нуля, модули которых равны.Если a = 0, то на координатной прямой |a| изображается точкой 0.

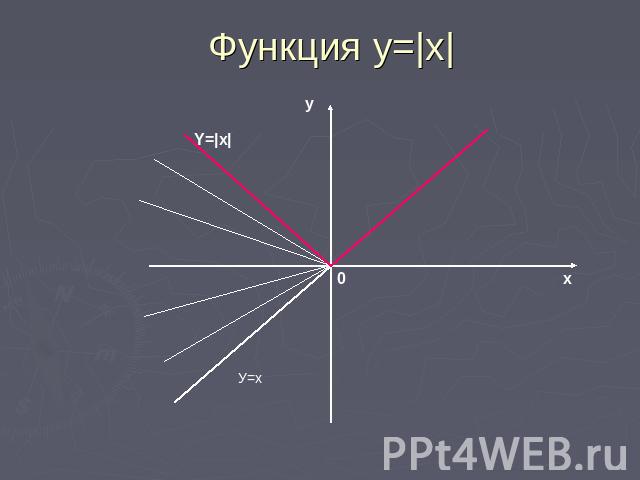
Функция у =|х| График функции у =|х| получается из графика у=х следующим образом: часть графика у=х, лежащая над осью х, сохраняется, часть его, лежащая ниже оси х , отображается симметрично относительно оси х.

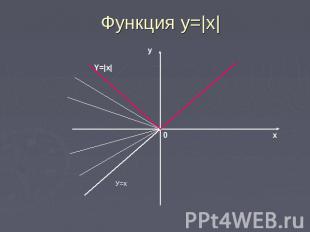
Функция у=|x|

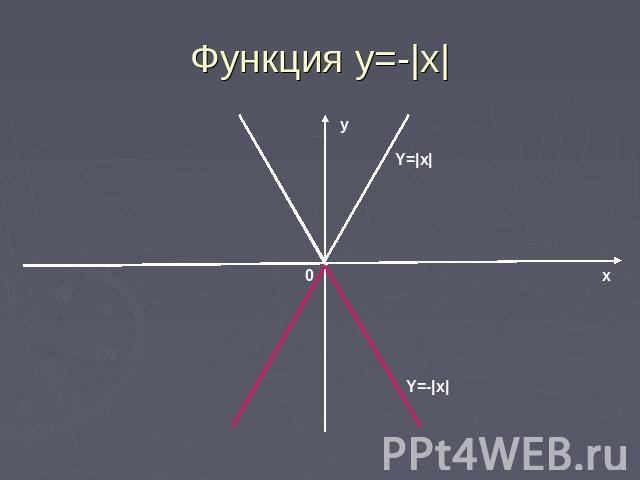
Функция y=-|x|График функции y=-|x| получается симметричным отображением графика y=|x| относительно оси х.

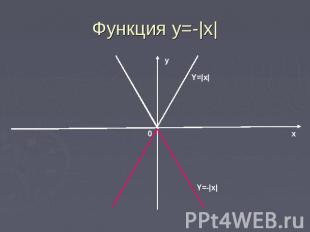
Функция у=-|x|

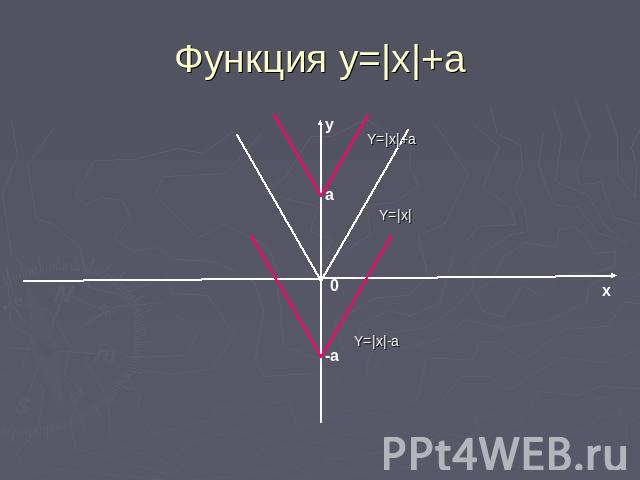
Функция у=|х|+а График функции у=|х|+а получается параллельным переносом графика у=|х| в положительном направлении оси у на а единицу отрезка при а>0 и в отрицательном направлении на |а| при а<0.

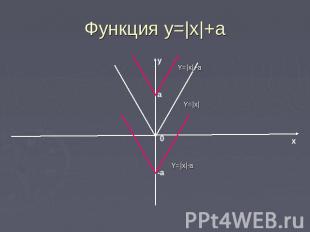
Функция у=|x|+a

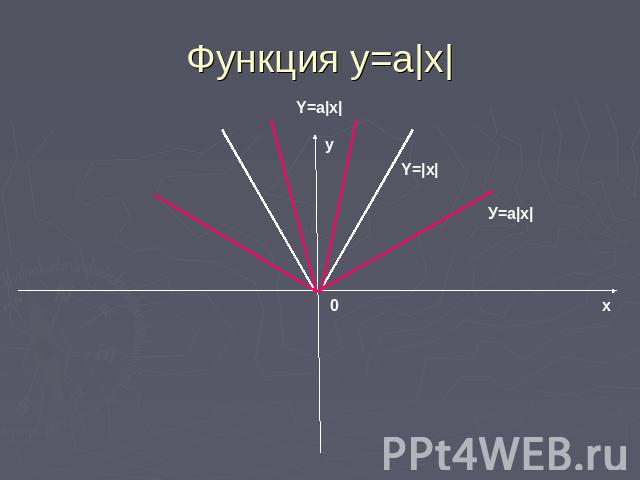
Функция у=а|х|График функции у=а|х| получается растяжением графика у=|х| вдоль оси у в а раз при а&gt;1 и сжатием вдоль этой оси в 1\а раз при 0&lt;a&lt;1.

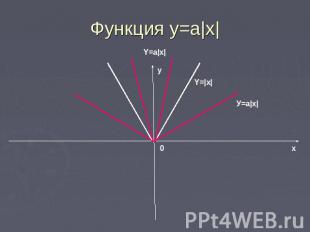
Функция y=a|x|

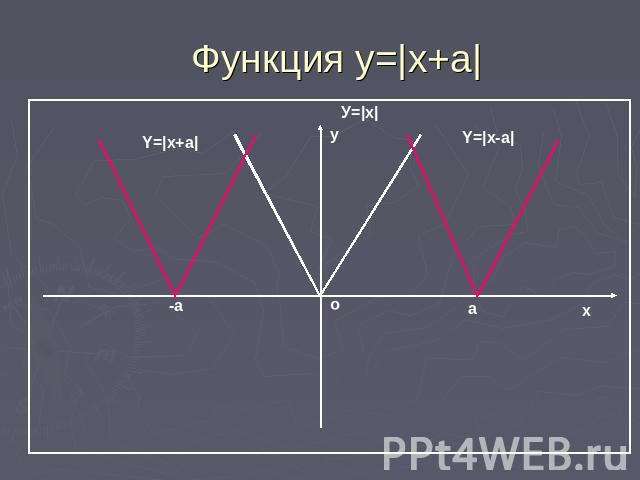
Функция у=|x+a| График функции у=|x+a| получается параллельным переносом графика y=|x| в отрицательном направлении от оси х на |x| при а>0 и в положительном направлении на |a| при a<0.

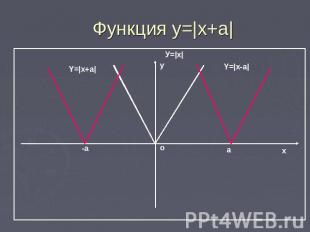
Функция y=|x+a|

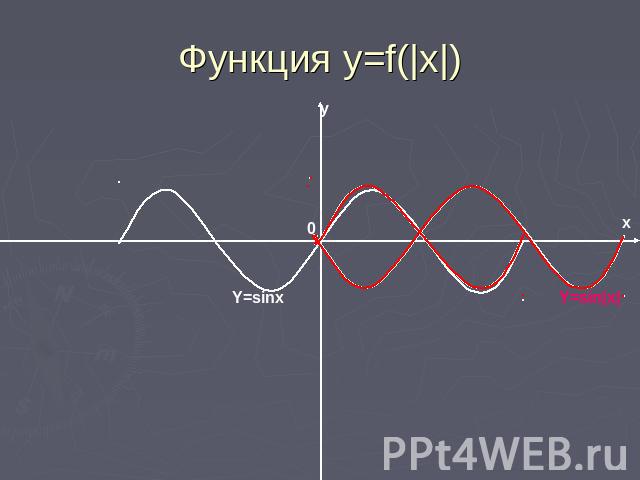
Функция y=f(|x|) График функции y=f(|x|) получается из графика y=f(x) следующим образом:1) при х>0 график f(x) сохраняется, 2) при x<0, полученная часть графика отображается симметрично относительно оси у.

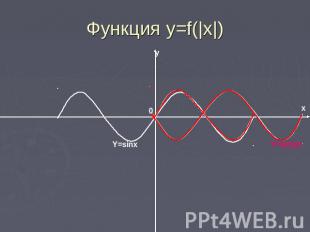
Функция y=f(|x|)

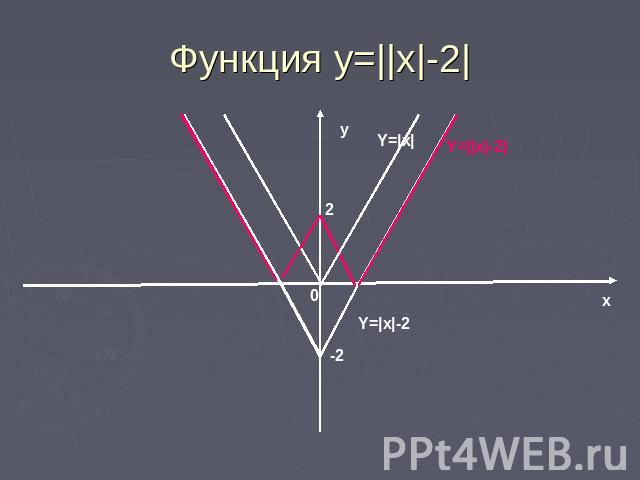
От теории к практике Рассмотрим построение более сложных графиков.Построить график функции у=||x|+2|.Построение. 1) Строим график y=|x|2)Смещаем его по оси у вниз на 2 ед.отр.3)Отображаем часть графика, расположенного под осью х, симметрично этой оси, в верхнюю полуплоскость.

Функция у=||x|-2|

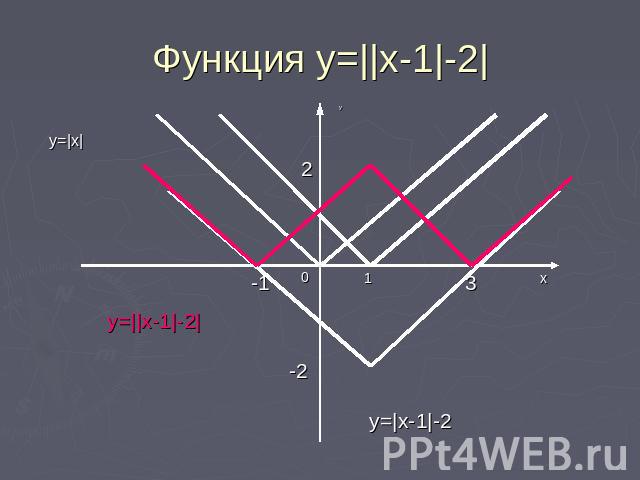
Функция y=||x-1|-2| Построение.1)Строим график функции y=|x|.2)Строим график функции y=|x-1|.3)Строим график функции y= |x-1|-2.4)Применяем к графику y=|x-1|-2 операцию “модуль”.

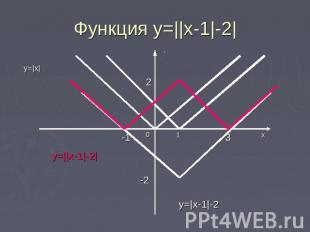
Функция y=||x-1|-2|x

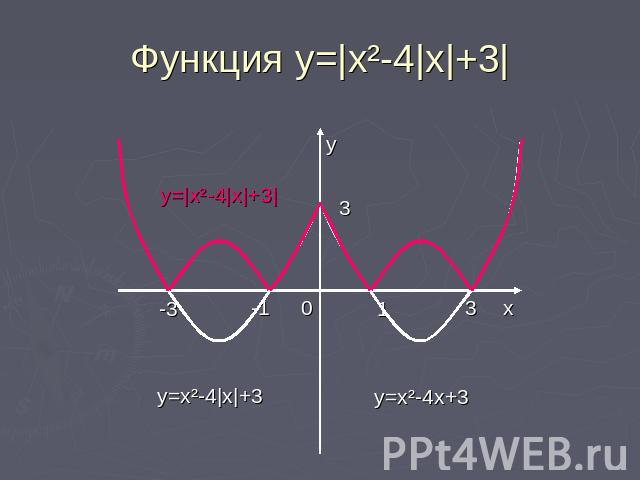
Функция y=|x²-4|x|-3| Построение.1)Строим график y=x²-4x+32)y=x²-4|x|+3 — отражаем полученный график в п.1 относительно оси ординат. Функция чётная.3)y=|x²-4|x|+3| — часть графика, расположенную в нижней полу плоскости, отражаем относительно оси абсцисс. Полученная в верхней полуплоскости линия и будет графиком заданной функции.

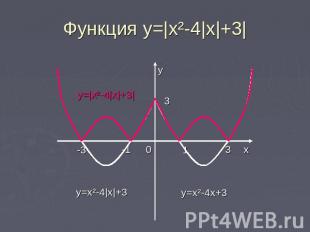
Функция y=|x²-4|x|+3|

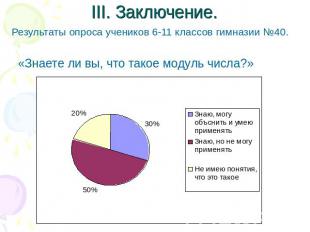
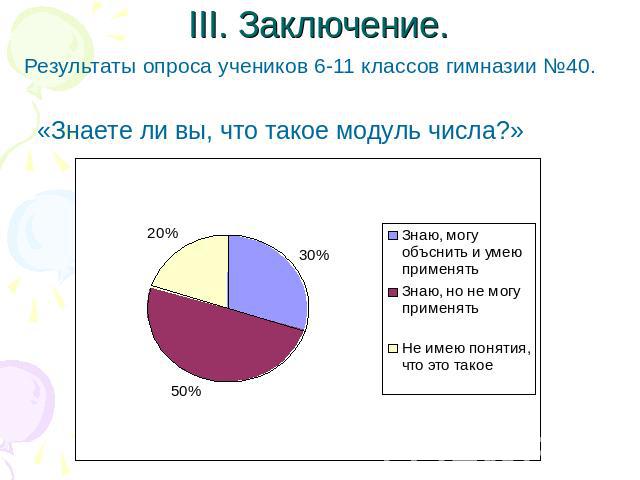
III. Заключение. Результаты опроса учеников 6-11 классов гимназии №40. «Знаете ли вы, что такое модуль числа?»

Мой научно-исследовательский проект можно использовать:1) на уроках алгебры в 7-9 классах;2) для индивидуального изучения понятия темы «модуль числа»;3) групповых и факультативных занятиях;4) для подготовки к экзаменам.

Мой научно-исследовательский проект будет полезен в работе: ученикам учителям. Он поможет отыскать новые пути совершенствования обычного школьного урока.

Список литературы. Детская энциклопедия. М., «Педагогика», 1990.Глейзер Г. И. История математики в школе. М. «Просвещение», 1982.Дынкин Е.Б., Молчанова С.А. Математические задачи. М., «Наука», 1993.Петраков И.С. Математические кружки в 8-10 классах. М., «Просвещение», 1987.Талочкин П.Б. Неравенства и уравнения. М., «Просвещение», 1989. Башмаков М.И. Уравнения и неравенства. Издательство Московского университета, 1974.