Презентация на тему: Последовательности и Династия Романовых

последовательности и Династия Романовых Выполнила:Досалиева Н., учащаяся 9 классаРуководитель:Елисеева Г. И., учитель математики

Определение числовой последовательности Числовая последовательность - множество чисел с указанным способом нумерации.Если последовательность содержит конечное число членов, то она называется конечной последовательностью, а если бесконечное число членов - бесконечной.

Арифметическая прогрессия Арифметическая прогрессия-последовательность (an), каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом. an =an+1+d , где d - некоторое число.Например: 1; 5; 9; 13; 17;… d=4

Последовательность Фибоначчи Последовательность Фибоначчи – это числовая последовательность, в которой каждый член, начиная с третьего, равен сумме двух предыдущих членов. Пример: 1; 1; 2; 3; 5; 8; 13; 21;….

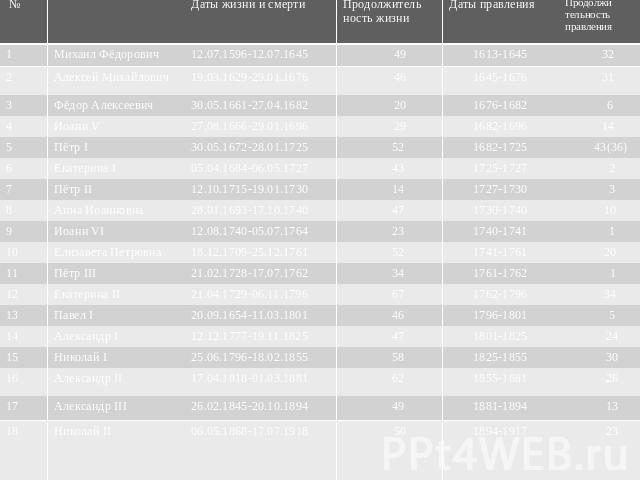
Исследовательская часть Числа, равные продолжительности правления каждого из династии Романовых: 32; 31; 6; 14; 36; 2; 3; 10; 1; 20; 1; 34; 5; 24; 30; 26; 13; 23.Запишем их в виде упорядоченного ряда:1; 1; 2; 3; 5; 6; 10; 13; 14; 20; 23; 24; 26; 30; 31; 32; 34; 36Числа, выделенные красным цветом, являются членами последовательности Фибоначчи.

Арифметические прогрессии Из чисел, равных продолжительности правления каждого из династии Романовых: 1; 1; 2; 3; 5; 6; 10; 13; 14; 20; 23; 24; 26; 30; 31; 32; 34; 36, можно составить следующие арифметические прогрессии:14; 20; 26; 32, где d=65; 14; 23; 32, где d=930; 32; 34; 46, где d=22; 6; 10; 14, где d=4

В полученных арифметических прогрессиях:14; 20; 26; 325; 14; 23; 3230; 32; 34; 362; 6; 10; 14обнаруживается, что количество членов во всех четырех прогрессиях равно четырем.

Также можно заметить: При исследовании этих чисел на наличие двузначных и однозначных чисел получаем, что двузначных чисел: во втором десятке – 3 числа (10; 13; 14)в третьем десятке – 4 числа (20; 23; 24; 26)в четвертом десятке – 5 чисел (30; 31; 32; 34; 36) однозначных чисел – 6 чисел (1; 1; 2; 3; 5; 6), т.е. их количества составляют последовательность: 3; 4; 5; 6, которая является арифметической прогрессией, где d = 1.

Исследование чисел, равных продолжительности жизни правителей из династии Романовых Числа, равные продолжительности жизни правителей из династии Романовых:  49; 46; 20; 29; 52; 43; 14; 47; 23; 52; 34; 67; 46; 47; 58; 62; 49; 50. Запишем числа в порядке возрастания: 14; 20; 23; 29; 34; 43; 46; 46; 47; 47; 49; 49; 50; 52; 52; 58; 62; 67.

Арифметические прогрессии Из чисел можно составить следующие арифметические прогрессии: 43; 46; 49; 52, где d=346; 52; 58, где d=649; 58; 67, где d=9Получаем: d=3, d=6, d=9, т.е. арифметическую прогрессию с разностью, равной 3.

Спасибо за внимание