Презентация на тему: Построение графиков функций сложных функций на основе свойств монотонности

Построение графиков функций сложных функций на основе свойств монотонности АВТОР проекта: Зародов Никита Евгеньевич, ученик 10-А класса МОУ «СОШ №21», г. Подольск, МОРУКОВОДИТЕЛЬ проекта: Буянова Анна Матвеевна, учитель математики МОУ «СОШ №21», г. Подольск, МО

гипотеза Графики сложных функций вида y=f (v (x)) легко построить, зная свойства основных элементарных функцийвида y=f (x). Выработаемпростой алгоритм построения графиков.

ДЛЯ ЭТОГО ВСПОМНИМ основные свойства функций 1. Область определения/область значения функций 2. Четность/нечетностьфункций 3. Монотонность функций
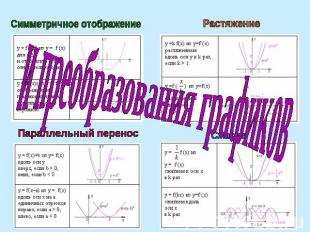
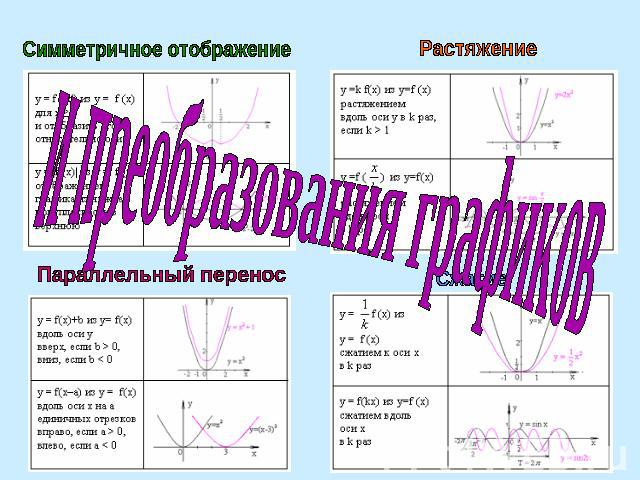
и преобразования графиков Симметричное отображение Параллельный перенос Растяжение

П Р И С Т У П И М к построению графиков сложных функцийвида y=f (v (x)).
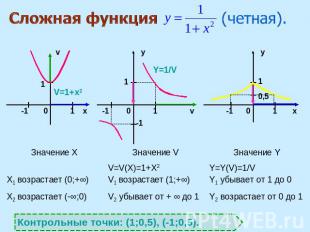
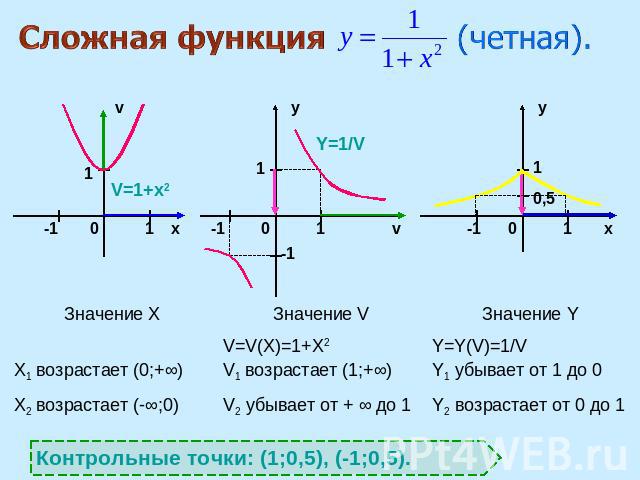
Сложная функция (четная). Контрольные точки: (1;0,5), (-1;0,5).
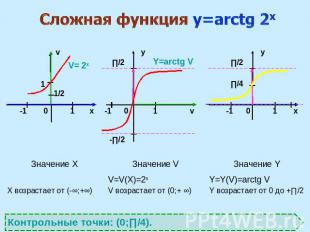
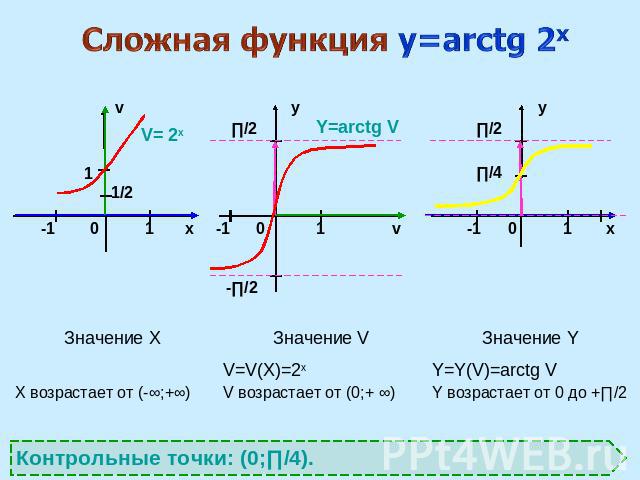
Сложная функция y=arctg 2x Контрольные точки: (0;∏/4).
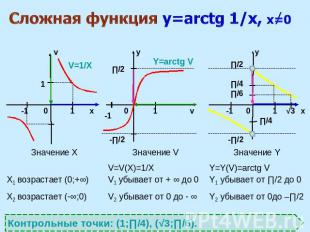
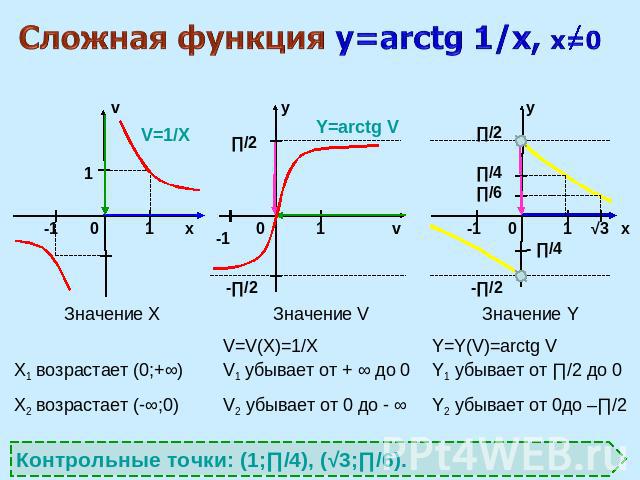
Сложная функция y=arctg 1/x, х=0 Контрольные точки: (1;∏/4), (√3;∏/6).
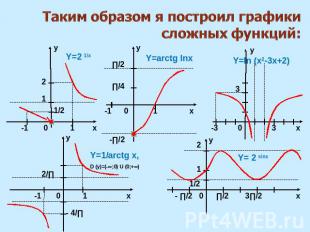
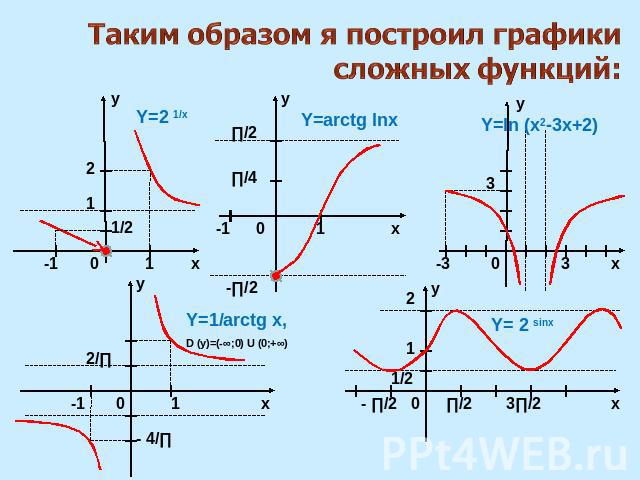
Таким образом я построил графики сложных функций:

И ВЫРАБОТАЛ АЛГОРИТМ 1. начертить графики внутренней v = v(x) и внешней y = f (v) функций и систему координат XOY. Алгоритм построенияграфиков сложных функций 3. определить промежутки монотонности внешней функции y = f(v). 4. на каждом промежутке определить границы изменения функции v = v(x) и выбрать те значения v (x), которые попадают в область определения функции y = f (v). 5. по графику внешней функции y = f (v) найти характер изменения функции y. 6. построить график сложной функции y = y (x) в системе координат XOY с учетом промежутков монотонности Х, Y и контрольных точек.
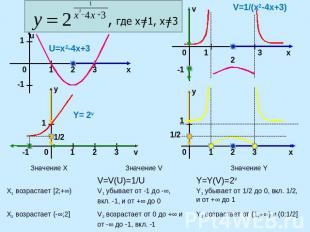
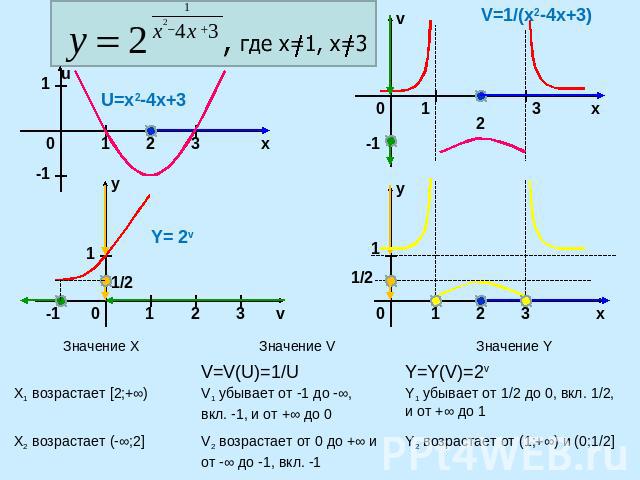
V=1/(x2-4x+3)
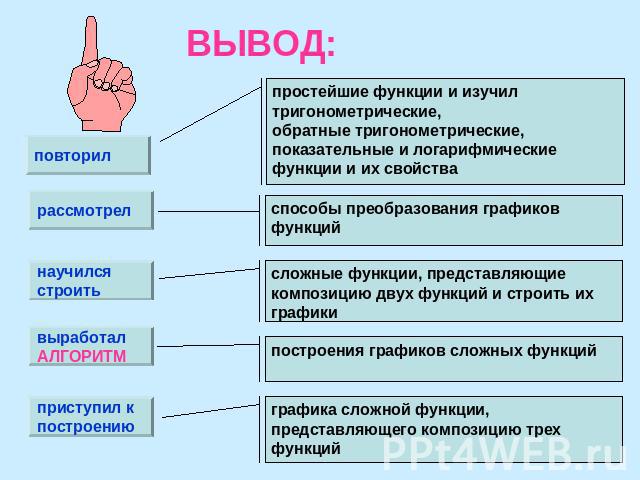
ВЫВОД: повторил рассмотрел научилсястроить выработалАЛГОРИТМ приступил кпостроению простейшие функции и изучилтригонометрические,обратные тригонометрические, показательные и логарифмическиефункции и их свойства способы преобразования графиков функций сложные функции, представляющие композицию двух функций и строить их графики построения графиков сложных функций графика сложной функции, представляющего композицию трех функций