Презентация на тему: Построение графиков сложных функций

«Построение графиков сложных функций»Попова Лариса Анатольевна №238-127-765

Цели урока: образовательная: закрепить знания по формированию массивов данных в табличной форме, отработать навык построения диаграмм при построении графиков;развивающая: познакомить со сложными графиками, развивать алгоритмическое мышление; умение применять полученные знания при решении задач; умение рассуждать; развивать познавательный интерес; познакомить со сложными графиками;воспитательная: прививать учащимся навык самостоятельности в работе, воспитывать трудолюбие, чувство уважения к науке.

Назначение электронных таблиц, применение в каких отраслях жизни?Перечислите основные функции электронных таблиц.Что такое диаграмма и какие действия можно с ней?Назовите основные типы диаграмм?Как связана таблица и построенная диаграмма?Какими способами можно включить Мастер диаграмм? Какие основные типы ссылок вы знаете? Назовите различия между относительными и абсолютными ссылками проявляются при копировании формулы из активной ячейки в другую ячейку? 

Параболоиды в мире В техникеПараболоид вращения фокусирует пучок лучей,параллельный главной оси, в одну точкуЧасто используется свойство параболоида вращения собирать пучок лучей, параллельный главной оси, в одну точку — фокус, или, наоборот, формировать параллельный пучок излучения от находящегося в фокусе источника. На этом принципе основаны параболические антенны, телескопы-рефлекторы, прожекторы, автомобильные фары и т.д.В литературеУстройство, описанное в романе А. Н. Толстого «Гиперболоид инженера Гарина», должно было быть параболоидом

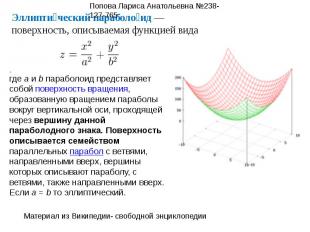
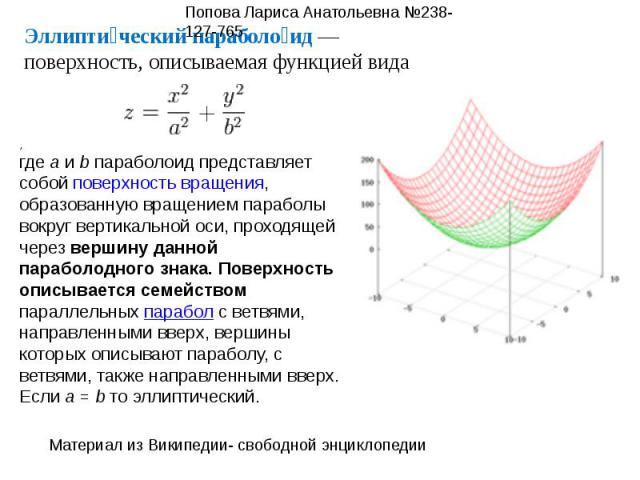
,где a и b параболоид представляет собой поверхность вращения, образованную вращением параболы вокруг вертикальной оси, проходящей через вершину данной параболодного знака. Поверхность описывается семейством параллельных парабол с ветвями, направленными вверх, вершины которых описывают параболу, с ветвями, также направленными вверх.Если a = b то эллиптический.Эллиптический параболоид — поверхность, описываемая функцией вида

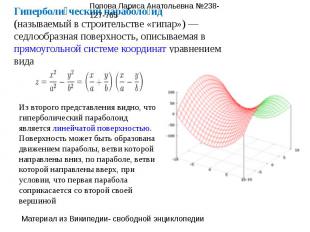
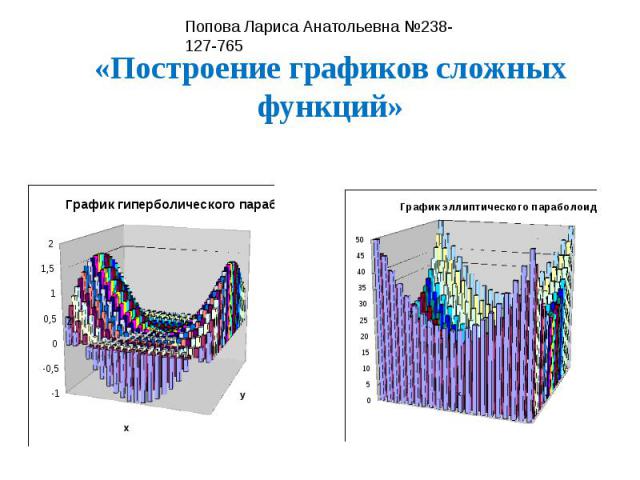
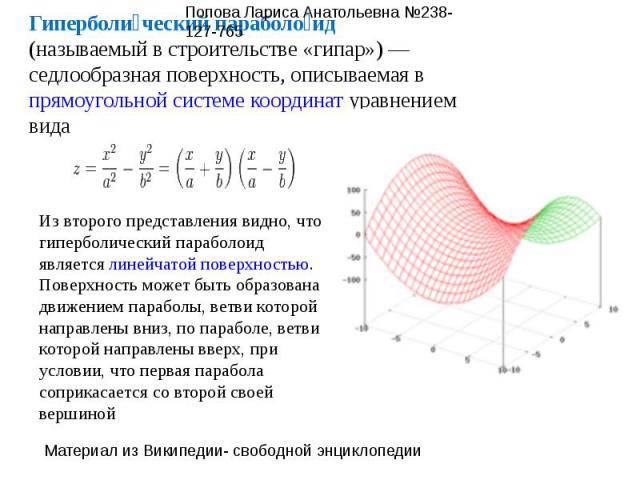
Гиперболический параболоид (называемый в строительстве «гипар») — седлообразная поверхность, описываемая в прямоугольной системе координат уравнением видаИз второго представления видно, что гиперболический параболоид является линейчатой поверхностью.Поверхность может быть образована движением параболы, ветви которой направлены вниз, по параболе, ветви которой направлены вверх, при условии, что первая парабола соприкасается со второй своей вершиной

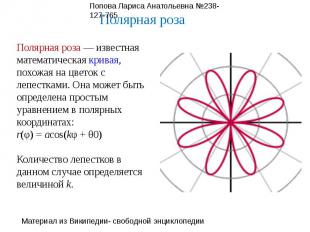
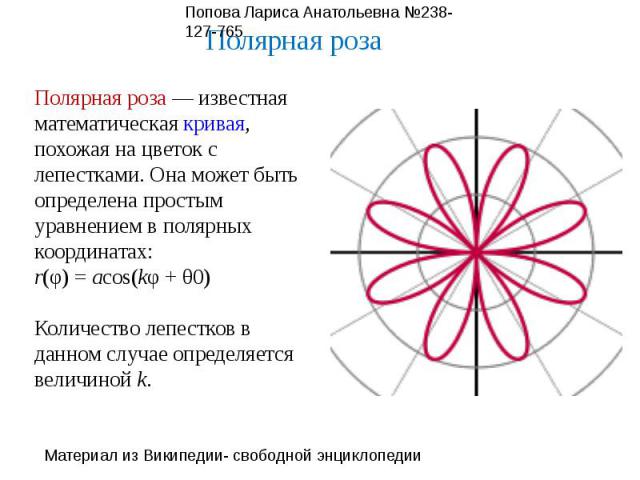
Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах:r(φ) = acos(kφ + θ0)Количество лепестков в данном случае определяется величиной k.

КардиоидаУравнение

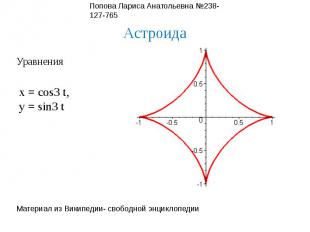
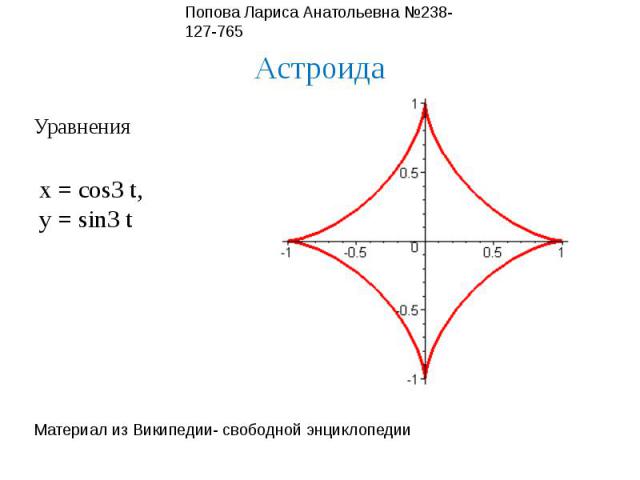
АстроидаУравненияx = cos3 t,y = sin3 t

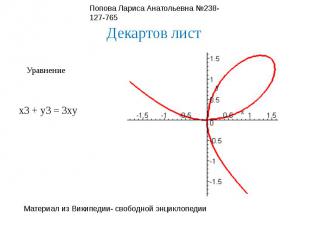
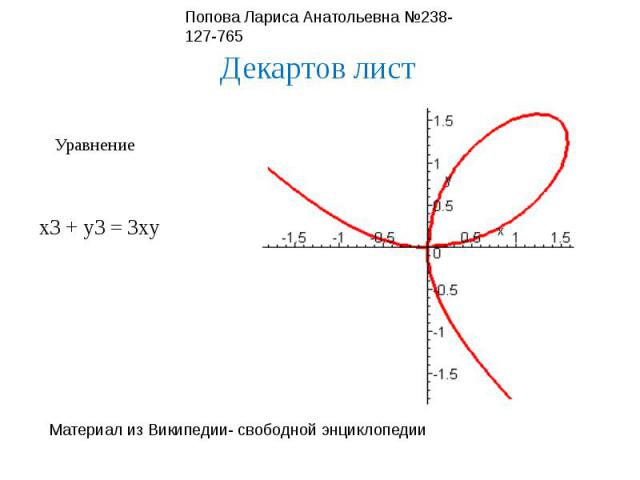
Декартов листУравнениеx3 + y3 = 3xy

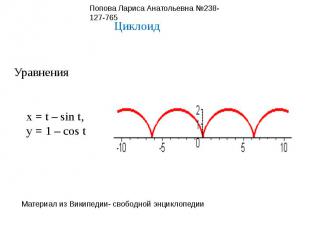
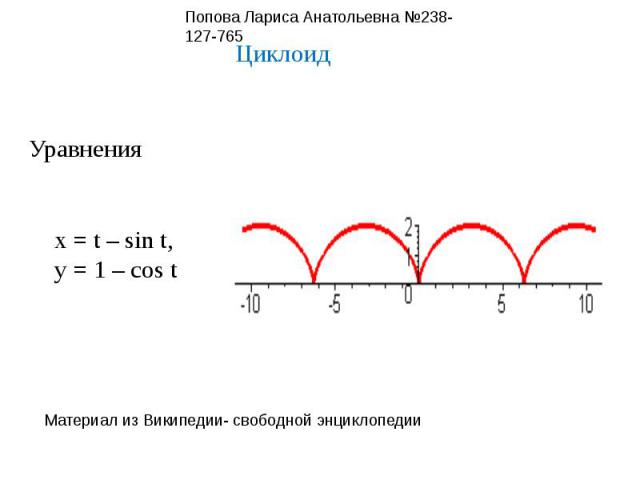
ЦиклоидУравненияx = t – sin t,y = 1 – cos t

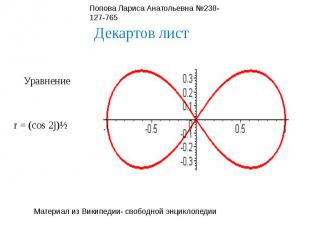
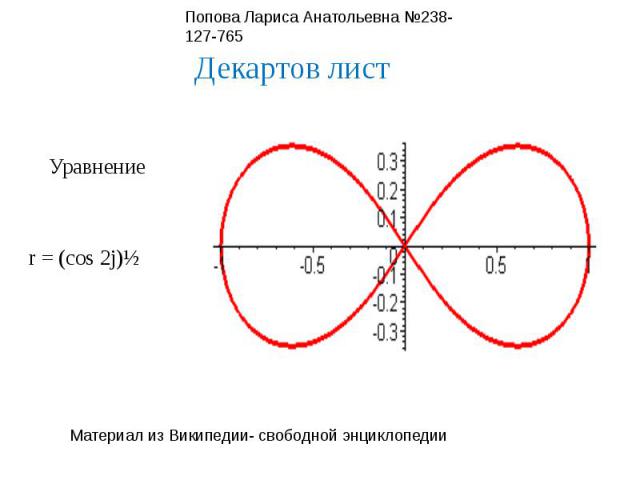
Декартов листУравнениеr = (cos 2j)½

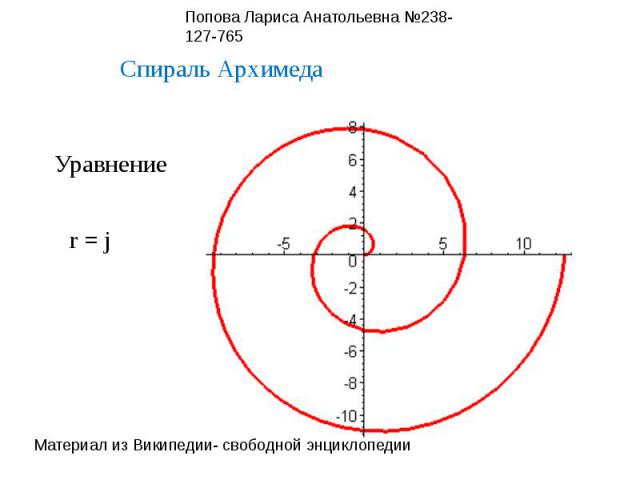
УравнениеСпираль Архимедаr = j

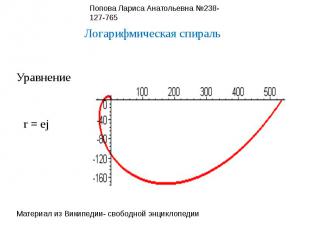
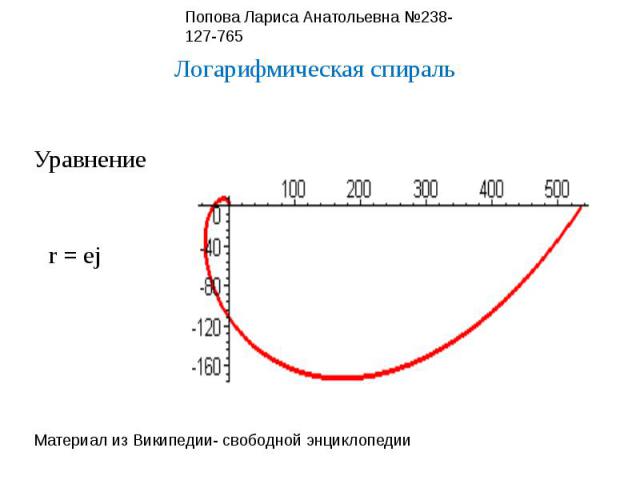
Логарифмическая спиральУравнениеr = ej