Презентация на тему: История систем счисления

история (системы счисления) Плотникова Надежда Михайловна Плотников Виктор Егорович

Очарование, сопровождающее науку, может победить свойственное людям отвращение к  напряжению ума.  Гаспа р Монж, граф де Пелю з (10.5.1746-28.7.1818) — французский математик, геометр, государственный деятель, морской министр.

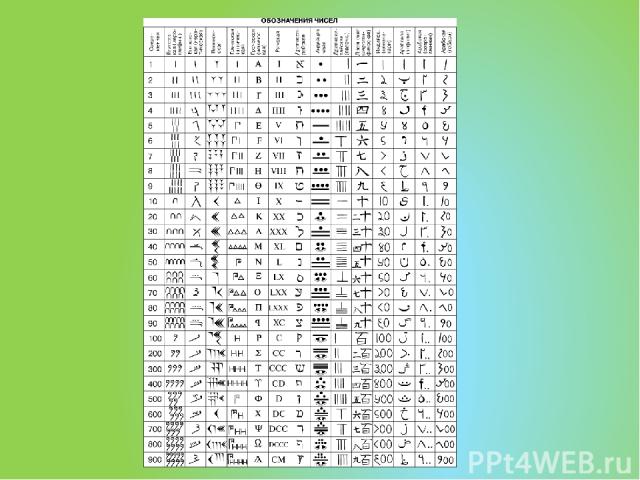
наиболее известные нумерации мира  Древнеегипетская нумерация  Древнегреческая нумерация  Вавилонская нумерация  Нумерация индейцев Майя  Старо-Китайская нумерация  Славянская кириллическая нумерация  Славянская глаголическая нумерация  Латинская нумерация  Современная арабская нумерация и др.

Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, которые называют цифрами.

позиционные непозиционные системы счисления

Непозиционной называют систему счисления, в которой количественное значение цифры не зависит от ее положения в числе. Непозиционные системы счисления

Позиционной называют систему счисления, в которой количественное значение цифры зависит от ее положения в числе. Позиционные системы счисления

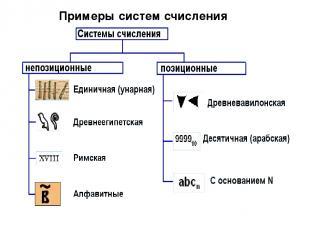
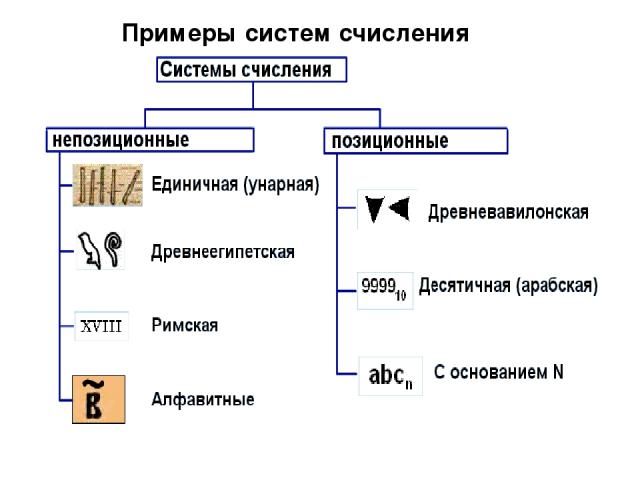
Примеры систем счисления

двоичная, восьмеричная, шестнадцатеричная (информатика) двенадцатеричная (1 фут = 12 дюймов, 1 шиллинг = 12 пенсов) двадцатеричная (1 франк = 20 су) шестидесятеричная (1 минута = 60 секунд, 1 час = 60 минут) Примеры систем счисления

Потребность в записи чисел появилась в очень древние времена, как только люди начали считать. Количество предметов, например овец, изображалось нанесением чёрточек или засечек на какой - либо твёрдой поверхности: камне, глине, дереве (до изобретения бумаги было ещё очень и очень далеко). Каждой овце в такой записи соответствовала одна чёрточка. Археологами найдены такие "записи" при раскопках культурных слоёв, относящихся к периоду палеолита (10 - 11 тысяч лет до н.э.). В этой системе счисления для записи чисел используется только одна цифра. Ее можно изобразить в виде палочки , кружочка , или любой другой фигуры. Числа будут записываться примерно так: 1 2   3     4       5          и т. д. Такая система счисления использовалась, и до сих пор используется в основном народами, не имеющими письменности. Учёные назвали этот способ записи чисел единичной ("палочной") системой счисления. В ней для записи чисел применялся только один вид знаков - "палочка". Каждое число в такой системе счисления обозначалось с помощью строки, составленной из палочек, количество которых и равнялось обозначаемому числу. Неудобства такой системы записи чисел и ограниченность её применения очевидны: чем большее число надо записать, тем длиннее строка из палочек. Да и при записи большого числа легко ошибиться, нанеся лишнее количество палочек или, наоборот, не дописав их. Единичная непозиционная система счисления Унарная – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …)

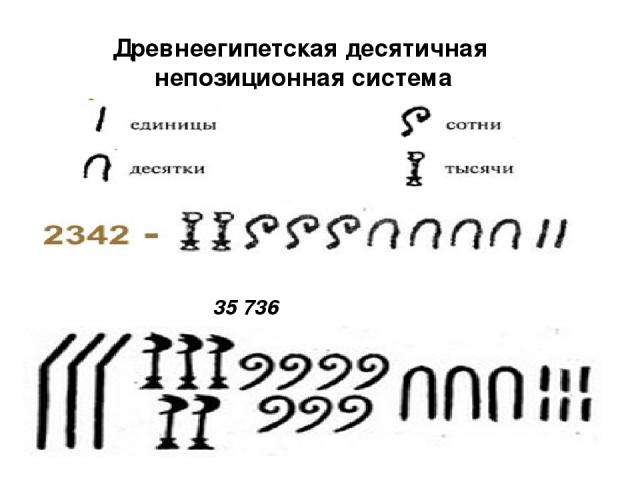
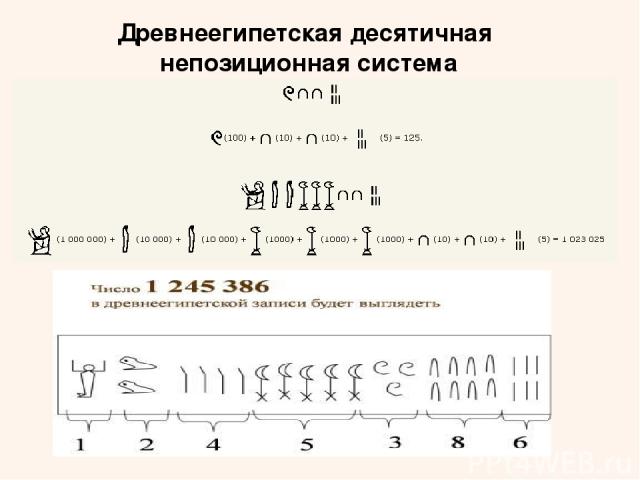
Древнеегипетская десятичная непозиционная система Египтяне придумали эту систему около 5 000 лет тому назад. Это одна из древнейших систем записи чисел, известная человеку. В древнеегипетской системе счисления, которая возникла во второй половине третьего тысячелетия до н.э., использовались специальные цифры для обозначения чисел 1, 10, 102, 103, 104, 105, 106, 107. Числа в египетской системе счисления записывались как комбинации этих цифр, в которых каждая из них повторялась не более девяти раз.

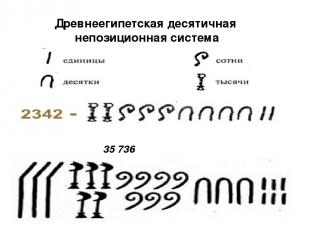
Древнеегипетская десятичная непозиционная система 35 736

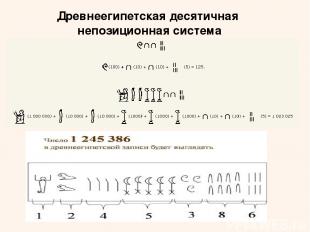
Древнеегипетская десятичная непозиционная система

Вавилонская позиционная шестидесятеричная система Первая позиционная система счисления была придумана еще в древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной, то есть в ней использовалось шестьдесят цифр. Числа составлялись из знаков двух видов: Единицы –прямой клин Десятки – лежачий клин Сотни

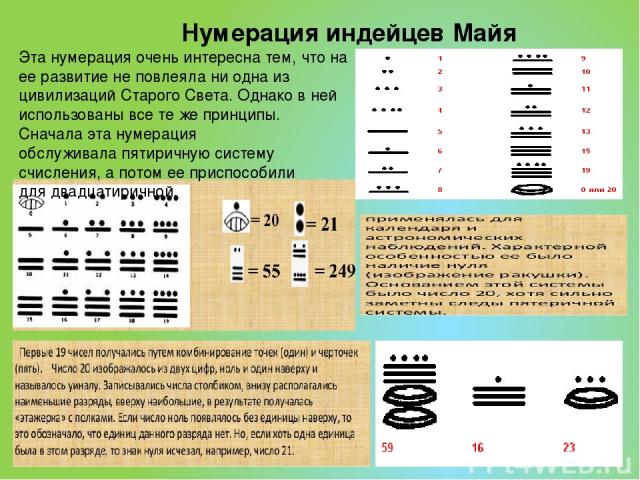
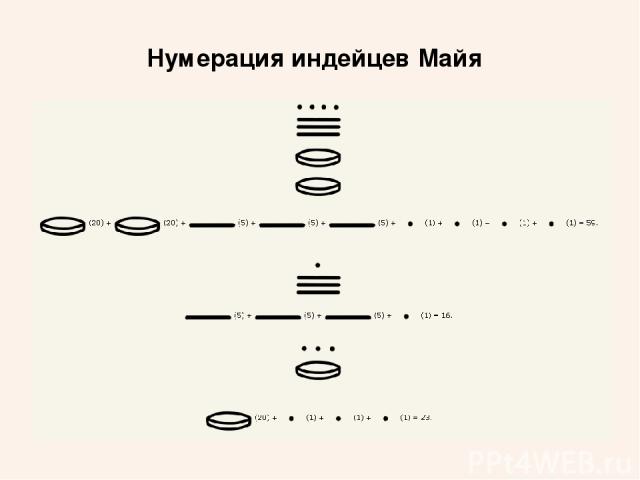
Нумерация индейцев Майя Эта нумерация очень интересна тем, что на ее развитие не повлеяла ни одна из цивилизаций Старого Света. Однако в ней использованы все те же принципы. Сначала эта нумерация обслуживала пятиричную систему счисления, а потом ее приспособили для двадцатиричной.

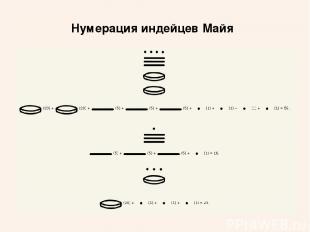
Нумерация индейцев Майя

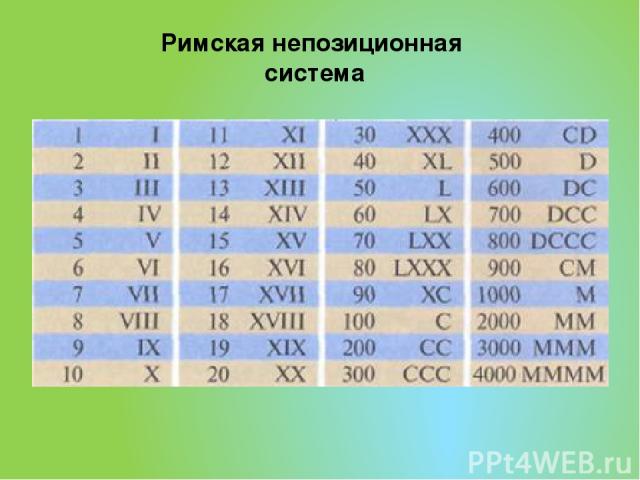
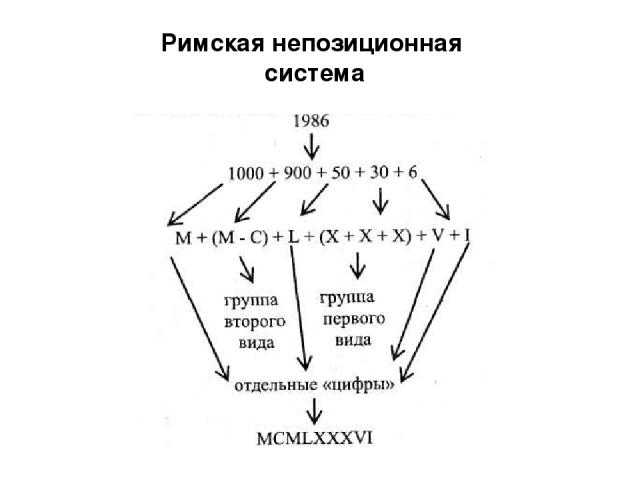
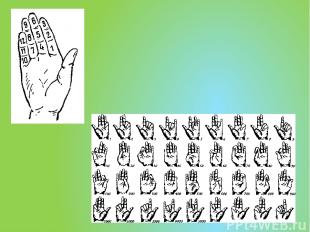
Римская непозиционная система

I – 1 (палец), V – 5 (раскрытая ладонь, 5 пальцев), X – 10 (две ладони), L – 50, C – 100 (Centum), D – 500 (Demimille), M – 1000 (Mille) Римская непозиционная система

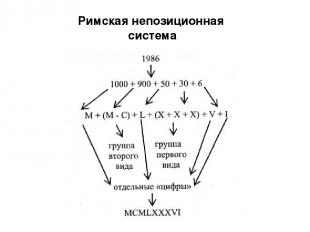
Римская непозиционная система

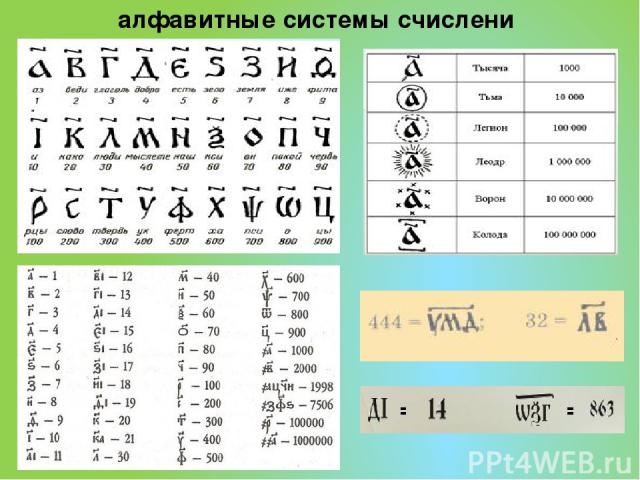
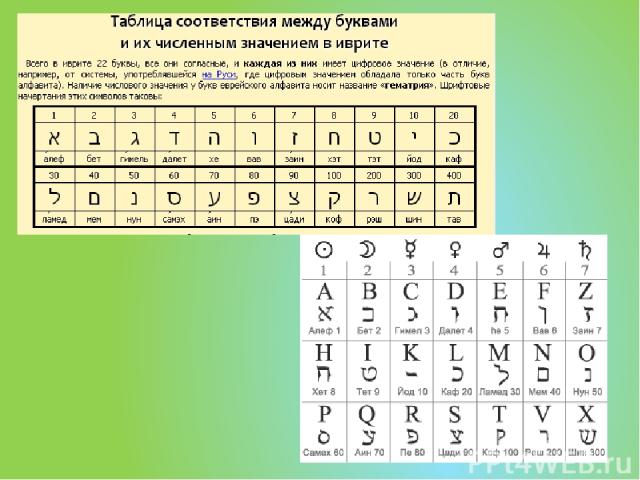
алфавитные системы счислени

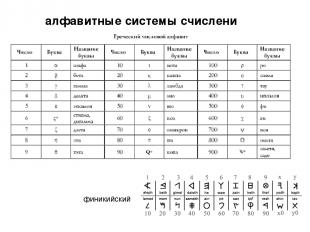
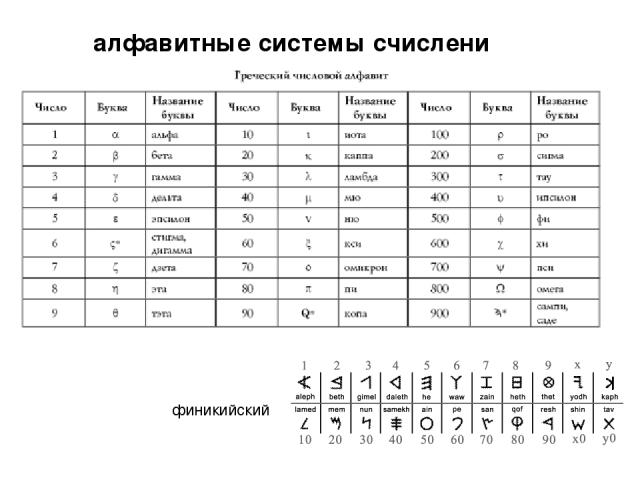
алфавитные системы счислени финикийский 

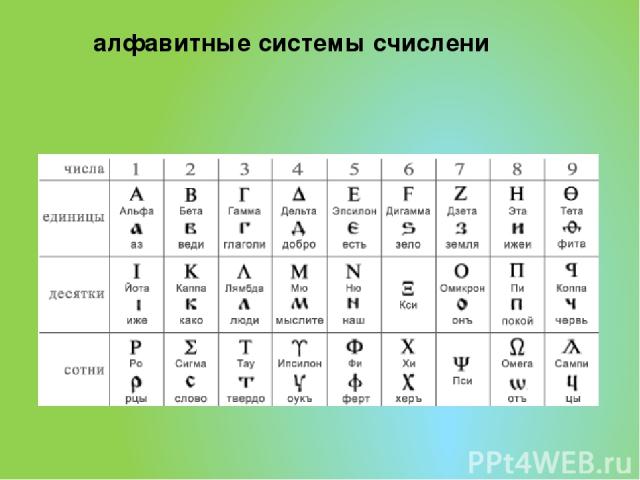
алфавитные системы счислени

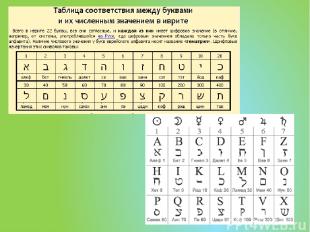
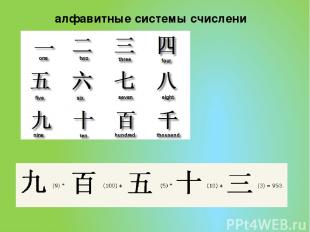
алфавитные системы счислени

Задачи

MDCCLXXXII

MDCCLXXXII = 1000 + 500 + 100 + 100 + 50 + 3*10 + 2 = 1782

 MDCCLXXXII = 1000 + 500 + 100 + 100 + 50 + 3*10 + 2 = 1782 Это год открытия памятника. На гранитном постаменте памятника Петру I в Санкт- Петербурге есть римское число: