Презентация на тему: Преобразование графиков функций на координатной плоскости

Тема урока: Тема урока: Преобразование графиков функций на координатной плоскости.

Красота в единстве теории и практики. Красота в единстве теории и практики.

Рациональные способы построения графиков функций. Рациональные способы построения графиков функций. Развитие пространственного и логического мышления учащихся. Воспитание творческого подхода к решению задач алгебры.

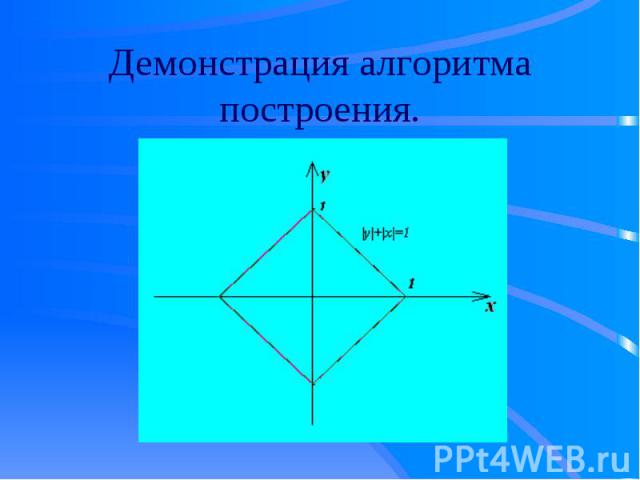
Изобразить в координатной плоскости ХОУ заданные соотношения между переменными х и у, если |x| +|y| = 1. Изобразить в координатной плоскости ХОУ заданные соотношения между переменными х и у, если |x| +|y| = 1.

Первый способ построения графика функции – это построение требуемого графика путем преобразований на координатной плоскости. Первый способ построения графика функции – это построение требуемого графика путем преобразований на координатной плоскости.

у1 = х –прямая – биссектриса 1 и 3 четверти координатной плоскости. у1 = х –прямая – биссектриса 1 и 3 четверти координатной плоскости. у2 = |x| – строим путем отображения графика функции у1 относительно оси (ох) в верхнюю полуплоскость. у3 = -|x| – отображаем график функции у2 относительно оси (ох) в нижнюю полуплоскость. у4 = -|x| + 1 –параллельный перенос графика функции у3 по оси (оу) на 1 вверх. |y| = -|x| + 1 –отбрасываем часть графика у4 в нижней полуплоскости и оставшуюся часть отображаем относительно оси (ох) в нижнюю полуплоскость, тогда получим требуемый график заданной функции |y| + |x| = 1.

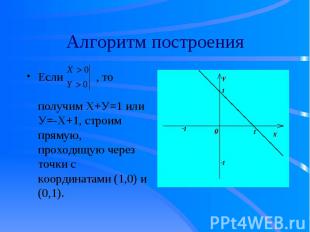
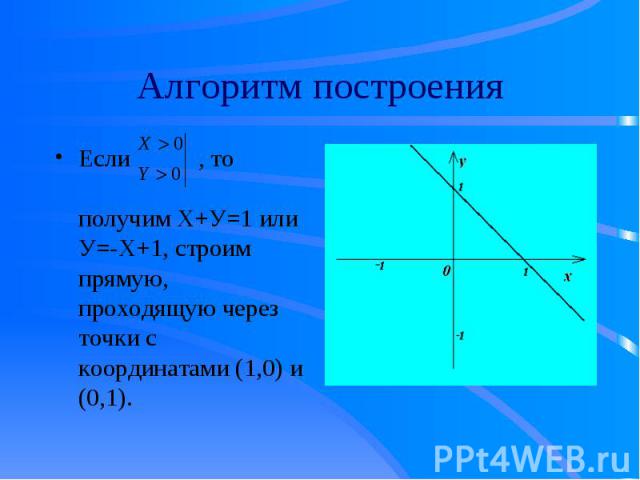
Если , то получим Х+У=1 или У=-Х+1, строим прямую, проходящую через точки с координатами (1,0) и (0,1). Если , то получим Х+У=1 или У=-Х+1, строим прямую, проходящую через точки с координатами (1,0) и (0,1).

В построенном графике – прямой уберем , то на координатной плоскости от прямой останется отрезок с концами на координатных осях В построенном графике – прямой уберем , то на координатной плоскости от прямой останется отрезок с концами на координатных осях

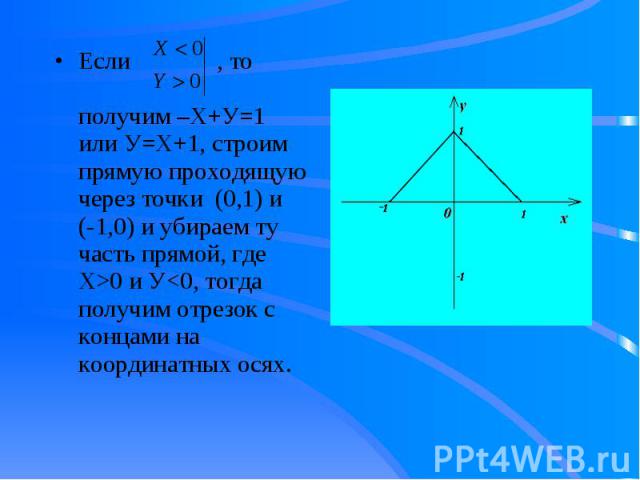
Если , то получим –Х+У=1 или У=Х+1, строим прямую проходящую через точки (0,1) и (-1,0) и убираем ту часть прямой, где Х>0 и У<0, тогда получим отрезок с концами на координатных осях. Если , то получим –Х+У=1 или У=Х+1, строим прямую проходящую через точки (0,1) и (-1,0) и убираем ту часть прямой, где Х>0 и У<0, тогда получим отрезок с концами на координатных осях.

Аналогично построим графики - прямые в третьей и четвертой четвертях координатной плоскости раскрыв модули функции при 1) Х< 0 и У< 0, 2) Х >0 и У <0 соответственно, тогда получим требуемый график функции. Аналогично построим графики - прямые в третьей и четвертой четвертях координатной плоскости раскрыв модули функции при 1) Х< 0 и У< 0, 2) Х >0 и У <0 соответственно, тогда получим требуемый график функции.

А знаете ли вы другие способы построения графика функции? А знаете ли вы другие способы построения графика функции? Об остальных способах поговорим на следующем уроке. До свидания!