Презентация на тему: Синус, косинус, тангенс и котангенс

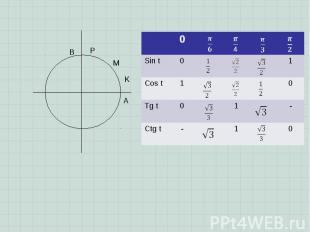
Построение. Построение. ABC – прямоуг. А = – острый Найдем: sin = cos = tg = ctg =

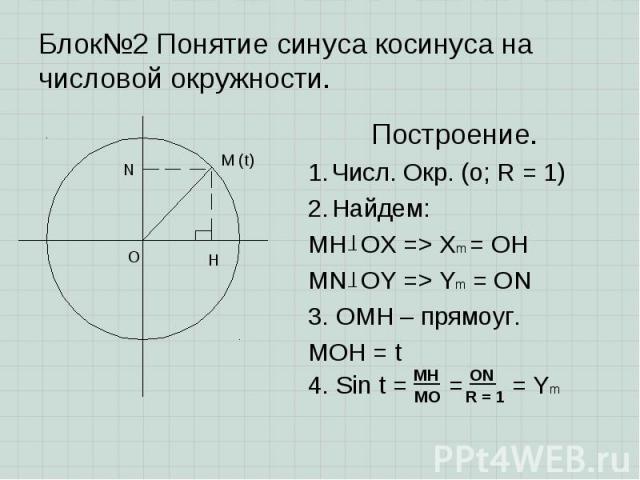
Построение. Построение. Числ. Окр. (о; R = 1) Найдем: MH OX => Xm = OH MN OY => Ym = ON 3. OMH – прямоуг. MOH = t 4. Sin t = = = Ym

Sin t => Ym => OY – ось синусов Sin t => Ym => OY – ось синусов 5. Cos t = = = Xm cos t = Xm => OX – ось косинусов 6. Получили: M(t) => (Xm; Ym) =>

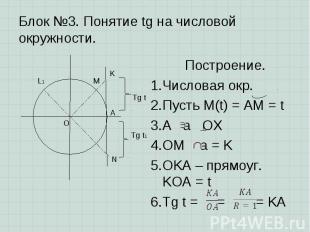
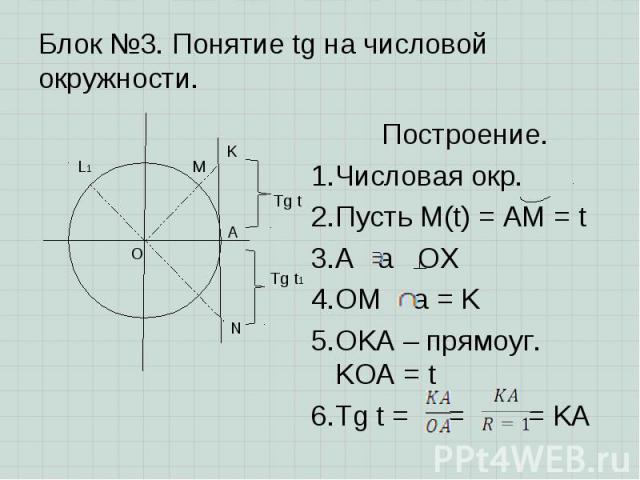
Построение. Построение. Числовая окр. Пусть M(t) = AM = t A a OX OM a = K OKA – прямоуг. KOA = t Tg t = = = KA

7. Tg t = KA => a - ось тангенсов 7. Tg t = KA => a - ось тангенсов Замечание. Пусть L(t1) второй четверти tg t1 = A < 0 Получили: Tg t > 0, если t первой, третей чет. Tg t < 0, если t второй, четвертой чет. 3. Найдем: Tg - не сущ. Tg 0 = tg = 0 Tg - не сущ. Tg t =

Построение: Построение: Числовая окр. Пусть M(t) B b OY OM b = K OBK – прямоуг. OBK = t Ctg t = = = BK

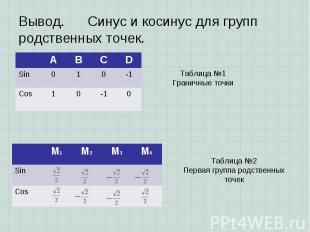
7. Ctg t = BK => b – ось котангенсов 7. Ctg t = BK => b – ось котангенсов Замечание: Ctg t > 0, если t первой, третей четв. Ctg t 0 – не существует Ctg = ctg = 0 Ctg - не существует Таблица №1. Значение tg и ctg граничные точки

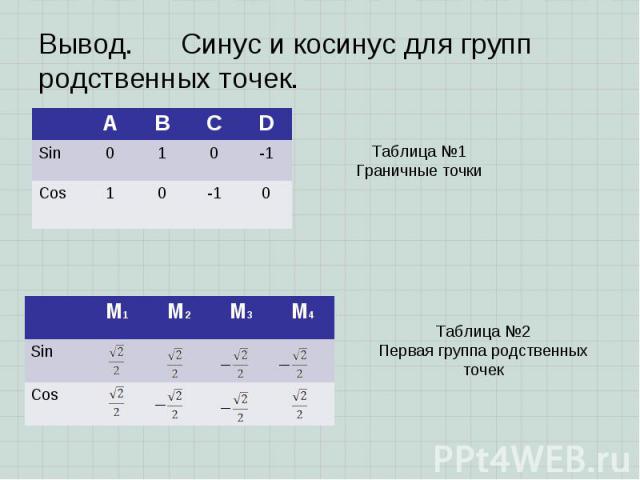
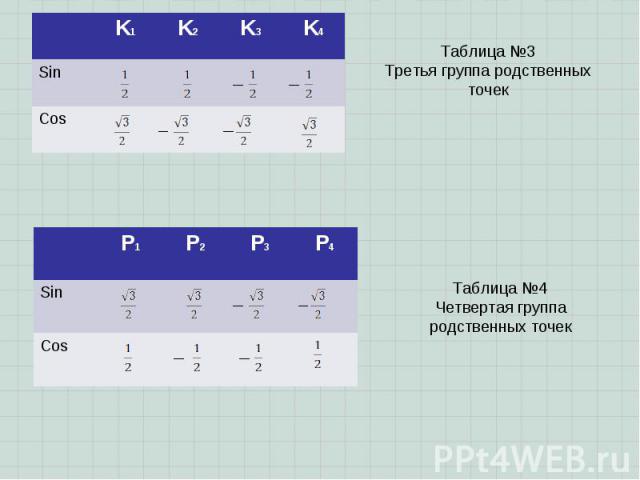
Таблица №2. Первая группа родственных точек. Таблица №2. Первая группа родственных точек.

Формулы: Формулы: sin(-t) = - sin t 2. sin(t+2 k) = sin t cos(-t) = cos t cos(t+2 k) = cos t 3. sin(t+ ) = - sin t 4. tg t = cos(t+ ) = - cos t ctg t = 5. tg (-t) = - tg t 6. tg(t+ ) = tg t ctg (-t) = - ctg t ctg(t+ ) = ctg t 7. tg(t+ k) = tg t ctg(t+ k) = ctg t