Презентация на тему: Методы решения уравнений высших степеней

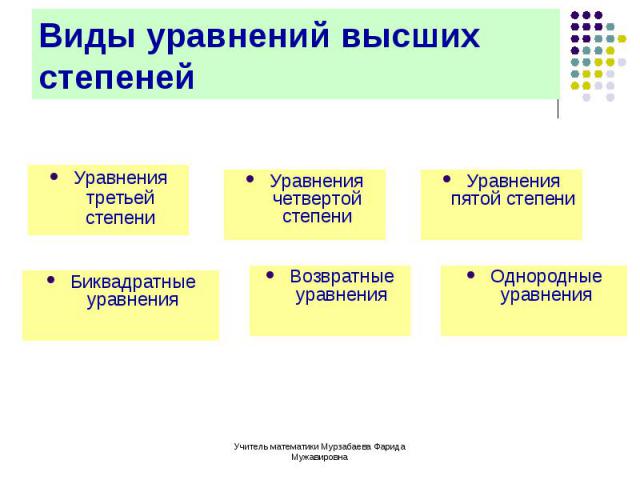
Уравнения третьей степени Уравнения третьей степени

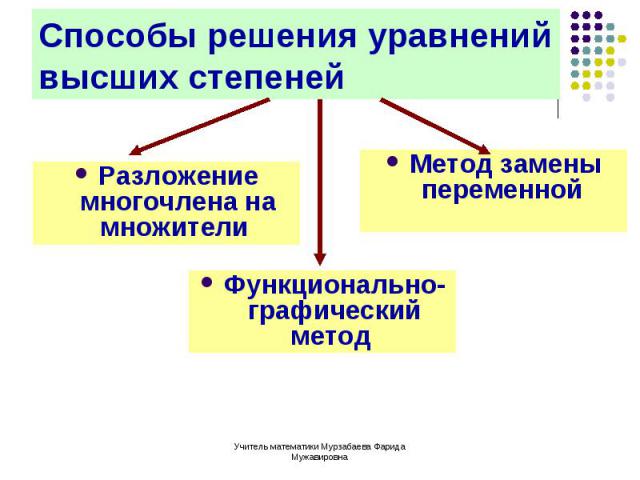
Разложение многочлена на множители Разложение многочлена на множители

Способ группировки Способ группировки

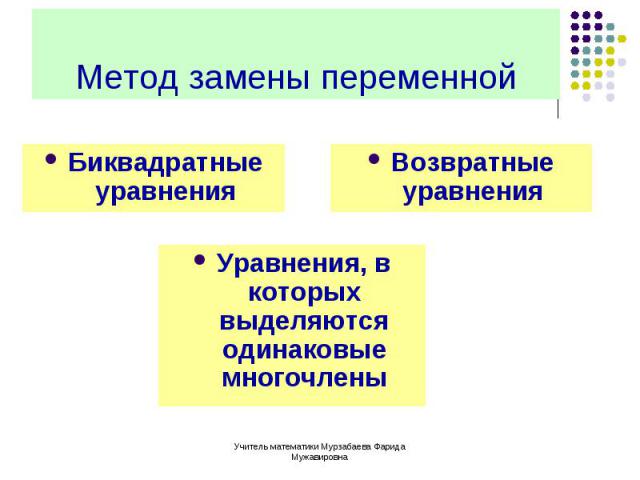
Биквадратные уравнения Биквадратные уравнения

Для уравнений третьей и четвертой степени есть формулы корней (формулы Кордано и Феррари), выведенные итальянскими математиками в 1545 году, но в силу своей громоздкости эти формулы не используют в школьной программе. После того, как были выведены формулы корней для уравнений третьей и четвёртой степени, на протяжении почти 300 лет, учёные-математики пытались вывести формулы для нахождения корней уравнений пятой степени и выше, но труды их оказались безуспешными. Для уравнений третьей и четвертой степени есть формулы корней (формулы Кордано и Феррари), выведенные итальянскими математиками в 1545 году, но в силу своей громоздкости эти формулы не используют в школьной программе. После того, как были выведены формулы корней для уравнений третьей и четвёртой степени, на протяжении почти 300 лет, учёные-математики пытались вывести формулы для нахождения корней уравнений пятой степени и выше, но труды их оказались безуспешными.

В 1826 году норвежский математик Абель доказал, что нельзя вывести формулы для решения уравнений пятой степени и выше. В 1826 году норвежский математик Абель доказал, что нельзя вывести формулы для решения уравнений пятой степени и выше.

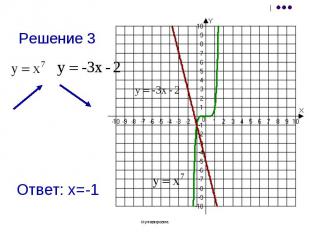
Ответ: уравнение не имеет корней Ответ: уравнение не имеет корней

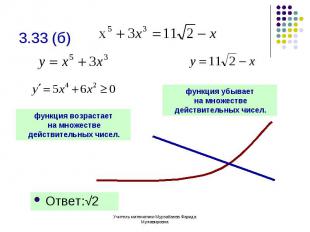
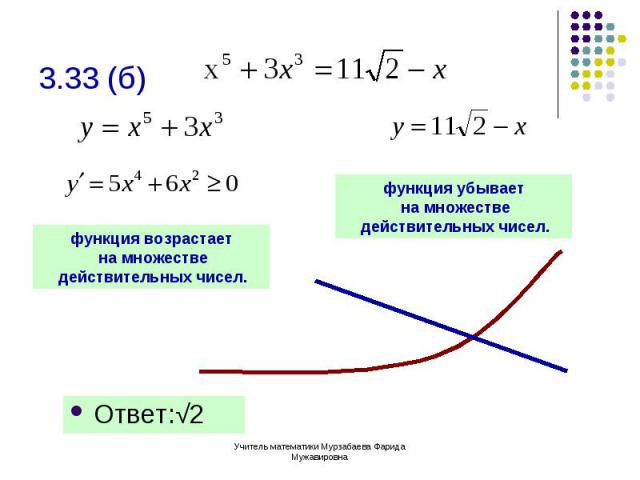
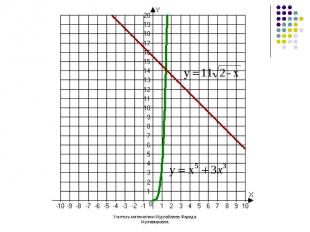
Ответ:√2 Ответ:√2

Ответ: -3; Ответ: -3;

Это возвратное уравнение. Разделим обе части на Это возвратное уравнение. Разделим обе части на

За верное решение любого уравнения - 2 балла За верное решение любого уравнения - 2 балла 2 балла – оценка «3» 4 балла – оценка «4» 6 баллов – оценка «5»