Презентация на тему: Квадратные уравнения 8 класс

Конспект урока алгебры в 8 классе по теме: «Квадратные уравнения». Автор: Обухова Елена Александровна, учитель математики МОУ СОШ № 12 г. Сочи, Краснодарского края. 2009 г. 900igr.net

Тип урока: обобщение. Цели урока: Образовательные: а). Обобщение и систематизация знаний учащихся по теме «Алгебраические дроби». б). Закрепление навыков решения тестовых заданий по данной теме. Развивающие: а). Формирование и развитие умения мыслить и анализировать. б). Развитие памяти. Воспитывающие: а). Воспитание умения работать самостоятельно. б). Воспитание умения выдерживать регламент времени, отведенного на решение каждого задания. в). Привитие интереса к предмету.

Повторение основных понятий. Новые термины математического языка. Квадратное уравнение – уравнение вида ах2+вх+с=0, где а,в,с – любые числа, причем а≠0. Приведенное уравнение – если его старший коэффициент (а) равен 1. Неполное уравнение – если хотя бы один из коэффициентов (в,с) равен 0. Такое уравнение имеет виды: ах2=0, ах2+вх=0, ах2+с=0.

4. Корень уравнения – значение переменной, при котором квадратный трехчлен обращается в нуль. Количество корней уравнения зависит от его ДИСКРИМИНАНТА. 5. Биквадратное уравнение – уравнение вида ах4+вх2+с=0, где а,в,с – любые числа, причем а≠0. 6. Иррациональное уравнение – переменная содержится под знаком радикала.

Мы вывели формулы для решения уравнений. ах2+вх+с=0, х1,2= где Д=в2-4ас. 2. ах2+2кх+с=0, х1,2= где Д=к2-ас. 3. ах2+вх+с=а(х-х1)(х-х2) – разложение квадратного трехчлена на множители.

Основные теоремы: О связи корней квадратного уравнения с его дискриминантом: если Д0, то уравнение имеет два различных корня.

Основные теоремы: 2. Теорема Виета (о связи корней с его коэффициентами) для уравнения ах2+вх+с=0 – х1+х2=-в/а, х1х2=с/а. для приведенного уравнения х2+рх+q=0 х1+х2=-р, х1х2=q.

Вспомним как решать: 2х2-7х=0 Х2-16=0 3х2+10=0 5х2=0 Подсказки: х(2х-7)=0, х1=?, х2=? Х2=16, х1=?, х2=? 3х2=-10, Ответ: ? Х2=0:5, х2=?, х=?

Вспомним как решать: 5. 2х2+4х+7=0 6. х2-6х+9=0 7. х2-2х-3=0 Подсказки: 5. Д=-40, Ответ: ? 6. Д=0, х=? 7. Д=16, х1=?, х2=? или х1+х2=2, х1х2=-3, х1=?, х2=?

Вспомним как решать: 8. х4+х2-20=0 (используется метод замены переменной) 9. √5х-16=х-2 (используется метод возведения обеих частей в квадрат; обязательно сделать проверку корней) Подсказки: 8. Пусть х2=к,получим к2+к-20=0, к1=4, к2=-5 Значит,х2=4 или х2=-5 х1=?, х2=?, х3=?, х4=? Ответ: ? 9. 5х-16=(х-2)2 х2-9х+20=0 х1=?, х2=? Проверка!!! Ответ: ?

Самостоятельная работа. Выполните тест:

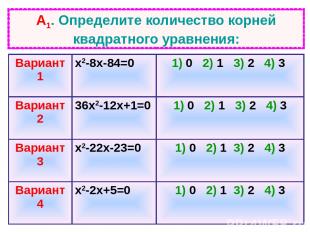
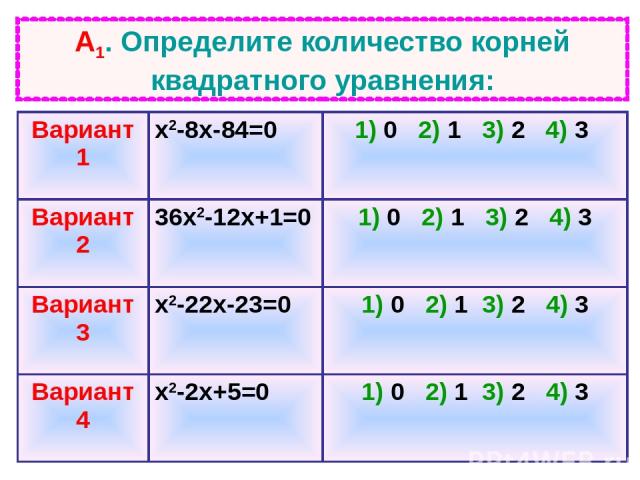
А1. Определите количество корней квадратного уравнения: Вариант 1 х2-8х-84=0 1) 0 2) 1 3) 2 4) 3 Вариант 2 36х2-12х+1=0 1) 0 2) 1 3) 2 4) 3 Вариант 3 х2-22х-23=0 1) 0 2) 1 3) 2 4) 3 Вариант 4 х2-2х+5=0 1) 0 2) 1 3) 2 4) 3

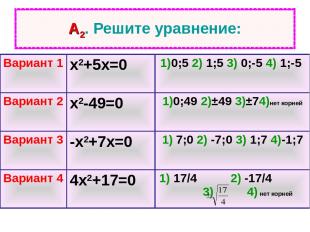
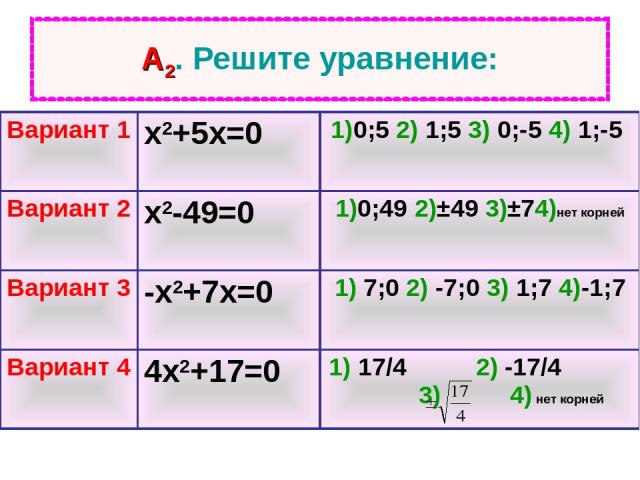
А2. Решите уравнение: Вариант 1 х2+5х=0 1)0;5 2) 1;5 3) 0;-5 4) 1;-5 Вариант 2 х2-49=0 1)0;49 2)±49 3)±74)нет корней Вариант 3 -х2+7х=0 1) 7;0 2) -7;0 3) 1;7 4)-1;7 Вариант 4 4х2+17=0 1) 17/4 2) -17/4 3) 4) нет корней

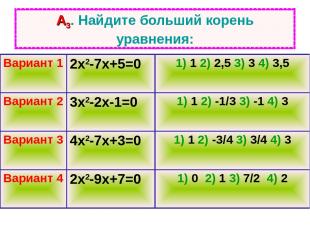
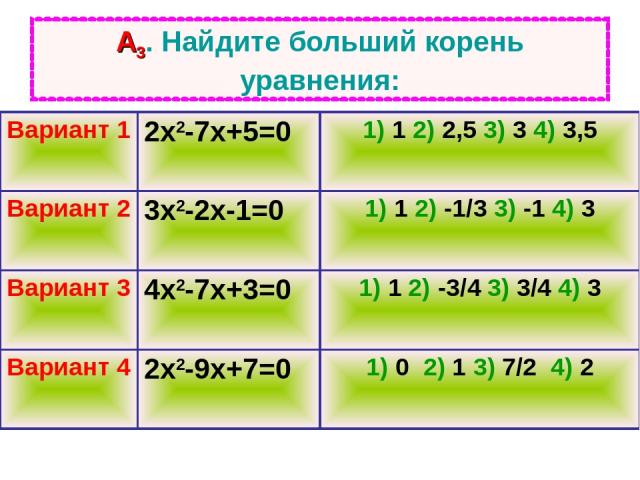
А3. Найдите больший корень уравнения: Вариант 1 2х2-7х+5=0 1) 1 2) 2,5 3) 3 4) 3,5 Вариант 2 3х2-2х-1=0 1) 1 2) -1/3 3) -1 4) 3 Вариант 3 4х2-7х+3=0 1) 1 2) -3/4 3) 3/4 4) 3 Вариант 4 2х2-9х+7=0 1) 0 2) 1 3) 7/2 4) 2

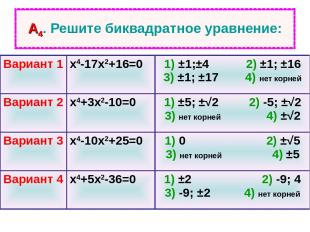
А4. Решите биквадратное уравнение: Вариант 1 х4-17х2+16=0 1) ±1;±4 2) ±1; ±16 3) ±1; ±17 4) нет корней Вариант 2 х4+3х2-10=0 1) ±5; ±√2 2) -5; ±√2 3) нет корней 4) ±√2 Вариант 3 х4-10х2+25=0 1) 0 2) ±√5 3) нет корней 4) ±5 Вариант 4 х4+5х2-36=0 1) ±2 2) -9; 4 3) -9; ±2 4) нет корней

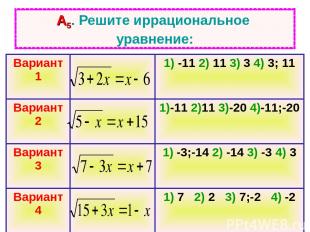
А5. Решите иррациональное уравнение: Вариант 1 1) -11 2) 11 3) 3 4) 3; 11 Вариант 2 1)-11 2)11 3)-20 4)-11;-20 Вариант 3 1) -3;-14 2) -14 3) -3 4) 3 Вариант 4 1) 7 2) 2 3) 7;-2 4) -2

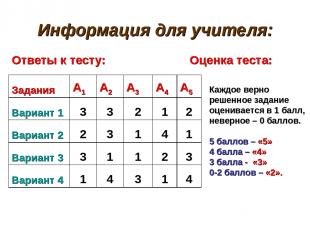
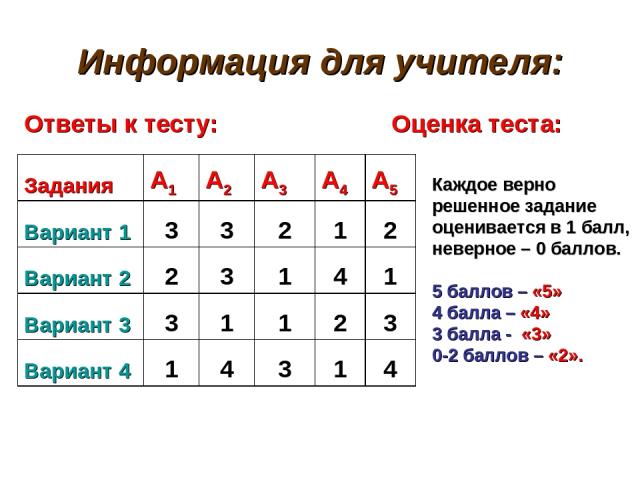
Информация для учителя: Ответы к тесту: Оценка теста: Каждое верно решенное задание оценивается в 1 балл, неверное – 0 баллов. 5 баллов – «5» 4 балла – «4» 3 балла - «3» 0-2 баллов – «2». Задания А1 А2 А3 А4 А5 Вариант 1 3 3 2 1 2 Вариант 2 2 3 1 4 1 Вариант 3 3 1 1 2 3 Вариант 4 1 4 3 1 4

Используемая литература: «Алгебра 8 класс», часть 1, учебник, под редакцией А.Г. Мордковича, Мнемозина, 2007 г. «Алгебра 8 класс», часть 2, задачник, под редакцией А.Г. Мордковича, Мнемозина, 2007 г. «Тематический сборник тестовых заданий по алгебре для подготовки к государственной (итоговой) аттестации в новой форме», базовый уровень, под редакцией Е.А. Семенко, Просвещение-Юг, Краснодар, 2008 г. «Экзаменационные тестовые задания», Федеральная служба по надзору в сфере образования и науки РФ, 2008 г. «Краевые диагностические работы по алгебре в 9 классе», Департамент образования и науки Краснодарского края, ККИДППО, 2008 г.