Презентация на тему: Квадратные неравенства

Далее 900igr.net

Памятка Квадратные неравенства Тест О продукте Выход

Понятие квадратного уравнения Понятие неравенства Свойства неравенств К содержанию

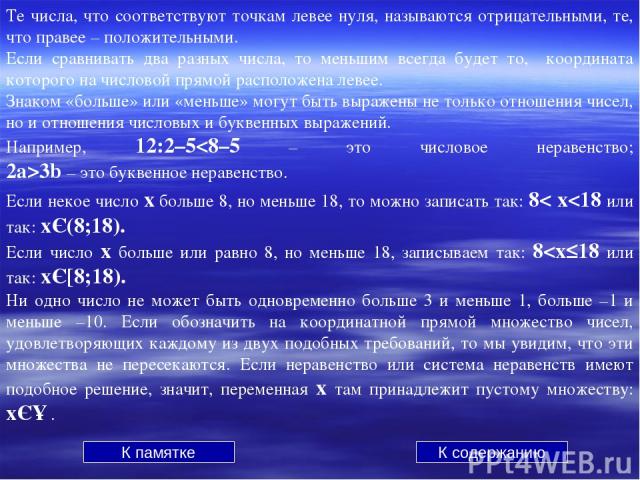
Вспомним в общих чертах, что означает «больше» и «меньше» в алгебре. В обычной жизни мы точно знаем, что 3 меньше 4, а 8 больше 2. Никто не сомневается, что килограмм апельсинов больше, чем полкило. Однако, начиная оперировать цифрами, мы сталкиваемся с интересной вещью: половина неожиданно может оказаться больше целого! Это происходит в том случае, если перед обеими цифрами, 1 и 0,5, стоит знак «минус». То есть: –1 < –0,5  Чтобы легче было понять, какое из двух чисел, независимо от знака, больше, а какое меньше, люди придумали координатную прямую -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 Далее

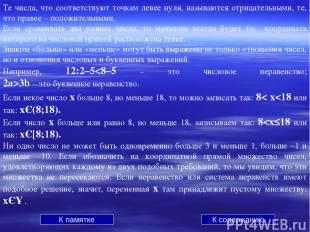
Если некое число х больше 8, но меньше 18, то можно записать так: 8< х

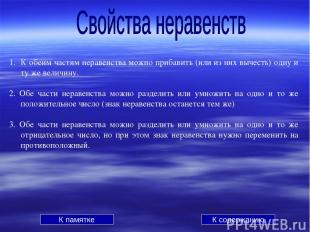
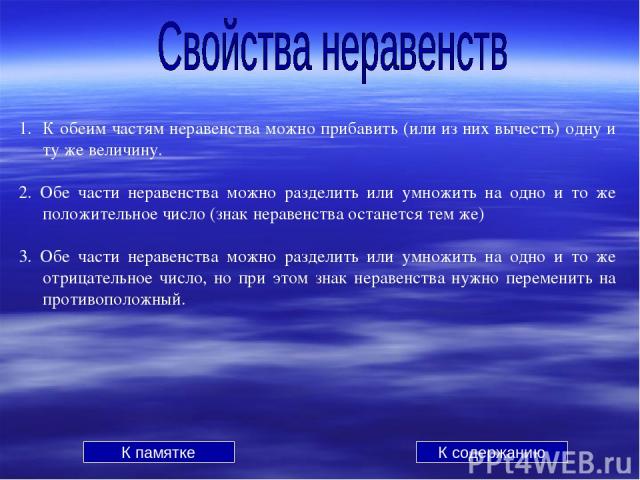
К обеим частям неравенства можно прибавить (или из них вычесть) одну и ту же величину. 2. Обе части неравенства можно разделить или умножить на одно и то же положительное число (знак неравенства останется тем же) 3. Обе части неравенства можно разделить или умножить на одно и то же отрицательное число, но при этом знак неравенства нужно переменить на противоположный. К памятке К содержанию

Квадратным уравнением относительно X называется уравнение вида ах2+bx+c=0 , а≠0. При этом а называют старшим коэффициентом, а с- свободным членом. Квадратное уравнение может иметь один, два, или не иметь вещественных корней. В случае, когда квадратное уравнение имеет один корень иногда говорят, что оно имеет два совпадающих корня. Наличие корней определяется с помощью дискриминанта квадратного уравнения D=b2+ 4ас. Если, D>0 то уравнение имеет два различных корня, если D=0, то уравнение имеет один корень, если D

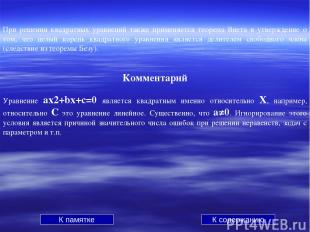
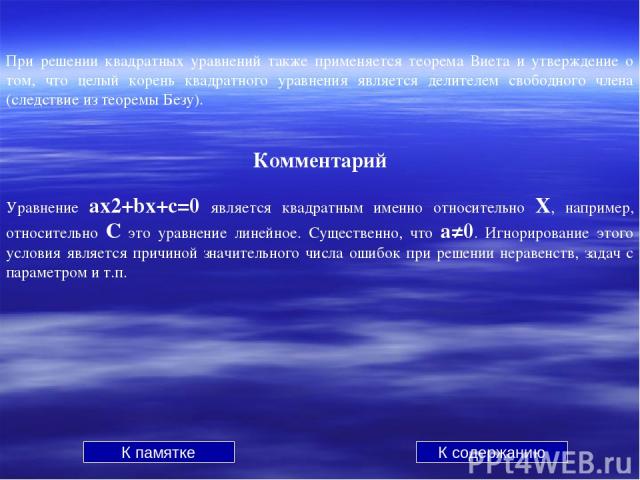
При решении квадратных уравнений также применяется теорема Виета и утверждение о том, что целый корень квадратного уравнения является делителем свободного члена (следствие из теоремы Безу). Комментарий Уравнение ах2+bx+c=0 является квадратным именно относительно Х, например, относительно С это уравнение линейное. Существенно, что а≠0. Игнорирование этого условия является причиной значительного числа ошибок при решении неравенств, задач с параметром и т.п. К памятке К содержанию

Понятие квадратных неравенств Решение квадратных неравенств К содержанию

Пусть f(x)=ax2+bx+c, где a,b,c- заданные числа, причем a≠0, x- неизвестное. Тогда неравенства вида f(x)>0, f(x)0 или ax2+bx+c

Если D=b2-4ac0, при a>0 являются все действительные числа, а неравенство ax2+bx+c0 не имеет решений; Если D=0, то решениями неравенства ax2+bx+c>0, являются все действительные значения x, кроме , а неравенство ax2+bx+c0, то решениями неравенства ax2+bx+c>0 при a>0 являются все числа x такие, что xx2, где x1 и x2  - корни квадратного уравнения ax2+bx+c=0, т. е все значения x, лежащие вне отрезка [x1, x2].  Решениями неравенства ax2+bx+c

1) Рассмотрим квадратичную функцию f(x) = x2 – 5 x - 50 и найдем такие значения x, для которых f(x) < 0. 2) Графиком рассматриваемой функции является парабола, ветви которой направлены вверх, так как a = 1, 1 > 0. 3) Найдем нули функции (то есть абсциссы точек пересечения параболы с осью Ox), для этого решим квадратное уравнение x2 – 5 x – 50 = 0. x2 – 5 x – 50 = 0, a = 1, b = -5, c = -50. D = b2 – 4ac; D = (-5)2 –4*1*(-50) = 25 + 200 = 225 = 152, 225 > 0, значит уравнение имеет два действительных корня. x1 = (-(-5) – 15) : 2 = -5; x2 = (-(-5) + 15) : 2 = 10. Нули функции: x = -5 и x = 10. Далее Метод рассмотрения квадратичной функции

4) Изобразим схематично параболу f(x) = x2 – 5x –50 в координатной плоскости Oxy. 5) Из рисунка видим, что f(x) < 0, при –5 < x < 10 (то есть берем в рассмотрение ту часть параболы, которая лежит ниже оси Ox). Замечание: ответ записываем в виде числового промежутка. Ответ: (-5; 10). К другому методу К содержанию

Метод интервалов Рассмотрим функцию f(x) = x2 – 5x – 50 и найдем такие значения х для которых f(x) < 0. D(f) = R (то есть множество всех действительных чисел). 2) Разложим квадратный трехчлен х2 – 5х - 50 на множители (то есть представим его в виде произведения а(х – х1)(х – х2), где х1 и х 2 – корни квадратного трехчлена). 3) Для нахождения корней квадратного трехчлена решим уравнение х2 – 5х – 50 = 0. (Его мы уже решали, поэтому воспользуемся готовым результатом). Так как х1 = -5, х2 = 10, то получаем следующее разложение квадратного трехчлена на множители х2 – 5х - 50 = (х – (-5))(х – 10) = (х + 5)(х –10). Далее

4) Теперь разобьем D(f) - область определения функции f(x) = x2 – 5x – 50 её нулями, то есть числами –5 и 10, на интервалы, в каждом из которых функция непрерывна, не обращается в ноль и поэтому сохраняет постоянный «знак». 5) Расставляем «знаки» в интервалах: выбираем любое число из соответствующего интервала и определяем «знак» функции (например, 0 принадлежит интервалу (-5; 10) и f(0) = 02 – 5*0 – 50 = -50; то есть f(0) < 0, значит значение функции в любой точке этого интервала отрицательно, ставим «знак» минус…). 6) Выбираем промежутки, в которых f(x) < 0: это выполняется для всех –5 < х < 10. Ответ: (-5; 10). К другому методу К содержанию

Рассмотрим решение квадратных неравенств на конкретном примере. Решим неравенство x2-5x-50

Данный тест поможет правильно оценить Ваши знания. При выполнении задания Вам необходимо выбрать правильный вариант ответа. За каждый верный ответ зачисляется 10 баллов. Максимальное количество баллов 50. Для начала выполнения теста нажмите кнопку далее. Желаю успеха! Далее К содержанию

1. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) . x2–6x–70≥0 Да. Нет.

2. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) . 3–х2≤х Да. Нет.

2. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) . 3–х2≤х Да. Нет.

–х2+6х–5

–х2+6х–5

–х2+6х–5

4. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) . х2-3х+2≤0 Да. Нет.

4. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) . х2-3х+2≤0 Да. Нет.

4. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) . х2-3х+2≤0 Да. Нет.

4. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) . х2-3х+2≤0 Да. Нет.

5. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) . 3х2-5х-2>0 Да. Нет.

5. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) . 3х2-5х-2>0 Да. Нет.

5. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) . 3х2-5х-2>0 Да. Нет.

5. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) . 3х2-5х-2>0 Да. Нет.

5. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно) . 3х2-5х-2>0 Да. Нет.

К содержанию

К содержанию

К содержанию

К содержанию

К содержанию

К содержанию

Выход