Презентация на тему: Информационные модели. Графы

Информационные модели. Графы.

Впервые основы теории графов появились в работах Леонарда Эйлера (1707-1783; швейцарский, немецкий и российский математик) , в которых он описывал решение головоломок и математических развлекательных задач. Теория графов началась с решения Эйлером задачи о семи мостах Кёнигсберга.

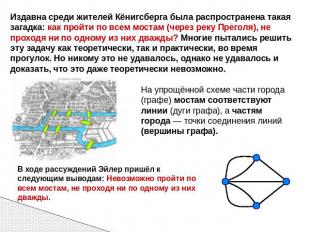
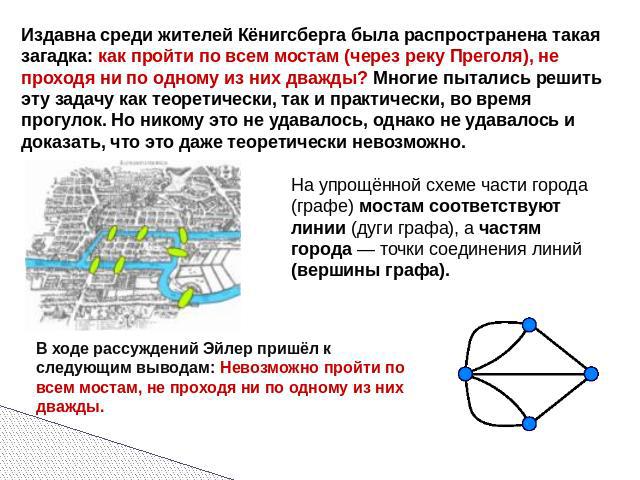
Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам (через реку Преголя), не проходя ни по одному из них дважды? Многие пытались решить эту задачу как теоретически, так и практически, во время прогулок. Но никому это не удавалось, однако не удавалось и доказать, что это даже теоретически невозможно. На упрощённой схеме части города (графе) мостам соответствуют линии (дуги графа), а частям города — точки соединения линий (вершины графа). В ходе рассуждений Эйлер пришёл к следующим выводам: Невозможно пройти по всем мостам, не проходя ни по одному из них дважды.

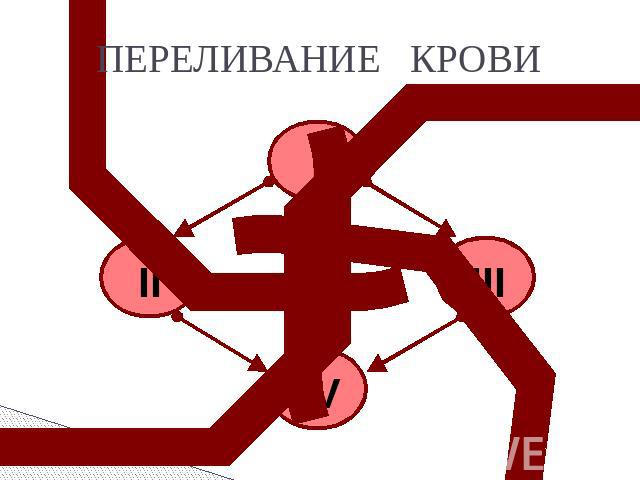
Задача. Существуют 4 группы крови. При переливании крови от одного человека к другому не все группы совместимы. Но известно, что одинаковые группы можно переливать от человека к человеку, т.е. 1 – 1, 2 – 2 и т.д. А также 1 группу можно переливать всем остальным группам, 2 и 3 группу только 4 группе.

ПЕРЕЛИВАНИЕ КРОВИ

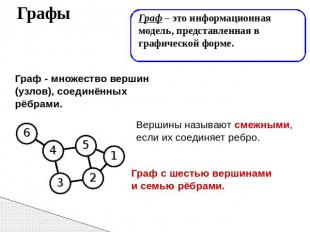
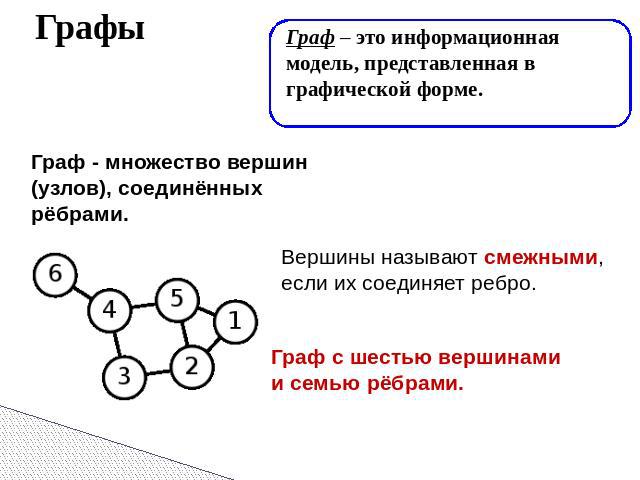
Графы Граф – это информационная модель, представленная в графической форме. Граф - множество вершин (узлов), соединённых рёбрами. Вершины называют смежными, если их соединяет ребро. Граф с шестью вершинами и семью рёбрами.

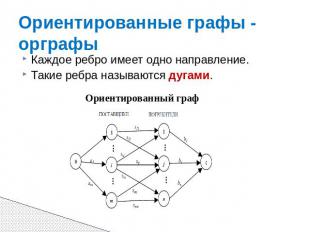
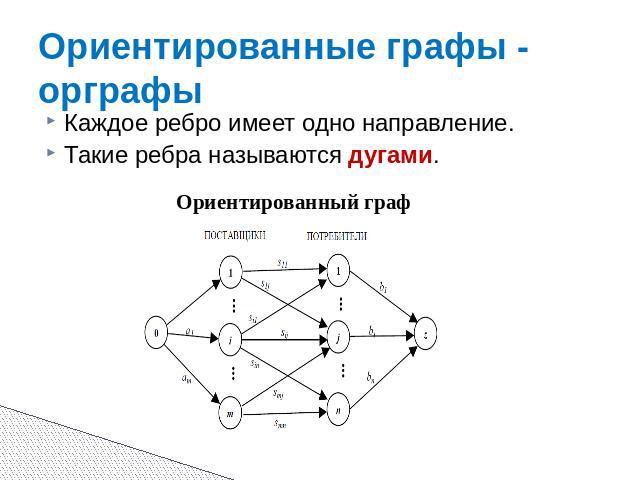
Ориентированные графы - орграфы Каждое ребро имеет одно направление. Такие ребра называются дугами.

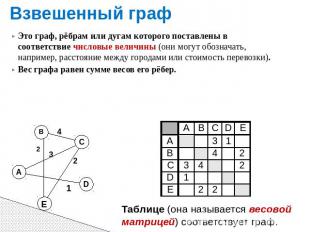
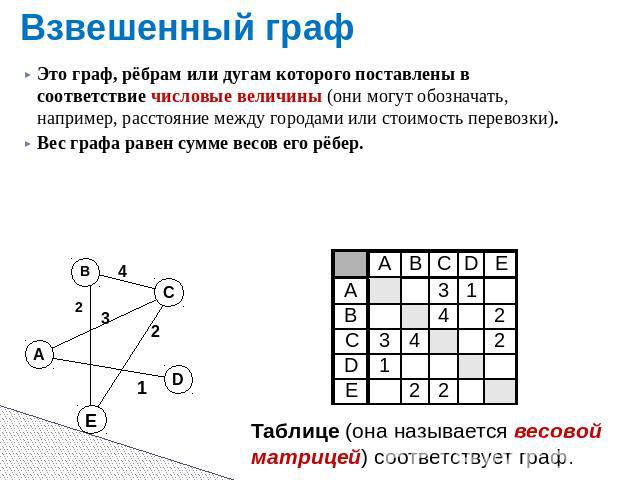
Взвешенный граф Это граф, рёбрам или дугам которого поставлены в соответствие числовые величины (они могут обозначать, например, расстояние между городами или стоимость перевозки). Вес графа равен сумме весов его рёбер.

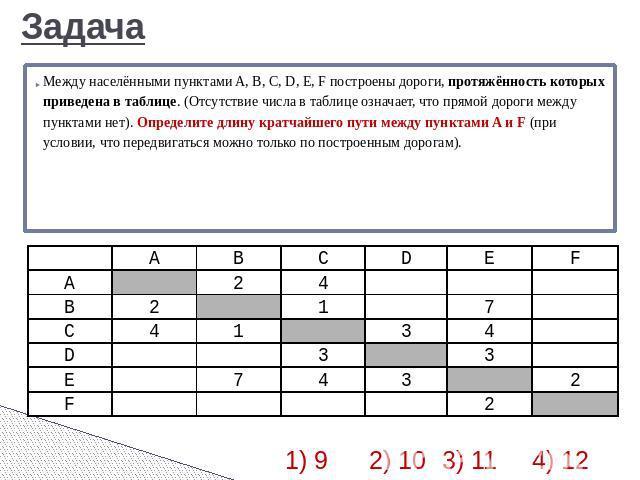
Задача Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет). Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).

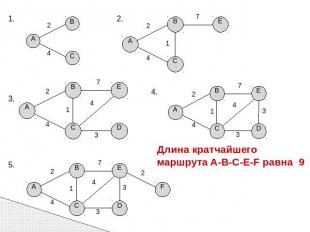
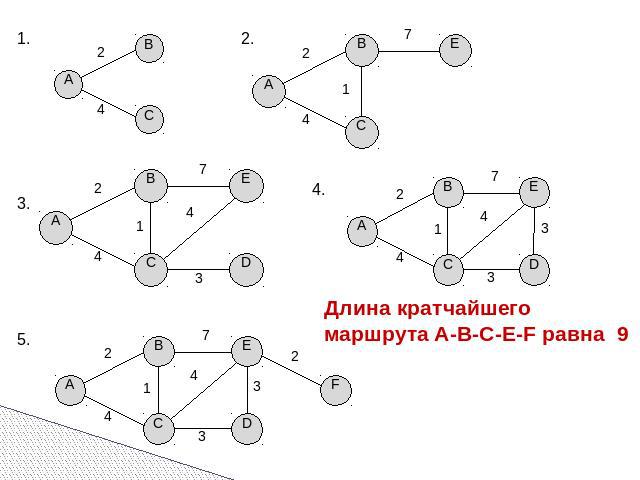
Длина кратчайшего маршрута A-B-C-E-F равна 9

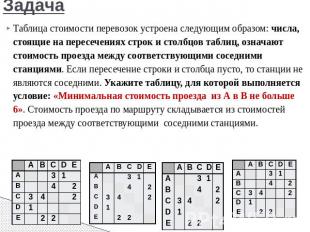
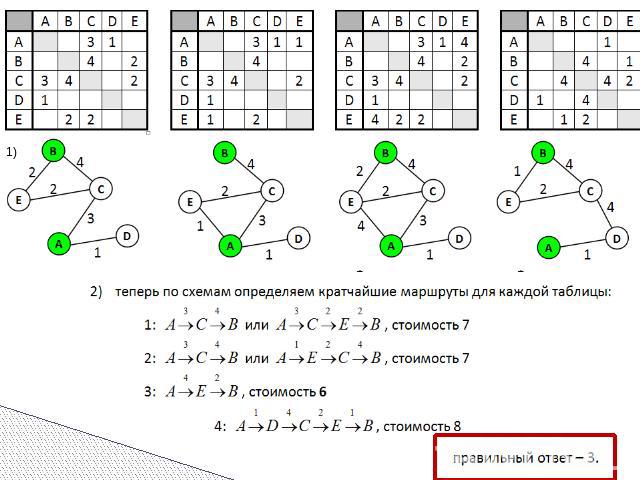
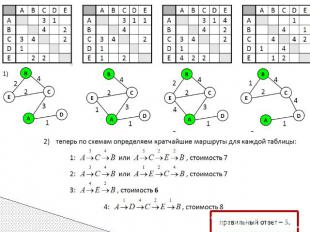
Задача Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость проезда между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними. Укажите таблицу, для которой выполняется условие: «Минимальная стоимость проезда из А в B не больше 6». Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями.

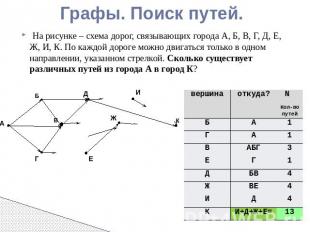
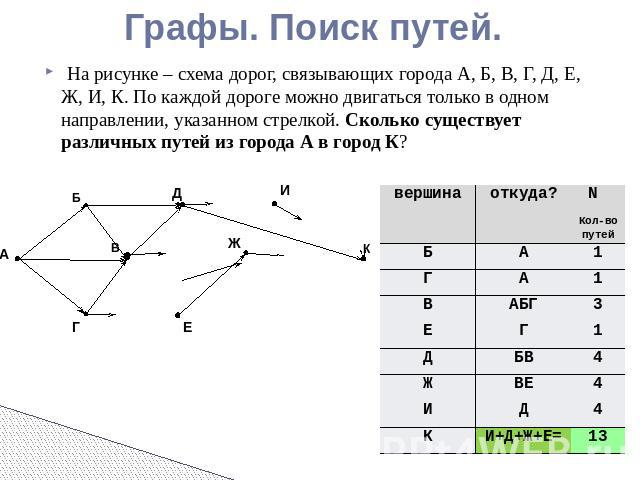
Графы. Поиск путей. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?