Презентация на тему: Баллистическое движение

Баллистическое движение

Баллистика-(греч.- бросать)

-выяснить, что является траекторией движения снаряда;-найти время подъема, высоту подъема;-определить дальность полета, модуль вектора скорости в любой момент времени;

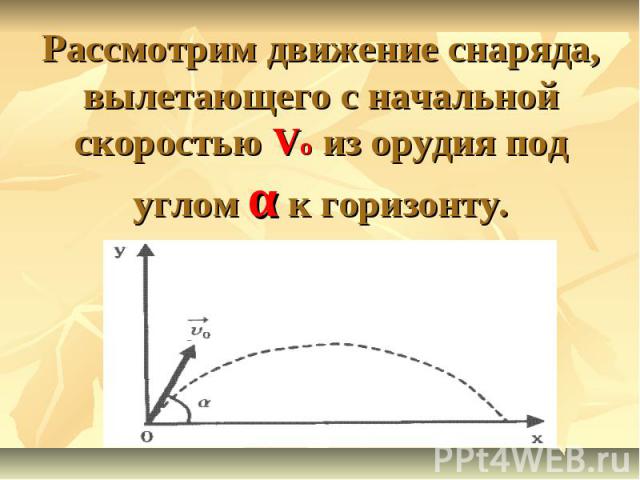
Рассмотрим движение снаряда, вылетающего с начальной скоростью Vo из орудия под углом α к горизонту.

Выберем систему отсчета (СО)

Тело принимает участие одновременно в двух движениях: вдоль оси OX движется равномерно;вдоль оси OY движение равноускоренное.

Предложите свою модель этого движения?

Докажем:x=x0+V0xty=y0+V0yt+gyt²/2ПАРАБОЛА

Запишите уравнения движения для координаты X тела в любой момент времени и для проекции его скорости на ось OXX=VxtX=V0cosα·tVx=constVx=V0cosα

Запишем уравнения движения для координаты Y тела в любой момент времени и для проекции его скорости на ось OYY=Y0+V0y·t+gy·t²/2Vy=V0y+gytY0=0gy= - gV0y=V0sinαY=V0sinα·t-gt²/2Vy=V0sinα-gt

Решим систему уравнений:X=V0cosα·tY=V0sinα·t-gt²/2Y=Y(x)-?t=Y=V0sinα· -g( )²/2

Что же является траекторией движения Y(x)?Обозначим:a=sinα/cosαb=g/2(1/V0cosα)

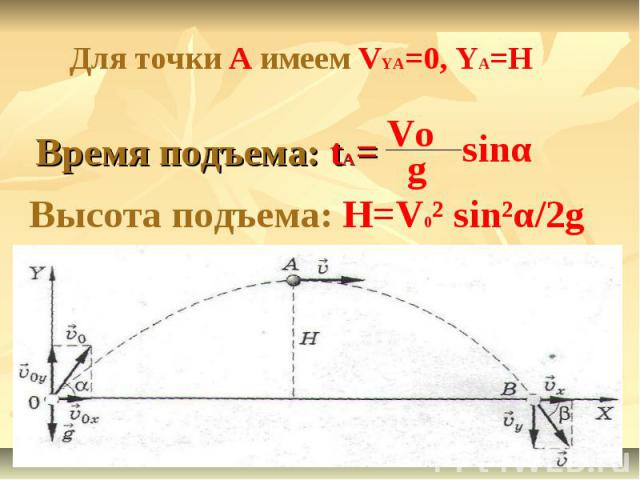
Для точки А имеем VYA=0, YA=HВремя подъема: tA=Высота подъема: H=V0² sin²α
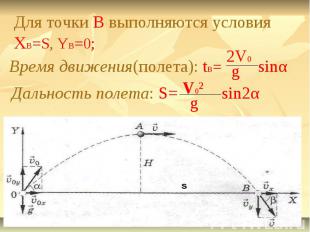
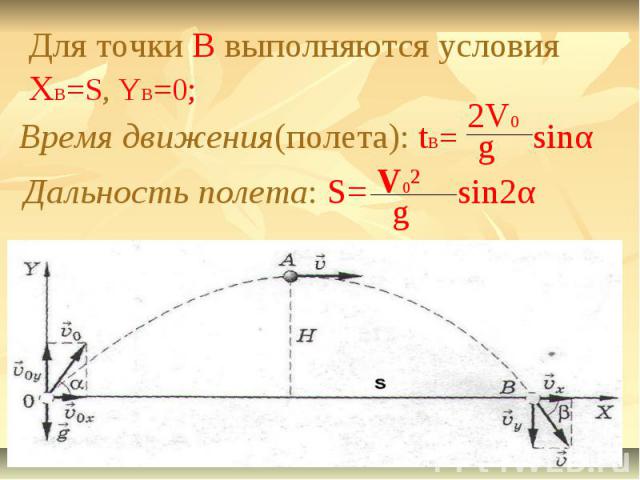
Для точки B выполняются условия XB=S, YB=0;Время движения(полета): tB=Дальность полета: S=
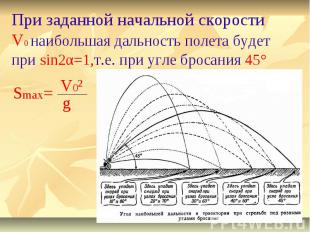
При заданной начальной скорости V0 наибольшая дальность полета будет при sin2α=1,т.е. при угле бросания 45°

Определим модуль и направление вектора скорости:

модуль вектора скорости в любой момент времени:Направление вектора скорости в любой момент времени найдем из формулы:


ИТОГИ УРОКА: