Презентация на тему: Замечательные кривые вокруг нас

Замечательные кривые геометрии вокруг нас Выполнила учитель математики МБОУ «Путиловская СОШ» Семенова Елена Владимировна

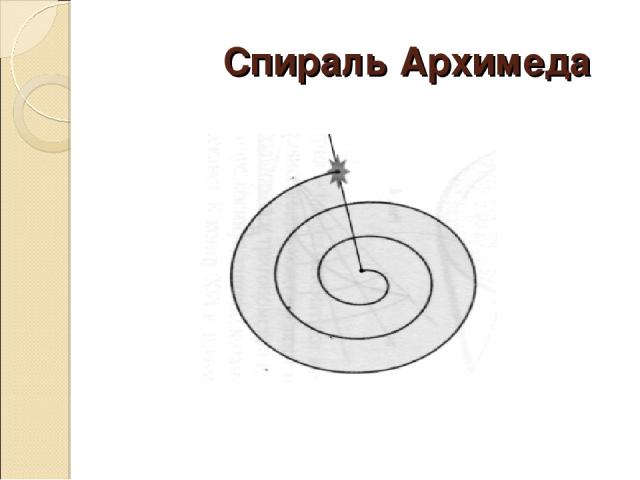
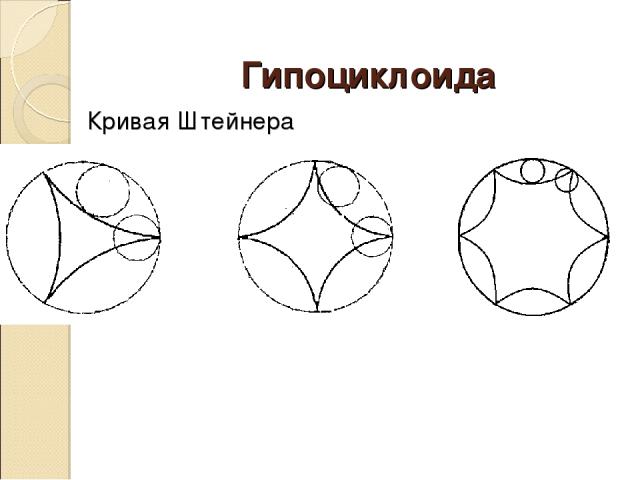
Спираль Архимеда

Спираль Архимеда - немного истории кто Архимед когда в 300 году до нашей эры При каких обстоятельствах Pаковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Форма спирально завитой раковины привлекла внимание Архимеда. Дело в том, что отношение измерений завитков раковины постоянно и равно 1.618. Архимед изучал спираль раковин и вывел уравнение спирали.  Cпираль, вычерченная по этому уравнению, называется его именем. Но мысль о спирале возникла в связи с задачей о трисекции угла Занимательные факты 1. Архимед умел проводить касательную к своей спирали. При исследовании этой спирали он находит сумму квадратов натуральных чисел. 2.Изображение геометрической фигуры под названием Архимедова спираль найдено на древнегреческом объекте, который появился более чем за тысячу лет до самого Архимеда. Находка Бронзового века принадлежит Минойской культуре. 3.С помощью спирали Архимеда может быть легко решена задача о трисекции угла

Спираль Архимеда мы видим

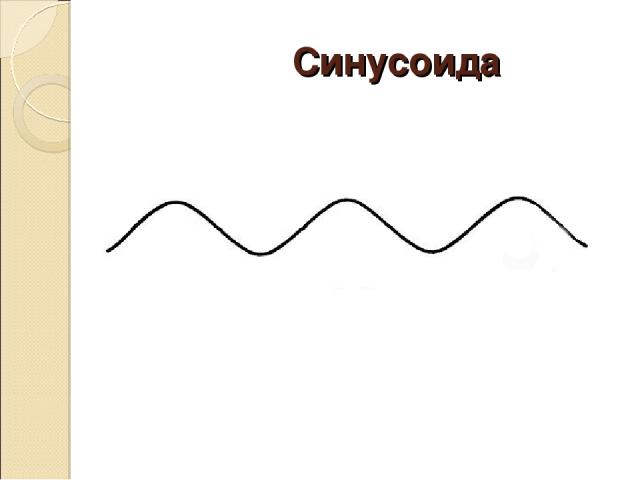
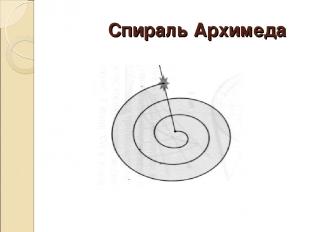
Синусоида

Синусоида – немного истории Кто Леонард Эйлер Когда в XVIII веке При каких обстоятельствах Синусоида-график функции синуса Занимательные факты На данный момент известно, что все планеты Солнечной Системы (СС) перемещаются в пространстве по кривым, в одном направлении с Солнцем. Эти кривые представляют из себя синусоиды, названые Si p (синусоидами планет). Синусоида Жабинского (СЖ) — феномен, открытый А.М. Жабинским, иллюстрирующий искусственность традиционной хронологизации древних артефактов. Согласно теории Жабинского, уровень сложности артефакта прямо зависит от номера линии «синусоиды».

Синусоиду мы видим

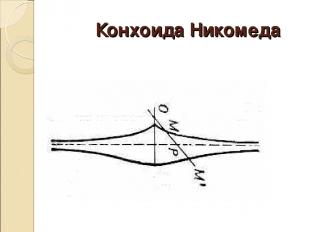
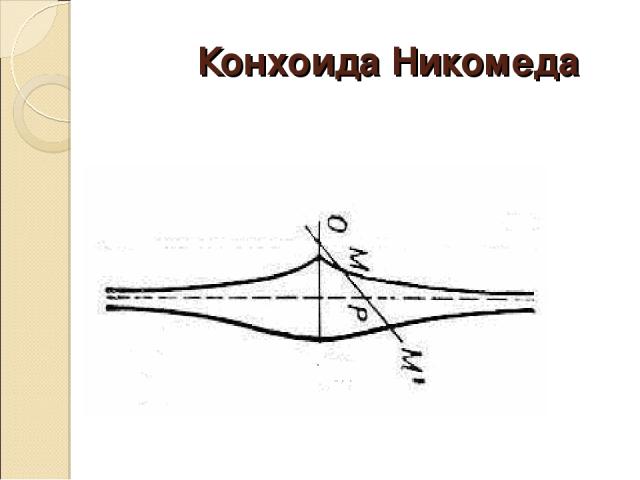
Конхоида Никомеда

Конхоида Никомеда- немного истории Кто Никомед Когда ок.250-150гг. до н.э. При каких обстоятельствах При решении задачи о трисекции угла Занимательные факты Как рассказывают источники, Никомед очень гордился этой кривой и построил прибор для ее черчения. Он применил свою кривую для решения задач об удвоении куба и трисекции угла.

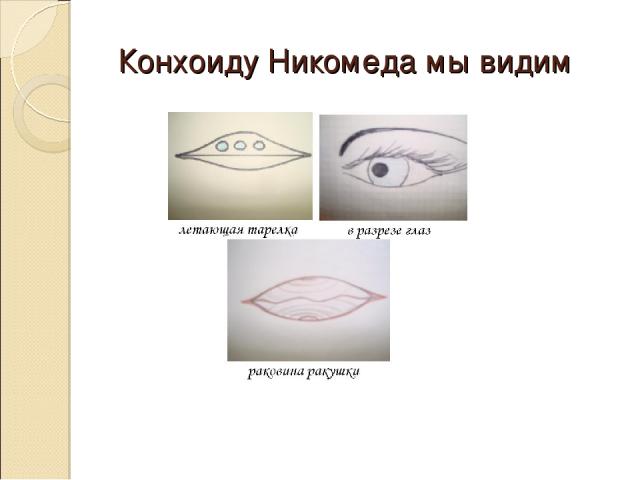
Конхоиду Никомеда мы видим

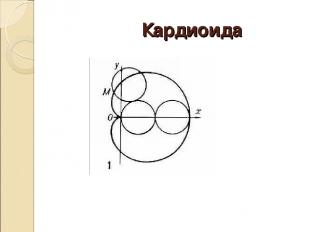
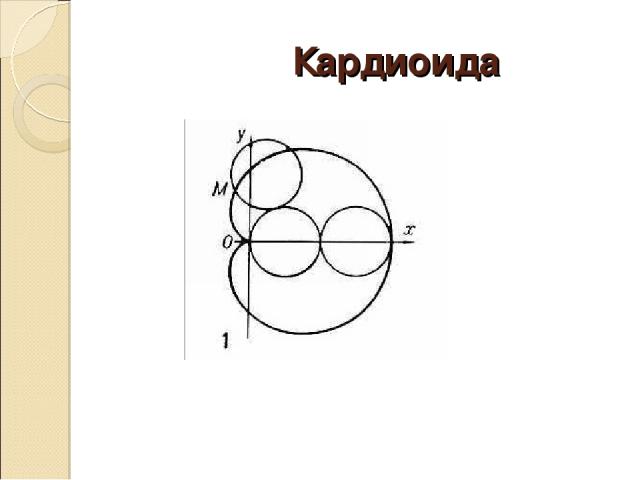
Кардиоида

Кардиоида - немного истории Кто Великий художник и математик Альбрехт Дюрер. С. Когда 1525 году При каких обстоятельствах Получила своё название из за схожести своих очертаний со стилизованным изображением сердца. Кардиоида является частным случаем улитки Паскаля, которую открыл Этьен Паскаль Занимательные факты Спустя 125 лет появились первые зубчатые колеса с эпициклоидальным профилем зуба, предложенные и изготовленные французским математиком и инженером Жюлем Дезаргом (1593–1661), а в 1694 году выполнен первый математический анализ эпициклоидального зацепления. Однако лишь в первой четверти XIX столетия точные методы расчета таких зацеплений стали достоянием инженеров-практиков.

Кардиоиду мы видим

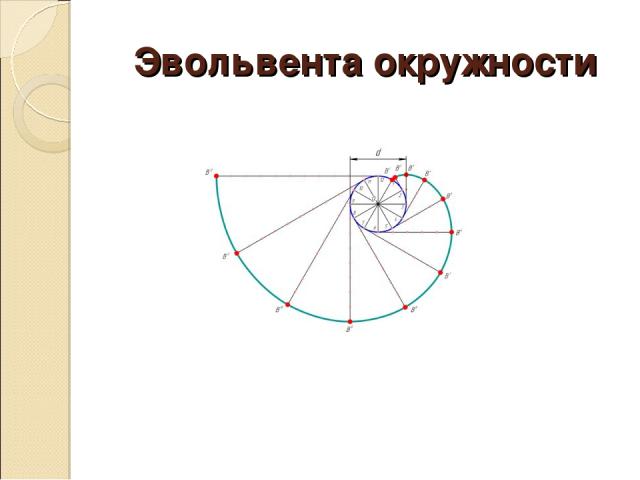
Эвольвента окружности

Эвольвента окружности– немного истории Кто великий математик и механик Леонард Эйлер. Когда в 1754 году При каких обстоятельствах Эвольвента – частный случай эпициклоиды, при которой образующая окружность перекатывается по кругу бесконечно большого радиуса, то есть по прямой линии. Занимательные факты По эвольвенте обрабатывают профиль зубьев зубчатых колёс. Эвольвента окружности всегда занимала особое положение среди важнейших специальных кривых, так как по теории эта кривая должна давать предельно точную развертку окружности при условии равенства длины расчетной дуги как части этой окружности, длине хорды, соединяющей оба конца этой расчетной дуги окружности. При этом предельно большая точность геометрических построений могла достигаться только при значительном увеличении количества частей, на которые необходимо было разделить заданную окружность.

Эвольвенту окружности мы видим В вентиляторе

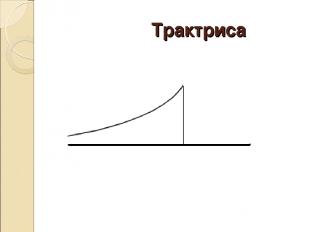
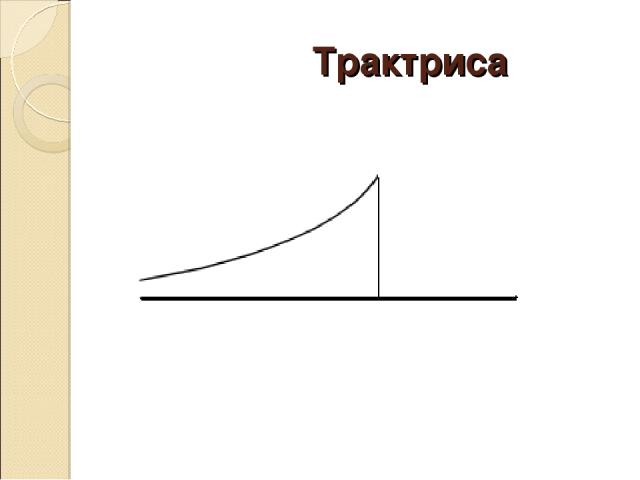
Трактриса

Трактриса – немного истории Кто Лейбниц Когда 17 век При каких обстоятельствах Задача Лейбница о трактрисе (собачьей кривой) Пусть по оси абсцисс бежит собака, а ее хозяин (первоначально находившийся на оси ординат) бежит за ней так, что поводок все время натянут. В этом случае поводок будет направлен по касательной к пути хозяина. Требуется найти, по какой линии бежит хозяин собаки. Только Лейбниц, конечно, собак не мучил, а возил по столу свои серебряные часы на цепочке Занимательные факты Через полтора столетия после открытия трактрисы она сыграла роль в утверждении неевклидовой геометрии Лобачевского: если повернуть трактрису вокруг оси абсцисс, то на полученной поверхности вращения будет выполняться геометрия Лобачевского. Если вращать трактрису, она опишет поверхность вращения, имеющую вид двух воронок, составленных своими раструбами. Это и есть псевдосфера. Самое ее интересное свойство: если на ней вырезать "заплату", то эту заплату можно будет приложить к любому другому участку псевдосферы - и она приляжет всеми своими точками. Таким же свойством обладают сфера и плоскость; только для сферы и плоскости оно очевидно, а для псевдосферы - не очень. Это и есть свойство постоянства гауссовой кривизны - положительной для сферы, нулевой для плоскости и отрицательной для псевдосферы

Трактрису мы видим

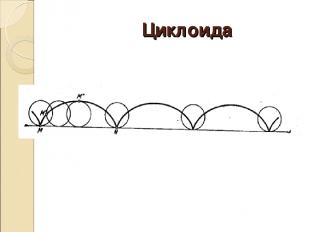
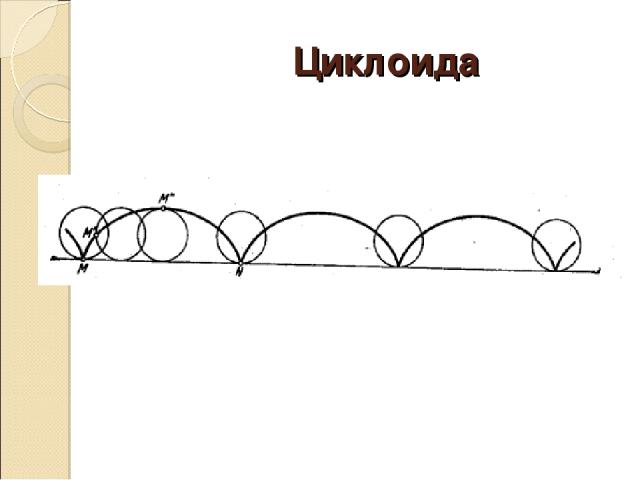
Циклоида

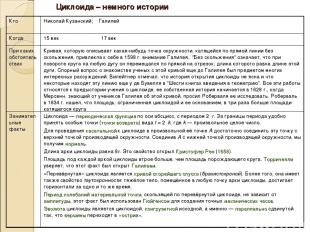
Циклоида – немного истории Кто Николай Кузанский; Галилей Когда 15 век 17 век При каких обстоятельствах Кривая, которую описывает какая-нибудь точка окружности, катящейся по прямой линии без скольжения, привлекла к себе в 1598 г. внимание Галилея,. "Без скольжения" означает, что при повороте круга на любую дугу он перемещался по прямой на отрезок, длина которого равна длине этой дуги. Спорный вопрос о знакомстве ученых с этой кривой еще до Галилея был предметом многих интересных рассуждений. Вилейтнер отмечал, что история открытия циклоиды не ясна и что некоторые находят эту линию еще у де Бувелля в "Шести книгах введения в геометрию". Все эти работы относятся к предыстории учения о циклоиде, ее собственная история начинается в 1628 г., когда Мерсенн, знающий от учеников Галилея об этой кривой, просил Роберваля ее исследовать. Роберваль в 1634 г. нашел, что площадь, ограниченная циклоидой и ее основанием, в три раза больше площади катящегося круга Занимательные факты Циклоида — периодическая функция по оси абсцисс, с периодом 2πr. За границы периода удобно принять особые точки (точки возврата) вида t = 2πk, где k — произвольное целое число. Для проведения касательной к циклоиде в произвольной её точке A достаточно соединить эту точку с верхней точкой производящей окружности. Соединив A с нижней точкой производящей окружности, мы получим нормаль. Длина арки циклоиды равна 8r. Это свойство открыл Кристофер Рен (1658). Площадь под каждой аркой циклоиды втрое больше, чем площадь порождающего круга. Торричелли уверяет, что этот факт был открыт Галилеем. «Перевёрнутая» циклоида является кривой скорейшего спуска (брахистохроной). Более того, она имеет также свойство таутохронности: тяжёлое тело, помещённое в любую точку арки циклоиды, достигает горизонтали за одно и то же время. Период колебаний материальной точки, скользящей по перевёрнутой циклоиде, не зависит от амплитуды, этот факт был использован Гюйгенсом для создания точных механических часов. Эволюта циклоиды является циклоидой, конгруэнтной исходной, а именно — параллельно сдвинутой так, что вершины переходят в «острия».

Циклоиду мы видим

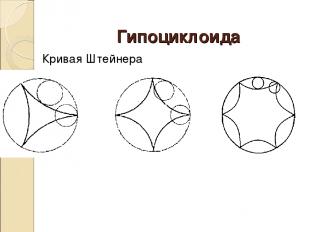
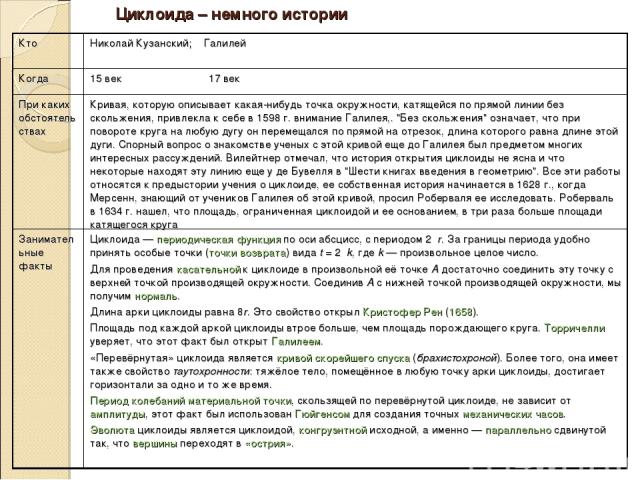
Гипоциклоида Кривая Штейнера Астроида

Гипоциклоида – дельтоида, плоская кривая, описываемая фиксированной точкой окружности, катящейся по внутренней стороне другой окружности, радиус которой втрое больше радиуса первой. Кто Л.Эйлер Э.Штейнер Когда 18 век 19 век При каких обстоятельствах Название кривая получила за сходство с греческой буквой Δ. Занимательные факты Рассмотрим теперь гипоциклоиды, описываемые кругом радиуса г, когда он катится внутри большого круга радиуса R. Если отношение R/r равно 2, 3, 4, ..., то наша кривая будет иметь R/r точек возврата. Если, например, R/r равно 3, то мы получаем так называемую дельтоиду с тремя точками возврата . Точно такую же дельтоиду мы получим, если отношение R/r равно 3/2, т. е. если (радиус катящегося круга составляет 2/з радиуса неподвижного круга. При этом отрезки касательных к дельтоиде прямых, концы которых лежат на нашей кривой, будут иметь одну и ту же длину. В случае если отношение R/r равно 4 или 4/з, мы получаем астроиду с четырьмя точками возврата . Полученный результат можно обобщить на аналогичные гипоциклоиды высших порядков, а именно: если отношение R/r равно п или п/(п—1), то катящийся круг будет давать нам соответствующую кривую с п точками возврата. Интересный результат получается, когда отношение R/r оказывается равным 2 . В этом случае гипоциклоида вырождается в прямую линию, совпадающую с диаметром большого круга, причем оба ее конца можно рассматривать как вырожденные  точки возврата

Гипоциклоиду мы видим