Презентация на тему: Решение транспортной задачи в среде Maple

Гимназия №125Советского района РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИ В СРЕДЕ MAPLE Выполнила: ученица 11М класса Владимирова О.М.Руководители: К.Ф.-М.Н., доцент КГПУ, заслуженный учитель РТ Салехова Л.Л.учитель математики гимназии № 125Чикрин Е. А.Казань2005

Содержание Формулировка транспортной задачиМатематическая модель транспортной задачиНеобходимое и достаточное условия разрешимости транспортной задачиОпорное решение транспортной задачи. ЦиклыПостроение начального опорного решения методом минимальной стоимостиПереход от одного опорного решения к другомуМетод потенциаловРешение транспортной задачи методом потенциаловРешение транспортной задачи в среде Maple

Формулировка транспортной задачи

Формулировка транспортной задачи А=(а1, а2, ..., аm)В=(b1, b2, ..., bn)

Математическая модель транспортной задачи

Математическая модель транспортной задачи

Математическая модель транспортной задачи Z (X) = 3x11 + 5x12 + 7x13 + 4x21 + 6x22 + 10x23

Необходимое и достаточное условия разрешимости транспортной задачи Теорема. Для того чтобы транспортная задача линейного программирования имела решение, необходимо и достаточно, чтобы суммарные запасы поставщиков равнялись суммарным запасам потребителей:т.е. задача должна быть с правильным балансом. Ранг системы векторов-условий транспортной задачи равен N =m +n –1.

Опорное решение транспортной задачи. Циклы Теорема (о взаимосвязи линейной зависимости векторов-условий и возможности образования цикла). Для того, чтобы система векторов-условий транспортной задачи была линейно зависимой, необходимо и достаточно, чтобы из соответствующих клеток таблицы можно было выделить часть, которая образует цикл. Следствие. Допустимое решение транспортной задачи X = (xij), i =1, 2, ..., m, j =1, 2, ..., n является опорным тогда и только тогда, когда из занятых им клеток таблицы нельзя образовать ни одного цикла.

Построение начального опорного решения методом минимальной стоимости Теорема. Решение транспортной задачи, построенное методом минимальной стоимости, является опорным.

Построение начального опорного решения методом минимальной стоимости Число занятых клеток таблицы равно N =m +n –1=3+2–1=4.

Переход от одного опорного решения к другому Теорема ( о существовании и единственности цикла). Если таблица транспортной задачи содержит опорное решение, то для любой свободной клетки таблицы существует единственный цикл, содержащий эту клетку и часть клеток, занятых опорным решением. Цикл называется означенным, если его угловые клетки пронумерованы по порядку и нечетным клеткам приписан знак «+», а четным знак «–».

Переход от одного опорного решения к другому Сдвигом по циклу на величину называется увеличение объемов перевозок во всех нечетных клетках цикла, отмеченных знаком «+», на и уменьшение объемов перевозок во всех четных клетках, отмеченных знаком «–», на . Теорема. Если таблица транспортной задачи содержит опорное решение, то при сдвиге по любому циклу, содержащему одну свободную клетку, на величину = {хij} получится опорное решение.

Метод потенциалов Теорема (признак оптимальности опорного решения). Если допустимое решение X = (xij ), i = 1, 2, ..., m, j = 1, 2, ..., n транспортной задачи является оптимальным, то существуют потенциалы (числа) поставщиков ui, i = 1, 2, …, m и потребителей vj, j = 1, 2, …, n, удовлетворяющие следующим условиям: ui + vj = cij при xij > 0, ui + vj ≤cij при xij = 0.ij = ui +vj –cij при xij =0 Опорное решение является оптимальным, если для всех векторов-условий (клеток таблицы) оценки неположительные.

Решение транспортной задачи методом потенциалов

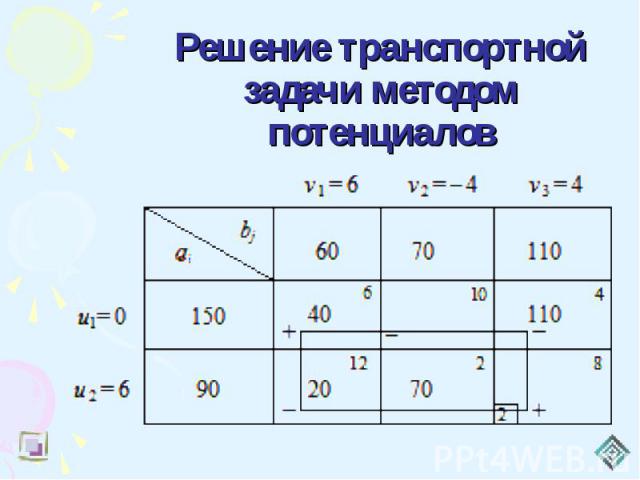
Решение транспортной задачи методом потенциалов Z (Х1) = 40*6+110*4+20*12+70*2 = 1060

Решение транспортной задачи методом потенциалов 12 = u1 +v2 –c12 = 0–4–10 = –1423 = u2 +v3 –c23 = 6+4–8 = 2.

Решение транспортной задачи методом потенциалов

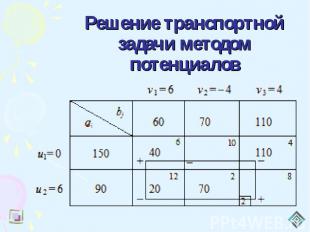
Решение транспортной задачи методом потенциалов

Решение транспортной задачи методом потенциалов Z (Х2) = 60 *6+90 *4+70 *2+20 *8 = 1020

Решение транспортной задачи в среде Maple standardize – приведение заданной системы уравнений или неравенств к стандартной форме неравенств типа «меньше или равно». minimize - вычисление минимума функции;simplify (expr, n1, n2, …) – возвращает упрощенное выражение expr с учетом параметров с именами n1, n2, … (в том числе заданных списком или множеством);

Решение транспортной задачи в среде Maple Для решения транспортной задачи в программе Maple 7 имена ячеек должны быть указаны в виде х11, х12 и т.д.

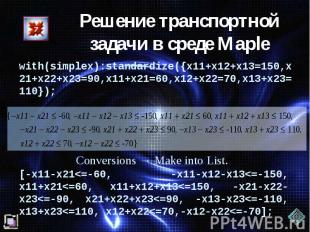
Решение транспортной задачи в среде Maple with(simplex):standardize({x11+x12+x13=150,x21+x22+x23=90,x11+x21=60,x12+x22=70,x13+x23=110});[-x11-x21<=-60, -x11-x12-x13<=-150, x11+x21<=60, x11+x12+x13<=150, -x21-x22-x23<=-90, x21+x22+x23<=90, -x13-x23<=-110, x13+x23<=110, x12+x22<=70,-x12-x22<=-70];

Решение транспортной задачи в среде Maplewith(simplex):minimize(6*x11+10*x12+4*x13+12*x21+2*x22+8*x23,{-x11-x21<=-60, -x11-x12-x13<=-150, x11+x21<=60, x11+x12+x13<=150, -x21-x22-x23<=-90, x21+x22+x23<=90, -x13-x23<=-110, x13+x23<=110, x12+x22 <=70, -x12-x22<=-70}, NONNEGATIVE);simplify(6*x11+10*x12+4*x13+12*x21+2*x22+8*x23, [x13=90, x22=70, x23=20, x11=60, x12=0, x21=0]);

Огромное спасибо!!!