Презентация на тему: Правило суммы. Правило произведения.

Правило суммы. Правило произведения. Автор учитель высшей квалификационной категории МБОУ «Лицей №52» г. Рязань Игошина Л.М.

Два уровня решения комбинаторных задач. 1. Найти хотя бы одно решение или доказать, что его нет. Если в n клетках сидит n+1 или больше кроликов, то найдётся клетка, в которой сидят по крайней мере два кролика.
Два уровня решения комбинаторных задач. 2. Если решений много, то посчитать их количество и выбрать оптимальное .

Сколько человек участвовало в прогулке, если известно, 16 из них взяли бутерброд с ветчиной, 24 – с колбасой, 15 – с сыром, 11 – с ветчиной и колбасой, 8 – с ветчиной и сыром, 12 – с колбасой и сыром, 6 человек – бутерброды всех видов и 6 человек взяли пирожки.

В отделе научно – исследовательского института работают несколько человек, причем каждый из них знает хотя бы один иностранный язык: 6 человек знают английский язык, 6 – немецкий, 7 – французский , 4 – английский и немецкий, 3 – немецкий и французский, 2 – французский и английский, 1 человек знает все три языка. Сколько человек работают в отделе? Сколько из них знает только английский язык? Сколько человек знают только один язык?

Киев Чернигов Новгород – Сиверский

Сколько четырехзначных чисел можно составить из цифр 0,1,2,3,4.5, если : а) ни одна цифра не повторяется; б) цифры могут повторяться; в) число нечетное и цифры могут повторяться.

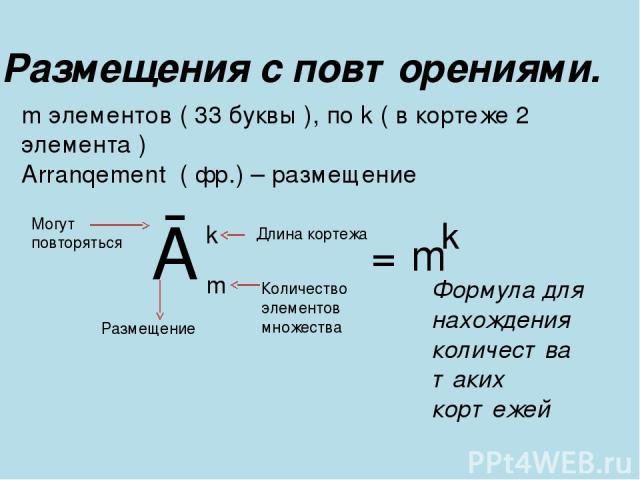
Из 33 букв русского алфавита составить все возможные слова, состоящие из 2 – х букв, из 3 – букв.
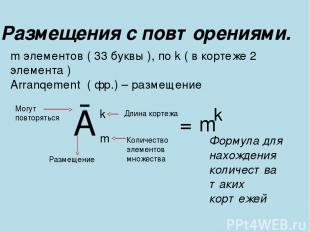
Размещения с повторениями. m элементов ( 33 буквы ), по k ( в кортеже 2 элемента ) Arranqement ( фр.) – размещение Ā m k Могут повторяться Длина кортежа Количество элементов множества Размещение = m k Формула для нахождения количества таких кортежей

Есть конфеты 9 видов. Сколько различных наборов по 5 конфет можно составить ?

№ 422. Сколько существует пятизначных номеров, не содержащих цифру 8? Не содержащих цифры 8 и 0 ? Составленных из цифр 2,3,5,7?

Размещения без повторений. A k m = ____ m! ( m – k ) !

№ 426. Сколькими способами можно составить трехцветный флаг, если имеются ткани пяти различных цветов? Решите эту задачу при условии, что одна полоса должна быть красной. № 428. Из 10 различных книг выбирают 4 для посылки. Сколькими способами это можно сделать?

Перестановки . Permutation ( фр .) – перестановки Р m = m! №432. Сколькими способами могут расположиться в турнирной таблице 10 футбольных команд, если известно, никакие две команды не набрали одинаковое количество очков?

Домашнее задание . Подготовка к самостоятельной работе. Стр.228 № 423,429, 431.