Презентация на тему: Построение сечений многогранников

Урок обобщения и систематизации знаний учащихся по геометрии в 10 классе. МОУ «Инсарская средняя общеобразовательная школа №1» Чудаева Елена Владимировна, г. Инсар, Республика Мордовия

Что изучает стереометрия ? Стереометрия знакомит с разнообразием геометрических тел, формирует необходимые пространственные представления. Стереометрия дает метод научного познания, способствует развитию логического мышления. Стереометрия – сама по себе очень интересна. Она имеет яркую историю, связанную с именами знаменитых ученых

"Те, кто влюбляются в практику без теории, уподобляются мореплавателю, садящемуся на корабль без руля и компаса и потому никогда не знающему, куда он плывет".          Леонардо да Винчи http://blogs.nnm.ru/page6/

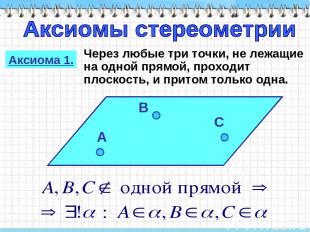
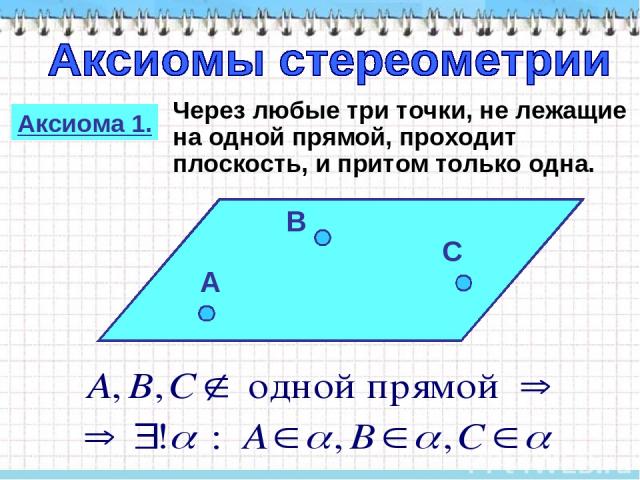
Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

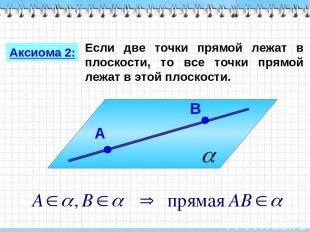
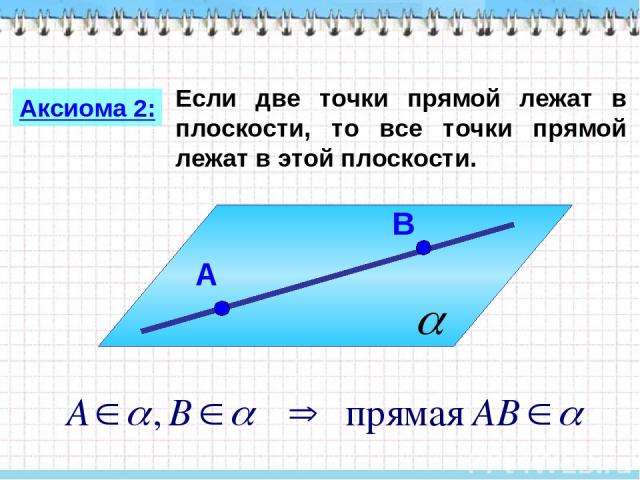
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. Аксиома 2:

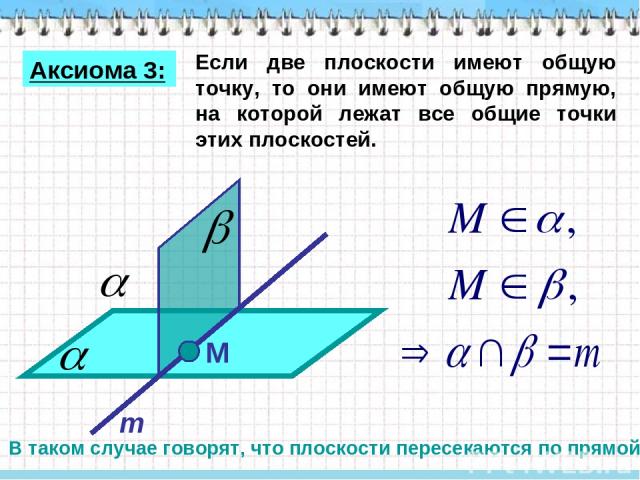
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Аксиома 3: В таком случае говорят, что плоскости пересекаются по прямой

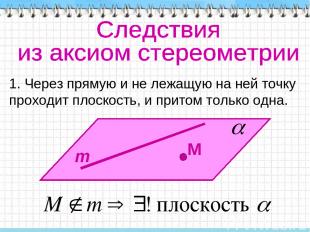
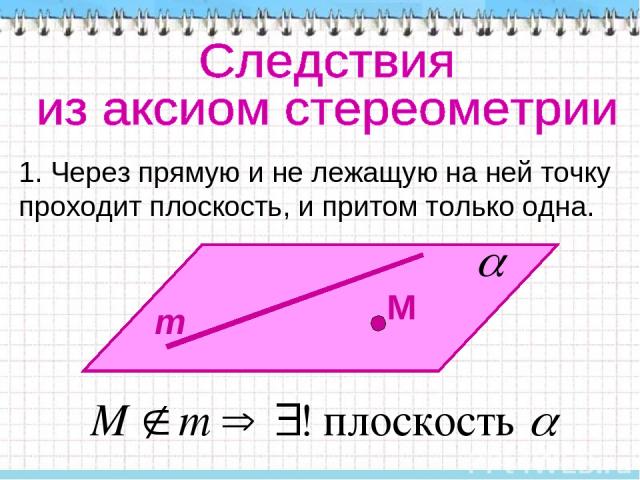
1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

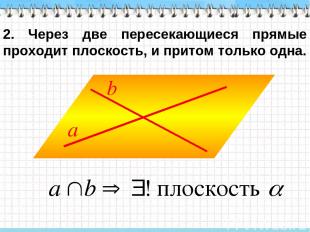
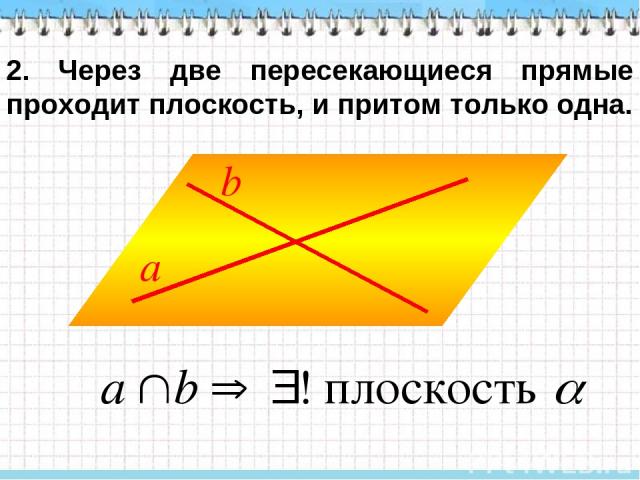
2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Две прямые лежат в одной плоскости 2. Прямые пересекаются 1. Прямые параллельны Одна общая точка Нет общих точек

Не лежат в одной плоскости: являются скрещивающимися m

1. Прямая лежит в плоскости 2. Прямая пересекает плоскость Бесконечно много общих точек Одна общая точка

3. Прямая параллельна плоскости. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости. Нет общих точек Признак параллельности прямой и плоскости:

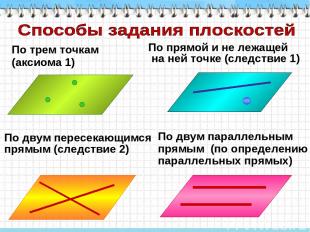
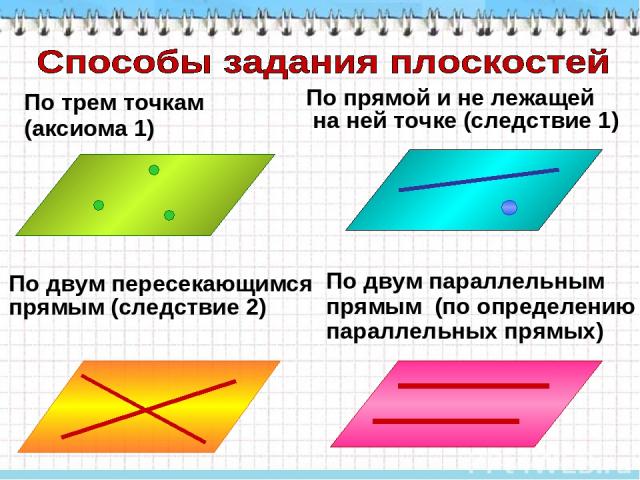
По трем точкам (аксиома 1) По прямой и не лежащей на ней точке (следствие 1) По двум пересекающимся прямым (следствие 2) По двум параллельным прямым (по определению параллельных прямых)

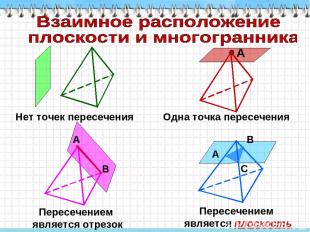
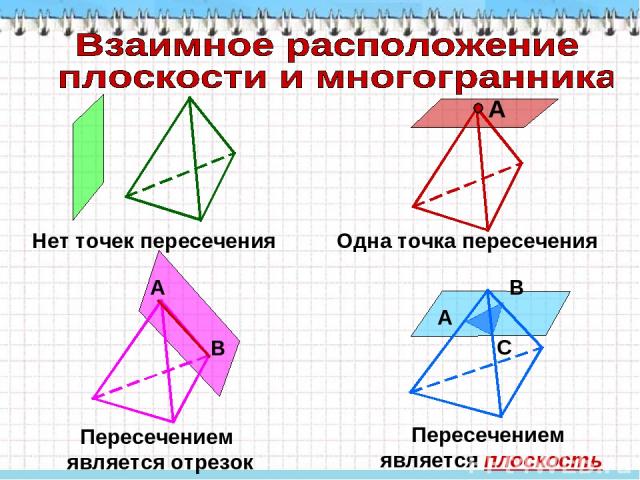
В А Нет точек пересечения Одна точка пересечения Пересечением является отрезок Пересечением является плоскость

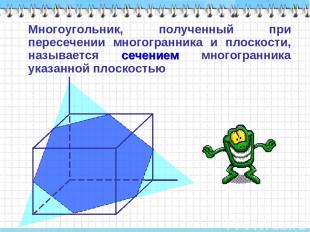
Многоугольник, полученный при пересечении многогранника и плоскости, называется сечением многогранника указанной плоскостью

Умение решать задачи – практическое искусство, подобное плаванию, или катанию на лыжах … : научиться этому можно лишь подражая избранным образцам и постоянно тренируясь.. Д. Пойа

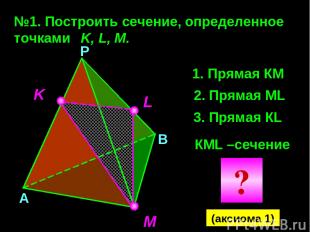
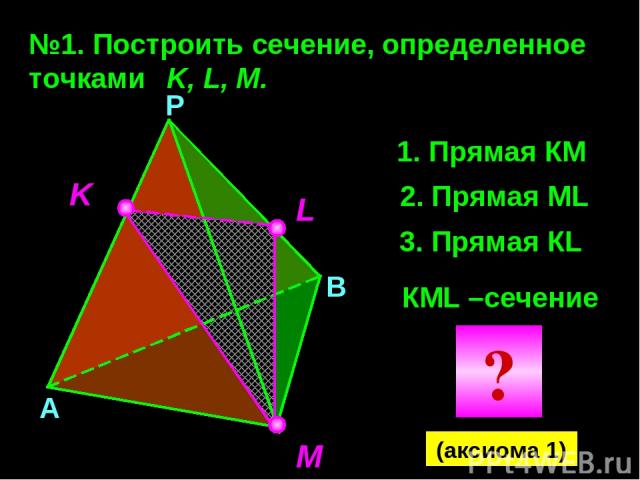
№1. Построить сечение, определенное точками K, L, M. K M L Прямая КМ 2. Прямая МL 3. Прямая КL КМL –сечение А В Р (аксиома 1) ?

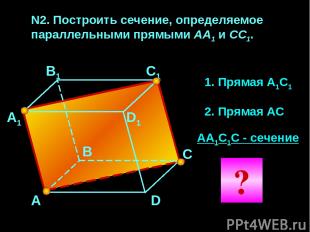
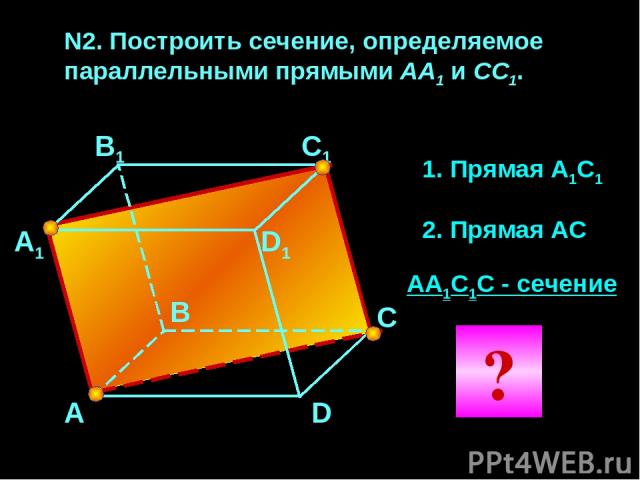
N2. Построить сечение, определяемое параллельными прямыми АА1 и CC1. А А1 В1 С1 D1 С В D 1. Прямая А1С1 2. Прямая АС АА1С1С - сечение ?

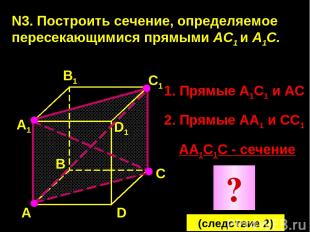
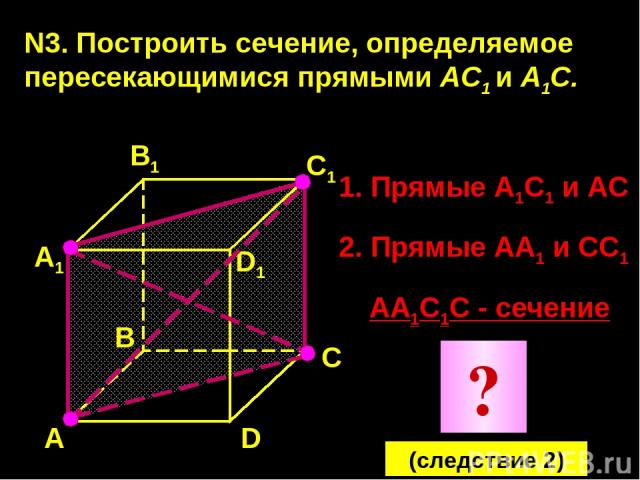
N3. Построить сечение, определяемое пересекающимися прямыми АС1 и А1С. А А1 В1 С1 D1 D В С 1. Прямые А1С1 и АС 2. Прямые АА1 и СС1 АА1С1С - сечение ? (следствие 2)

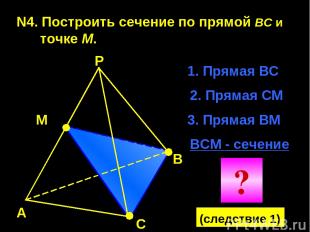
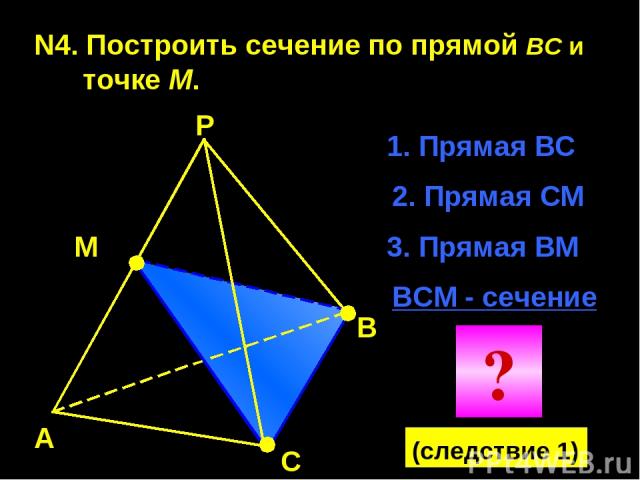
N4. Построить сечение по прямой BC и точке М. А В С Р М 1. Прямая ВС 2. Прямая СМ ВСМ - сечение 3. Прямая ВМ ? (следствие 1)

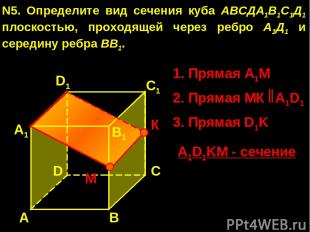
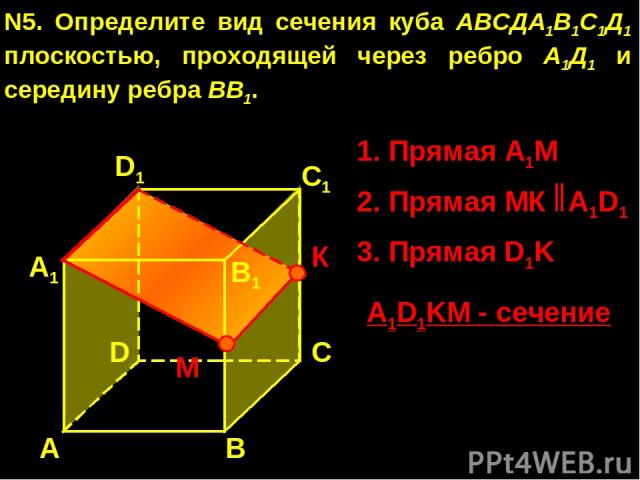
А А1 В1 С1 D1 D С N5. Определите вид сечения куба АВСДА1В1С1Д1 плоскостью, проходящей через ребро А1Д1 и середину ребра ВВ1. В 1. Прямая А1М 3. Прямая D1K A1D1KM - сечение

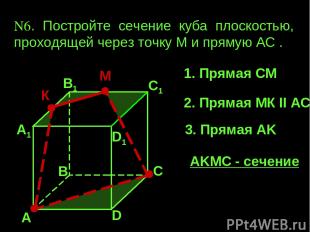
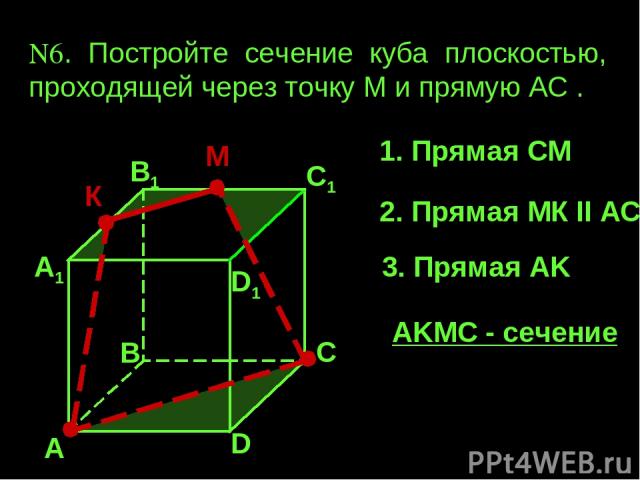
А А1 В1 С1 D1 D В С N6. Постройте сечение куба плоскостью, проходящей через точку М и прямую АС . М 1. Прямая СМ 2. Прямая МК II AC 3. Прямая AK AKМС - сечение

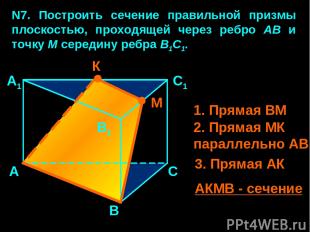
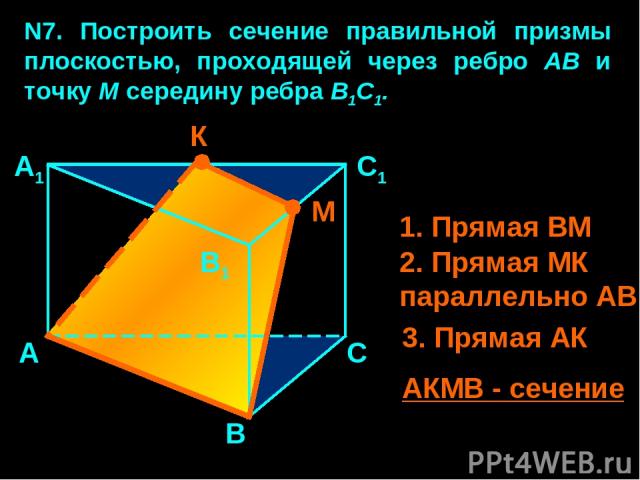
N7. Построить сечение правильной призмы плоскостью, проходящей через ребро АВ и точку М середину ребра В1С1. А В С А1 В1 С1 М 1. Прямая ВМ 2. Прямая МК параллельно АВ 3. Прямая АК АКМВ - сечение

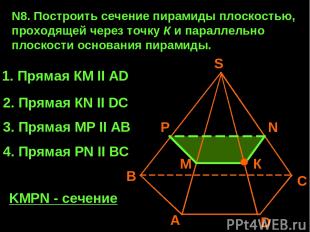
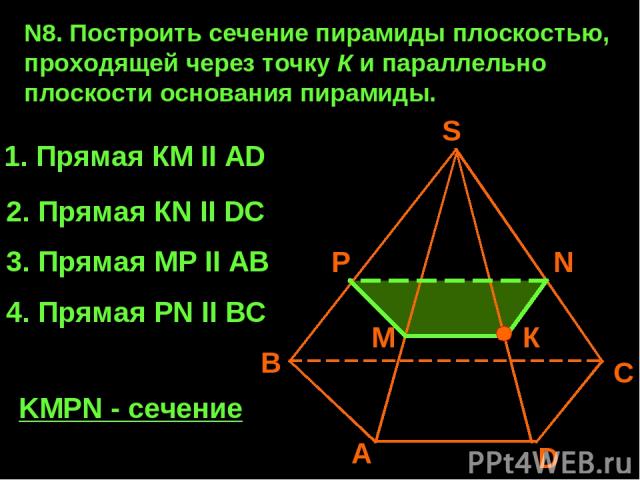
N8. Построить сечение пирамиды плоскостью, проходящей через точку К и параллельно плоскости основания пирамиды. А В С D К S 1. Прямая КМ II AD 2. Прямая КN II DC N M 3. Прямая МP II AB P 4. Прямая PN II BC KMPN - сечение

МЕТОД СЛЕДОВ Суть метода: построение вспомогательной прямой, являющейся линией пересечения секущей плоскости с плоскостью грани фигуры. Эту линию называют следом секущей плоскости. Просмотр учебного видеофильма.

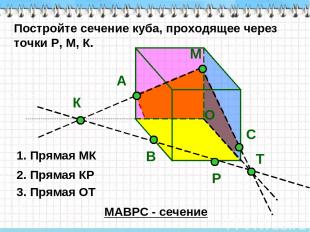
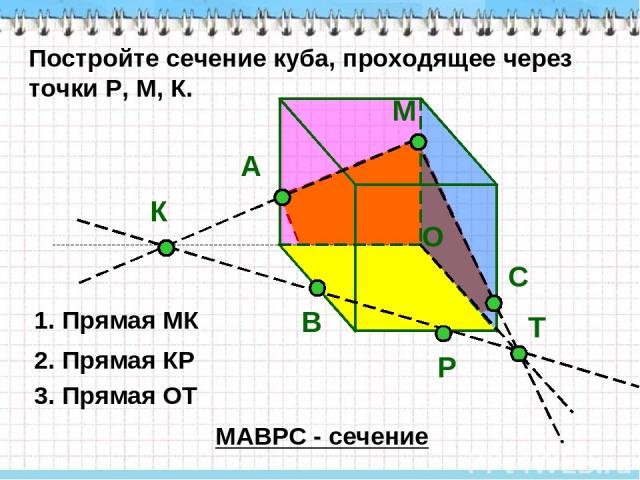
М Р Постройте сечение куба, проходящее через точки P, М, К. К А 1. Прямая МК В 2. Прямая КР О Т 3. Прямая ОТ МАВРС - сечение С

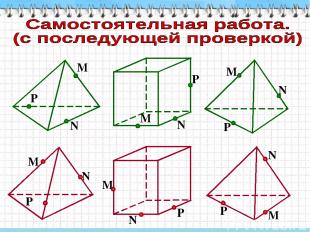
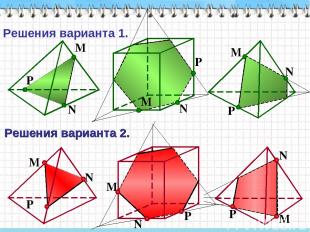
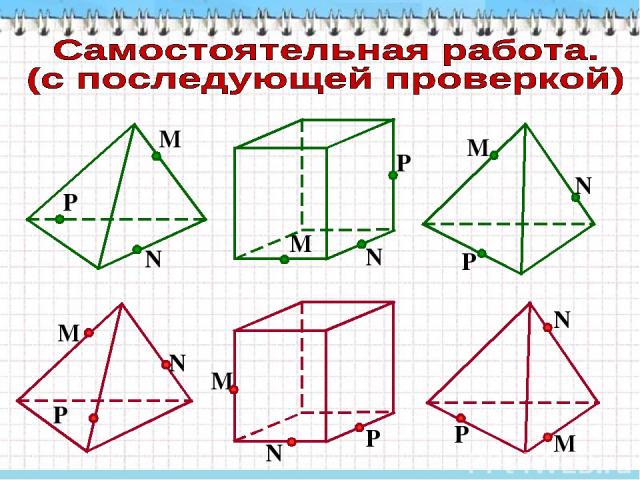
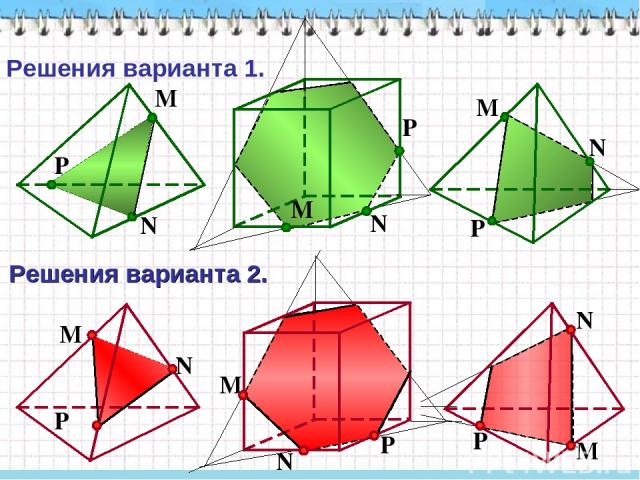
P N M N P M N P M Решения варианта 1. Решения варианта 2. M N P M N P M N P

Составить две задачи на построение сечений многогранников с использованием полученных знаний.

Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их (Д. Пойа)

ЛИТЕРАТУРА 1. Электронное издание «1С: Школа. Математика, 5-11 кл. Практикум» 2. Электронное издание «Решебник по геометрии. Пособие для абитуриентов. Полный курс за 7-11 классы» 3. Атанасян Л.С. и др. Геометрия. Учебник для 10-11 классов общеобразовательных учреждений Изображение с сайта: http://www.cdvseti.ru/id3700.html Анимация с сайта: http://badbad-girl.narod.ru/zelenie.html Портреты математиков взяты с диска "Математика 5-11". Изображение с сайта: http://www.thg.ru/education/20050714/images/arhimed_cut.jpg