Презентация на тему: ПЛТ

Финансовая функция "ПЛТ" в MS Excel

ПЛТ — одна из финансовых функций, возвращающая сумму периодического платежа для аннуитета на основе постоянства сумм платежей и постоянной процентной ставки.

Синтаксис: ПЛТ(ставка; кпер; пс; [бс]; [тип])

Ставка - процентная ставка за период займа. Например, при годовой процентной ставке в 6% для квартальной ставки используйте значение 6%/4 Кпер - общее число периодов выплат по займу Пс - приведенная (нынешняя) стоимость - общая сумма, на настоящий момент равноценная серии будущих выплат. Бс - будущая стоимость или баланс наличности, который нужно достичь после последней выплаты; принимается равной 0, если значение не указано. Тип - логическое значение (0 или 1), обозначающее, должна ли производиться выплата в конце периода(0 или отсутствие значения) или в начле периода(1)

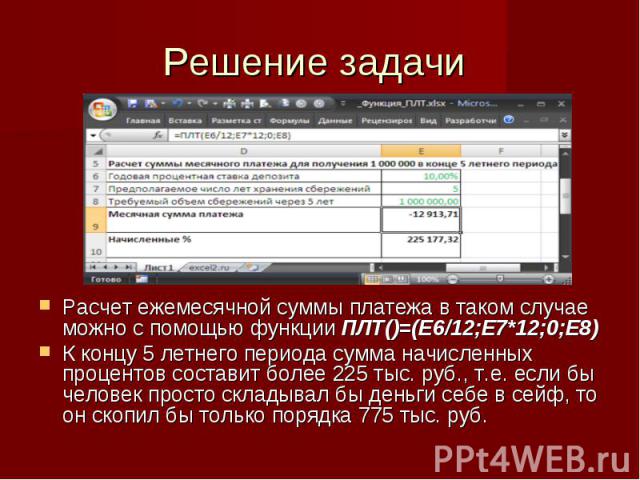
Пример задачи по функции “ПЛТ” Предположим человек планирует ежемесячно откладывать деньги, чтобы скопить через 5 лет (ячейка E7) 1 млн. рублей (E8). Деньги ежемесячно он планирует относить в банк и пополнять свой вклад. В банке действует процентная ставка 10% (E6) и человек пологает, что она будет действовать без изменений в течение 5 лет. Какую сумму человек должен ежемесячно относить в банк чтобы таким образом через 5 лет скопить 1 млн. руб. ?

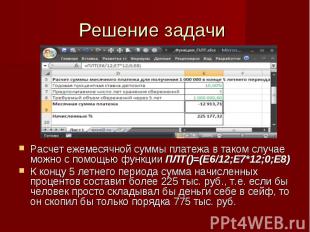
Решение задачи Расчет ежемесячной суммы платежа в таком случае можно с помощью функции ПЛТ()=(E6/12;E7*12;0;E8) К концу 5 летнего периода сумма начисленных процентов составит более 225 тыс. руб., т.е. если бы человек просто складывал бы деньги себе в сейф, то он скопил бы только порядка 775 тыс. руб.

Конец! Спасибо за внимание!