Презентация на тему: Несколько способов решений задач школьного курса

Муниципальное образовательное учреждение«Средняя общеобразовательная школа №19 г.Владивостока» «Несколько способов решений задач школьного курса» Работа ученицы 8в класса,МОУ СОШ №19Михайлюк Елизаветы ВячеславовныРуководительучитель математики школы №19, Мацюк Надежда Владимировна.

Введение. Философия записана в огромной книге, раскрытой перед нашими глазами. Однако нельзя понять книгу, не зная языка и не различая букв, которыми она написана. Написана же она на языке математики, а ее буквы – это треугольники, четырехугольники, круги, шары, конусы, пирамиды и другие геометрические фигуры, без помощи которых ум человеческий не может понять в ней ни слова; без них мы можем лишь наугад блуждать по темному лабиринту. Галилео Галилей 

С древнейших времён люди интересовались различными математическими преобразованиями. Задачи, связанные с уравнениями, решались ещё в Древнем Египте и Вавилоне. Теория уравненийинтересовала и интересует математиков всех времён и народов. Первые общие утверждения о тождественные преобразования встречаются у древнегреческих математиков, начиная с VI в. до н.э. Среди математиков древней Греции было принято выражать все алгебраические утверждения в геометрической форме. Вместо сложения чисел говорили о добавлении отрезков, произведение двух чисел истолковывали как площадь прямоугольника, а произведение трех чисел как объем прямоугольного параллелепипеда. Алгебраические формулы принимали вид соотношений между площадями и объемами.

Старинная задача.(№157 учебник Алгебра – 7, под ред. С.А. Теляковского, М.: Просвящение, 2009г)  Послан человек из Москвы в Вологду и велено ему проходить всякий день по 40 верст. На следующий день вслед ему был послан другой человек и велено ему проходить по 45 верст в день. Через сколько дней второй догонит первого? Эту задачу можно решить несколькими способами.  Алгебраический способ.45х = (х+1)4045х = 40х + 4045х – 40х = 405х = 40Х = 40 : 5Х = 8Ответ: 8 

Геометрический способ.

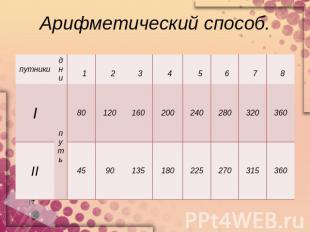
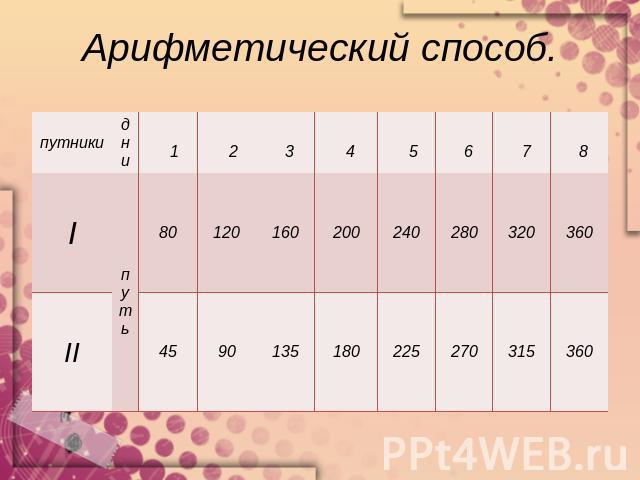
Арифметический способ.

Графический способ. Строим две прямые:у = 45х и у = 40х + 40В точке пересечения этих прямых опускаем перпендикуляр на ось х.В нашем случае мы получили число 8.

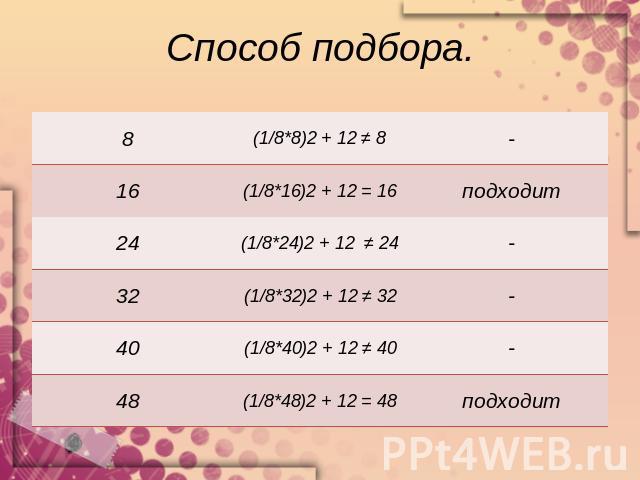
Старинная задача.(№569 учебник Алгебра – 8, под ред. С.А. Теляковского, М.: Просвящение, 2009г) Стая обезьян забавляется. Восьмая часть их в квадрате резвится в лесу. Остальные двенадцать кричат на вершине холма. Скажи мне, сколько всего обезьян? Алгебраический способ.(х)2 + 12 = х(х)2 – х + 12 = 0х2 – х +12 = 0 | 8а = 1, b = -64, с = 768b - четное, b = 2 ∙ (-32), k = -32D = k2 – acD = (-32)2 -1 ∙ 768 == 1024 – 768 = 256 = 16 х = х1 = 32 – 16 = 16х2 = 32 + 16 = 48Ответ: 16 или 48.

Способ подбора.

Графический способ. Поступаем аналогично предыдущей задаче и получаем числа 16 и 48.

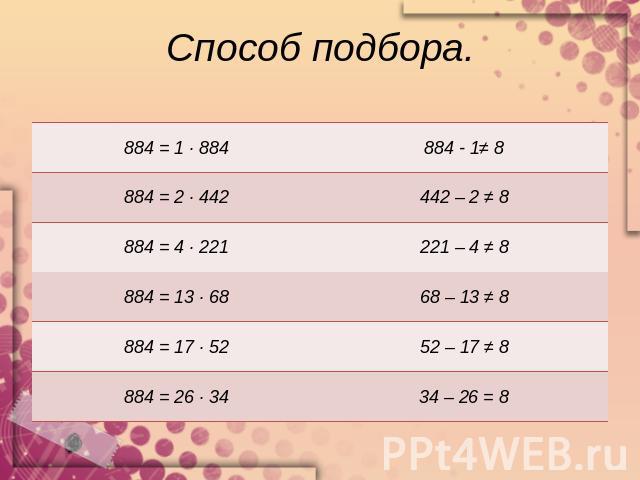
Задача.(№568 учебник Алгебра – 8, под ред. С.А. Теляковского, М.: Просвящение, 2009г)В кинотеатре число мест в ряду на 8 больше числа рядов. Сколько рядов в кинотеатре, если всего в нем имеется 884 места? Алгебраический способ.(8 + х) х = 884х2 + 8х – 884 = 0а = 1, b = 8, c = -884b – четное, b = 2 ∙ 4, k = 4D = k2 – acD = 42 – 1 ∙ - (884) = 16 + 884 = 900 = 30х = х1 = - 4 + 30 = 26х2 = - 4 – 30 = -34 – не удовлетворяет условию задачиОтвет: 26 рядов.

Геометрический способ. На сторонах квадрата со стороной х, а следовательно S=х2, строятся прямоугольники так, что другая сторона каждого из них равна 2, (т.е четверть от b). Площадь каждого прямоугольника равна 2 х. Полученную фигуру дополняют до нового квадрата, достраивая в углах четыре равных квадрата, сторона каждого из них равна 2, а площадь 4. Площадь квадрата можно представить как сумму площадей: S= x2 + 8x + 16. Заменяя х2 + 8х числом 884, получим S = 884 + 16 = 900, откуда следует, что сторона большего квадрата = 30 ( = 30). Для искомой стороны х первоначального квадрата получим х = 30 – 2 – 2 = 26.

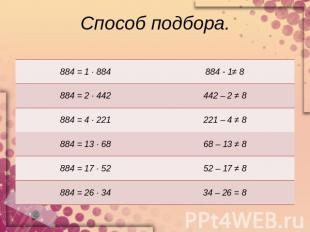
Способ подбора.

Графический способ.

Вывод. Я могу для себя сделать вывод: из всех изученных мною способов, алгебраический способ является для меня наиболее удобным и понятным. Но теперь я также могу решать задачи и другими способами и рассказать о них своим одноклассникам. Желающие могут ознакомиться с моей работой и выбрать способ, который наиболее удобен им. Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели. А. Маркушевич

Используемая литература. 1. Дроздов В.Квадратное уравнение: варианты решения.Математика (приложение к газете «Первое сентября» №10/97; с.6 )2. Окунев А.К.Квадратные функции, уравнения и неравенства. М.«Просвещение»;1972.143с.3. Панкратова Л.Квадратные уравнения. Математика (приложение к газете«Первое сентября»№21/96; с.5-6 ).4. Плужников И. Десять способов решения квадратных уравнений. Математика (приложение к газете «Первое сентября» №40/2000; с.24 -31).5. Шаталова С.Квадратные уравнения. Способы решения. Математика (приложение к газете «Первое сентября» №21/96; с. 9 - 11 ).6. Учебник «Алгебра – 7кл.» под ред. С.А. Теляковского, М.: «Просвящение», 2009г.7. Учебник «Алгебра – 8кл.» под ред. С.А. Теляковского, М.: «Просвящение», 2009г.