Презентация на тему: Метод координат

Автор: Елена Юрьевна Семёнова Метод координат в пространстве

Разложение вектора по трём некомпланарным векторам причем коэффициенты разложения x, y, z определяются единственным образом. Любой вектор а можно разложить по координатным векторам, т.е. представить в виде Коэффициенты x, y, z в разложении вектора а по координатным векторам называются координатами вектора а в данной системе координат.

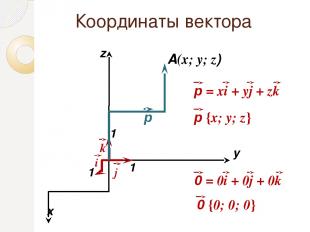
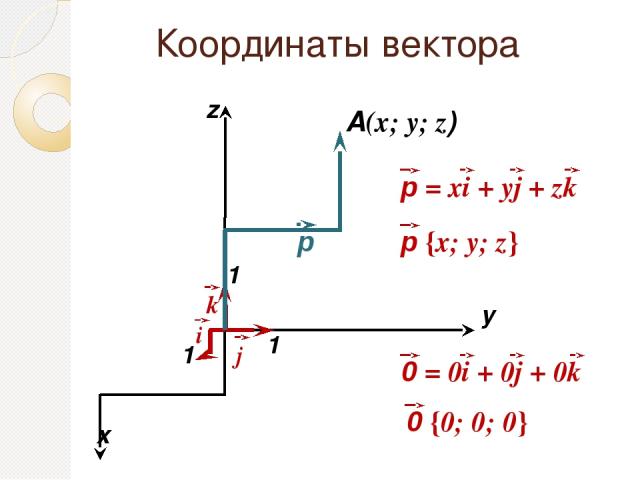
Координаты векторa x y A(x; y; z) 1 1 1 z р i р {х; у; z} 0 {0; 0; 0} k j

Действия над векторами Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. а {х1; у1; z1} b {х2; у2; z2}

Действия над векторами Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. а {х1; у1; z1} kа { kх1; kу1 ; kz1}

Примеры Дано: Найти: Решение: + + а {3; -7; 2} b {-5; 4; 1} 3а {9; -21; 6} -2b {10; -8; -2} р {19; -29; 4} -5а {-15; 35; -10} 6b {-30; 24; 6} q {-45; 59; -4}

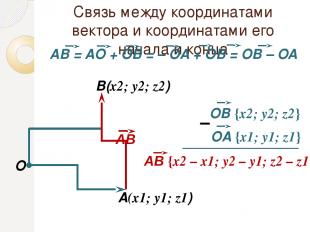
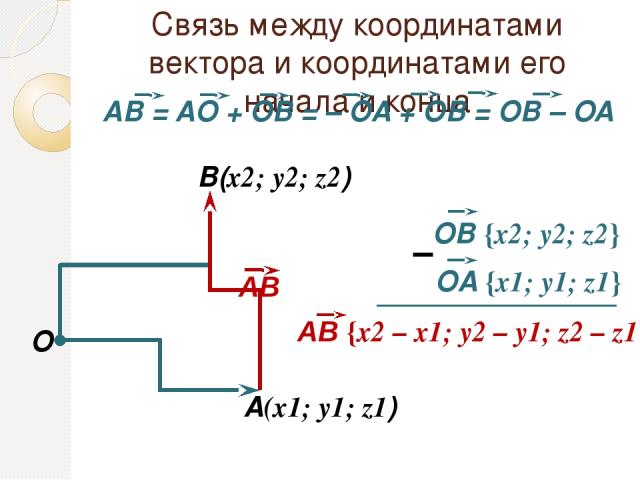
Связь между координатами вектора и координатами его начала и конца O A(x1; y1; z1) В(x2; y2; z2) – АВ АВ {х2 – x1; у2 – y1; z2 – z1} OВ {х2; у2; z2} OA {х1; у1; z1}

Связь между координатами вектора и координатами его начала и конца Каждая координата вектора равна разности соответствующих координат его конца и начала. Примеры А(5; 3; –4), В(–2; 4; 1) M(–3; 8; 2), N(0; –6; 5) АВ {–2 – 5; 4 – 3; 1–(–4)} АВ {–7; 1; 5} MN {0 – (–3); –6 – 8; 5 – 2} MN {3; –14; 3}

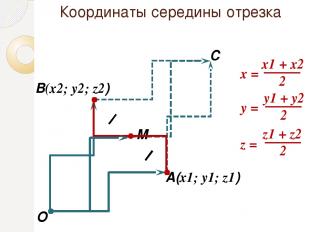
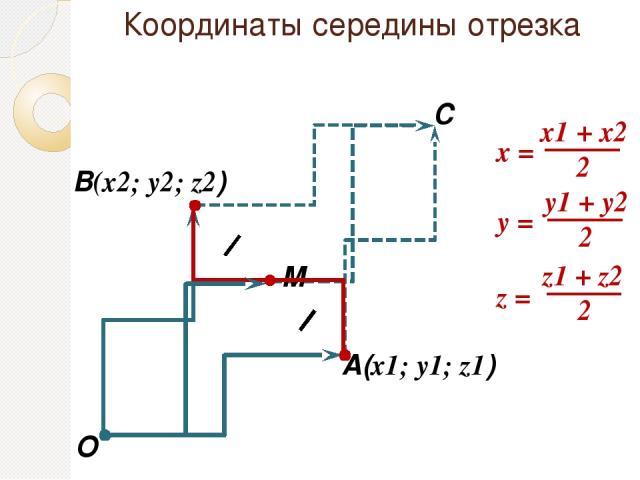
Координаты середины отрезка М A(x1; y1; z1) В(x2; y2; z2) С O x = y = z =

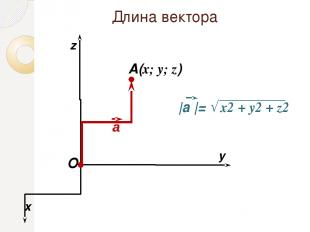
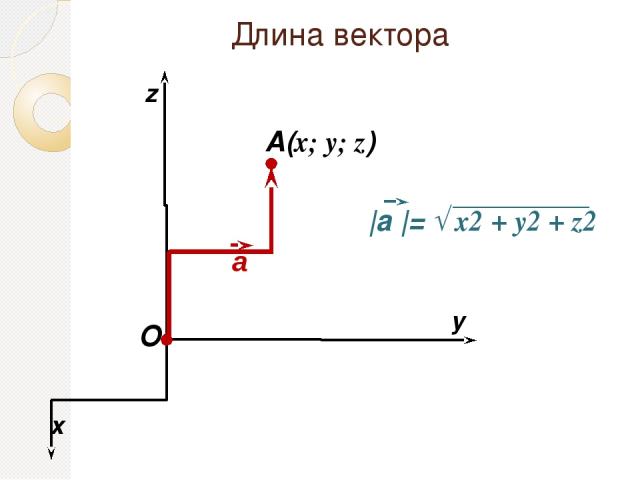
Длина вектора O x y A(x; y; z) z а

Расстояние между двумя точками A(x1; y1; z1) В(x2; y2; z2) АВ = √(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2

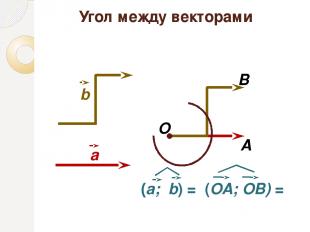
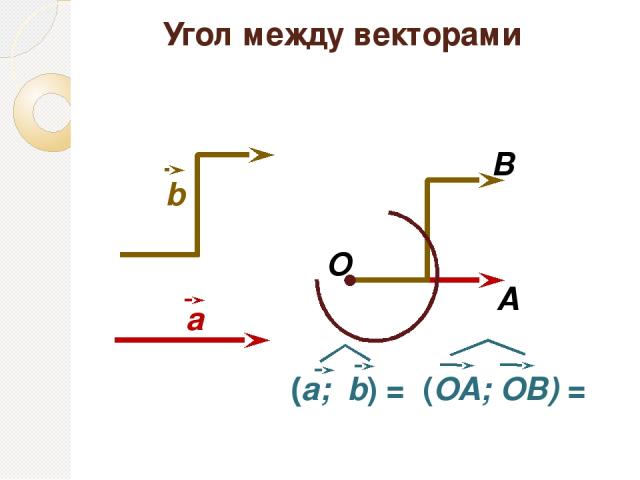
Угол между векторами О А В α a b (a; b) = (ОА; ОВ) = α

Скалярное произведение векторов Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними. Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны. a ∙ b = │a│∙│b│cos (a; b) a ∙ b = 0 a b

Скалярное произведение векторов Скалярный квадрат вектора (т.е. скалярное произведение вектора на себя) равен квадрату его длины. a ∙ a = a2 = |a|2 a b = x1x2 + y1 y2 + z1z2 Скалярное произведение векторов a{x1; y1; z1} и b{x2; y2; z2} выражается формулой

Скалярное произведение векторов x1x2 + y1 y2 + z1z2 cos α = Косинус угла α между ненулевыми векторами a {x1; y1; z1} и b {x2; y2; z2} вычисляется по формуле

Свойства скалярного произведения векторов a 2 ≥ 0, причем a 2 > 0 при а ≠ 0. Для любых векторов a, b, c и любого числа k справедливы равенства: a b = b a (переместительный закон). ( a + b ) c = a c + b c (распределительный закон). k ( a b ) = ( ka ) b (сочетательный закон).

Угол между прямыми │x1x2 + y1 y2 + z1z2│ cos φ = Пусть p {x1; y1; z1} и q {x2; y2; z2} – направляющие векторы прямых a и b. Косинус угла φ вычисляется по формуле: