Презентация на тему: Измерение длины


Познакомить учащихся с понятиями: длины окружности одним из вариантов измерения длины окружности числа


Попробуем измерить длину окружности Попробуем измерить длину окружности Построим окружность Выберем на ней несколько точек и соединим соседние точки отрезками. Получилась замкнутая ломаная, все узлы которой лежат на окружности. Такая ломаная называется вписанной в окружность


Если построенная ломаная не имеет самопересечений (пересечений звеньев), то длина ломаной приближает длину окружности Если построенная ломаная не имеет самопересечений (пересечений звеньев), то длина ломаной приближает длину окружности При этом, если узлы распределены по окружности неравномерно, то приближение плохое. Можно найти такое расположение точек, при котором длина ломаной будет равна трем радиусам Если же точки распределить равномерно, то ломаная будет приближать окружность гораздо лучше!

Расположите 6 точек на окружности так, чтобы длина ломаной равнялась 6. Как бы Вы ни старались, увеличить длину ломаной не удастся! Расположите 6 точек на окружности так, чтобы длина ломаной равнялась 6. Как бы Вы ни старались, увеличить длину ломаной не удастся! Наибольшая длина вписанной в окружность шестизвенной ломаной без самопересечений равна шести радиусам.
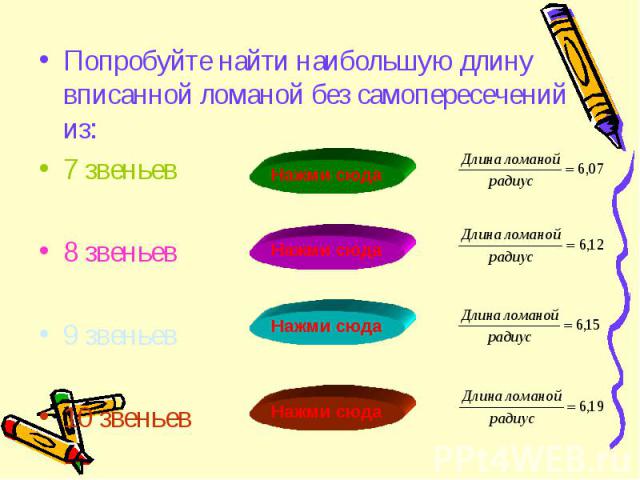
Попробуйте найти наибольшую длину вписанной ломаной без самопересечений из: Попробуйте найти наибольшую длину вписанной ломаной без самопересечений из: 7 звеньев 8 звеньев 9 звеньев 10 звеньев

Обратите внимание, что, дойдя до числа 6,28 радиусов, длина вписанной ломаной перестает возрастать!!! Обратите внимание, что, дойдя до числа 6,28 радиусов, длина вписанной ломаной перестает возрастать!!! Это свидетельствует о том, что мы нашли ломаные, длины которых совпадают с длиной окружности в трех первых (значащих) цифрах. Итак, мы нашли с некоторой точностью длину окружности. Она оказалась равна 6,28 · R (то есть 6,28 радиусов). Если длину окружности требуется измерить в тех же единицах, что и радиус, нужно умножить 6,28 на длину радиуса Эту формулу можно переписать по другому где D – длина диаметра окружности.

В наших экспериментах мы обнаружили удивительную закономерность: в единицах радиуса или диаметра любая окружность задается одним числом. В наших экспериментах мы обнаружили удивительную закономерность: в единицах радиуса или диаметра любая окружность задается одним числом. Такое независящее от вида фигуры число называется ее инвариантом. Число 3,14… является инвариантом окружности. Его принято обозначать и называть числом (“пи”) = 3,14…


Из древнеегипетских и вавилонских источников известно, что потребности того времени вполне удовлетворяло число, равное трем. Позже римляне принимали равное 3,12. Из древнеегипетских и вавилонских источников известно, что потребности того времени вполне удовлетворяло число, равное трем. Позже римляне принимали равное 3,12. В Древнем Египте считали равным 256/81=3,1604… В истории математики известно, что первое вычисление на основе строгих теоретических рассуждений было выполнено выдающимся математиком древности Архимедом. Архимед (ок.287-212 г.г. до н.э.) жил в г. Сиракузы на о. Сицилия. Погиб от рук римского воина. Перед гибелью Архимед сказал воину: «Не тронь мои круги!». В своем труде «Об измерении круга» он доказал, что находится между числами и , т.е. 3,1408 < <3,1429. Идеи Архимеда почти на два тысячелетия опередили свое время. Значение числа , вычисленное им, многие годы удовлетворяло практическим расчетам людей.

Вычислением числа занимались в более поздние века многие знаменитые математики. Вычислением числа занимались в более поздние века многие знаменитые математики. Французский математик Франсуа Виет вычислил в 1579 году с 9 знаками. Голландский математик Лудольф Ван Цейлен в 1596 г. публикует результат своего десятилетнего труда – число , вычисленное с 32 знаками. Леонард Эйлер (1707-1783) – ученый необычайной широты интересов и творческой продуктивности, автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки. Именно он в 1736 г ввел число для отношения длины окружности к длине ее диаметра. Постепенно увеличивая точность значений, в течение XVIII-XX веков нашли его значение с огромной точностью до 808 десятичных знаков.

Теперь известно, что число иррациональное, может быть представлено в виде бесконечной непериодической десятичной дроби. Приблизительное значение 3,14159265358979323846264… Теперь известно, что число иррациональное, может быть представлено в виде бесконечной непериодической десятичной дроби. Приблизительное значение 3,14159265358979323846264… С помощью компьютера число вычислено с точностью до миллиона знаков, но это представляет скорее технический, чем научный интерес…

ВЫВОДЫ: ВЫВОДЫ: Длина окружности равна 6,28 · R (то есть 6,28 радиусов) или где D - диаметр окружности

Данный урок составлен по материалу п. 24 «Длина окружности и площадь круга» учебника математики для 6 класса авторов Виленкина Н.Я., Жохова В.И., Чеснокова А.С., Шварцбурда С.И., М., “Мнемозина”, 2002 использует построения, выполненные в программе “Живая геометрия”. Данный урок составлен по материалу п. 24 «Длина окружности и площадь круга» учебника математики для 6 класса авторов Виленкина Н.Я., Жохова В.И., Чеснокова А.С., Шварцбурда С.И., М., “Мнемозина”, 2002 использует построения, выполненные в программе “Живая геометрия”.