Презентация на тему: Исследование жизненных ситуаций с помощью классического определения вероятности и решение простейших задач

Исследование жизненных ситуаций с помощью классического определения вероятностии решение простейших задачРазработала учитель математики СОШ № 74г КраснодараЗабашта Елена Георгиевна

Цель – научить учащихся вычислять вероятности в задачах, описывающих жизненные ситуацииЗадачи : знакомство с языком теории вероятностей; рассмотрение трех видов событий, классическое определение вероятности, знакомство с формулами условной вероятности, полной вероятности и формулой Бейеса и их применение при решении задач.

Виды наблюдаемых событийСлучайным событием называется такое событие, которое при осуществлении совокупности условий может либо произойти, либо не произойти.Достоверным событием называется событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий.Невозможным событием называют событие, которое заведомо не произойдет, если будет осуществлена совокупность условий.

Необходимые определенияЭлементарные события –неразложимые исходы опыта, причем единственно возможные.Объединением событий А и В называется событие С, состоящее в наступлении по крайней мере одного из событий А и В.Пересечением событий А и В называется событие С, состоящее в одновременном исполнении и А, и В.Два события А и В, пересечение которых – невозможное событие, называются несовместными событиями.Два события А и В называются совместными, когда существует по крайней мере одно элементарное событие, благоприятствующее и событию А, и событию В.Если объединение событий А и В – достоверное событие, а пересечение – невозможное событие, то события А и В называются противоположными.

Язык теории вероятностейΩ - пространство элементарных событийω - элементарное событиеА ⊂ В - А - событиеA∩В - пересечение или произведение событийА ⊂ В - событие А влечет событие ВАUВ - объединение или сумма событийĀ - противоположное событиеА\В - разность событийØ- невозможное событиеА∩В = Ø- события А и В несовместныА=В - события равносильны

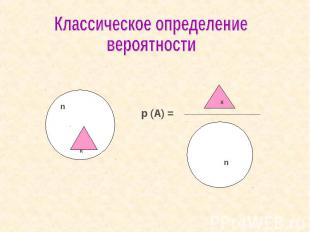
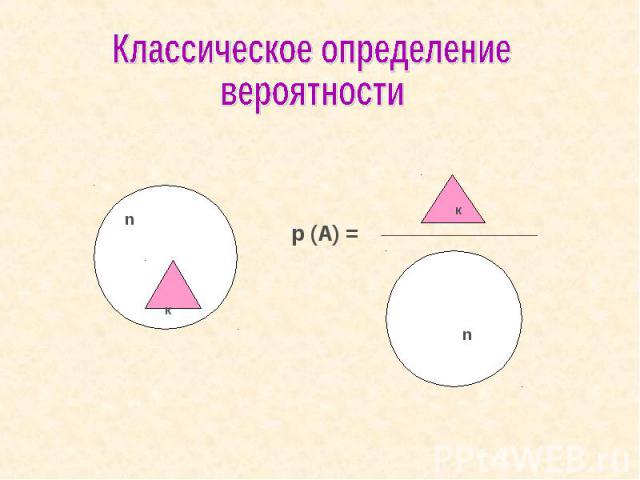
Классическое определениевероятности

Вероятность совместных и попарно несовместных событийВероятность объединения попарно несовместных событий равна сумме вероятностей этих событий. р (А U В) = р (А) + р (В). Вероятность объединения двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного осуществления. р (А U В) = р(А) + р (В) – р (А ∩ В).

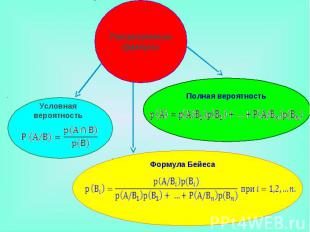
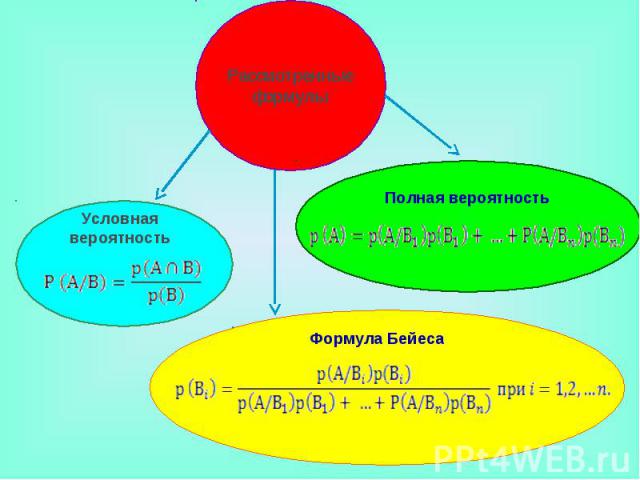
Рассмотренные формулы

Задача № 1Вычислить вероятность события А-«при бросании двух костей выпало 8 очков».

Решение.При бросании двух костей могут получиться следующие равновероятные результаты Как видно, всего возможных вариантов 36. Специально выделяются те случаи, когда произошло событие А. Таких случаев 5 - все они равновероятны. Следуя классическому определению вероятности, имеем: р(А) =

Задача № 2 Какова была вероятность того, что Сочи станет столицей Олимпиады - 2014?

Задача № 3.В лотерее выпущено 10000 билетов и установлено: 10 выигрышей по 200 р., 100 – по 100р., 500 – по 25 р. и 1000 выигрышей по 5 р. Гражданин купил один билет. Какова вероятность того, что он выиграет не меньше 25 рублей?

Решение. Обозначим события:А- «выигрыш не менее 25р.»,В-«выигрыш равен 25р.»,С -«выигрыш равен 100р.»,D- выигрыш равен 200р.».Поскольку куплен только один билет, то А = В U С U D, где события B, C, D попарно несовместны, поэтомур (А) = р(В U С U D) = р (B) + р (C) + р (D). р (B) = 0, 05, р (C)= 0,01, р (D)= 0, 001. р (А) = 0,05 + 0,01 + 0,001 = 0, 061. Ответ : р(А) = 0,061.

Задача № 4В ящике а белых и в черных шаров. Последовательно вынимаем два шара. Какова вероятность того, что они оба белые?

Решение. Обозначим события: А – «первый шар белый», В – « второй шар белый». Нам надлежит найти

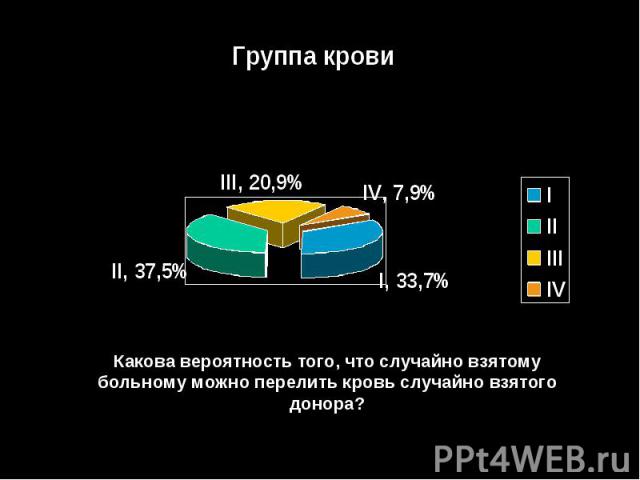
Задача № 5. При переливании группы крови надо учитывать группы крови донора и больного. Человеку, имеющему 4-ую группу крови, можно перелить кровь любой другой группы; человеку со 2 и 3 группой крови можно перелить кровь либо той же группы, либо 1-ой; человеку с 1-ой группой крови можно перелить только кровь 1-ой группы. Группы крови доноров представлены следующей диаграммой:

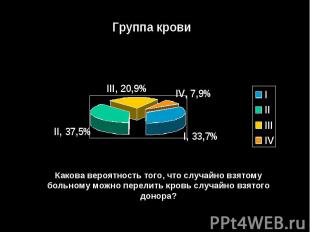
Какова вероятность того, что случайно взятому больному можно перелить кровь случайно взятого донора?

Решение. Обозначим события:С – «перелить кровь можно»,Аi- «ученик имеет i– ю группу крови»,Вi - «больной имеет i– ю группу крови».р (С/В₁) = 0,337,р(С/В₂ ) = 0,337 + 0,375,р(C/В₃) = 0,337+0,209 = 0,546,р(С/В₄) = 1.Значит, р(С) = р(В₁)р (С/В₁) + р(В₂)р(С/В₂)+ р(В₃) р(C/В₃)+ р(В₄) р(С/В₄)= 0, 573683. Ответ: р(С) = 0, 573683.

Математика – наука не из легких.Трудный и тернистый этот путь.Теоремы, леммы, аксиомы…Но с дороги этой не свернуть!Колмогоров, Чебышев и Гаусс,Лобачевский, Марков, Ляпунов…Столь великим, может, и не стать всем,Но науке посвятить я жизнь готов!

СПАСИБО ЗА ВНИМАНИЕ!