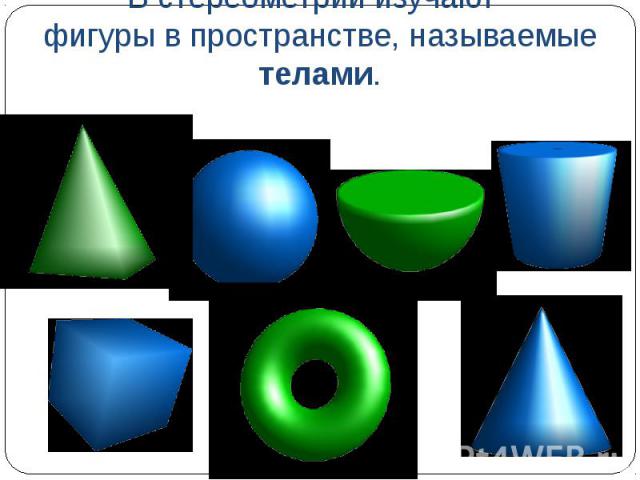
Презентация на тему: Геометрические фигуры в пространстве


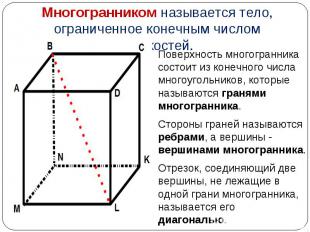
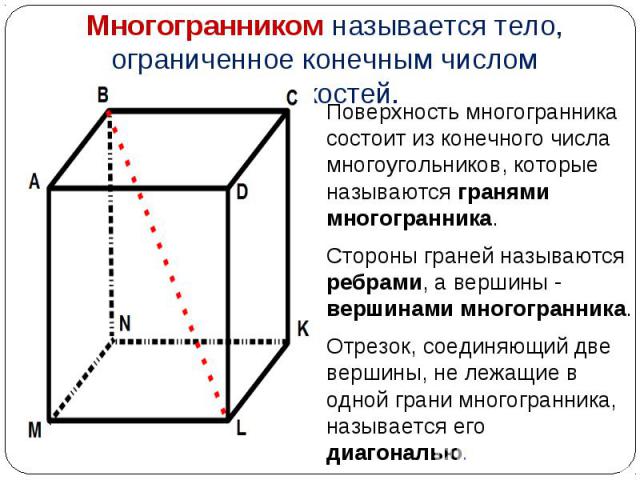
Поверхность многогранника состоит из конечного числа многоугольников, которые называются гранями многогранника. Поверхность многогранника состоит из конечного числа многоугольников, которые называются гранями многогранника. Стороны граней называются ребрами, а вершины - вершинами многогранника. Отрезок, соединяющий две вершины, не лежащие в одной грани многогранника, называется его диагональю.
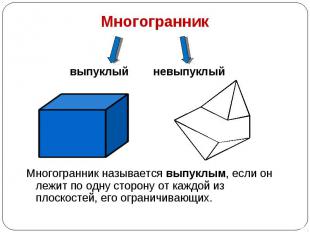
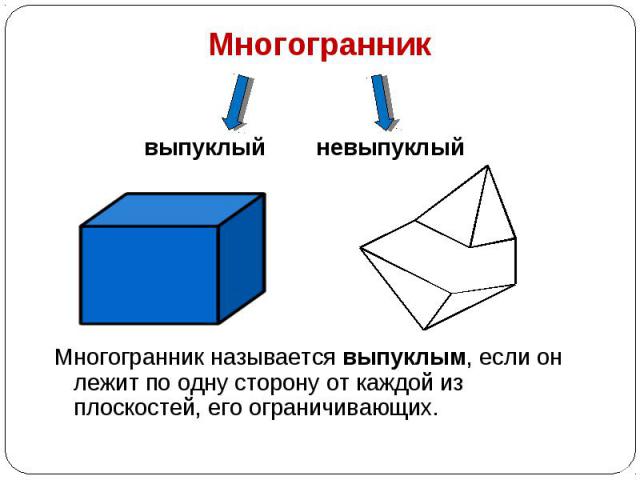
выпуклый невыпуклый Многогранник называется выпуклым, если он лежит по одну сторону от каждой из плоскостей, его ограничивающих.
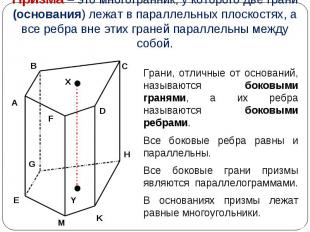
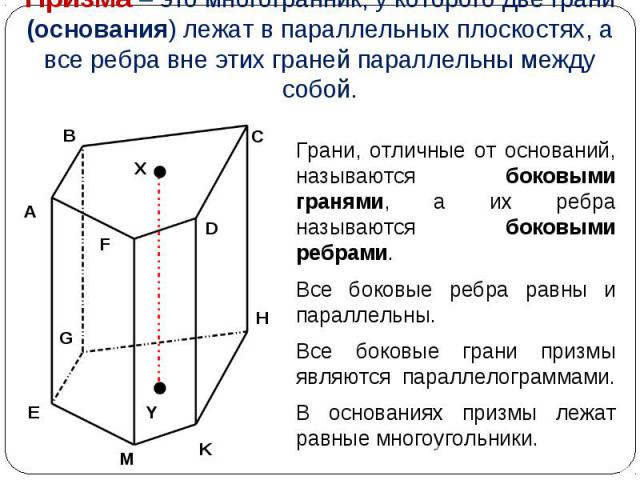
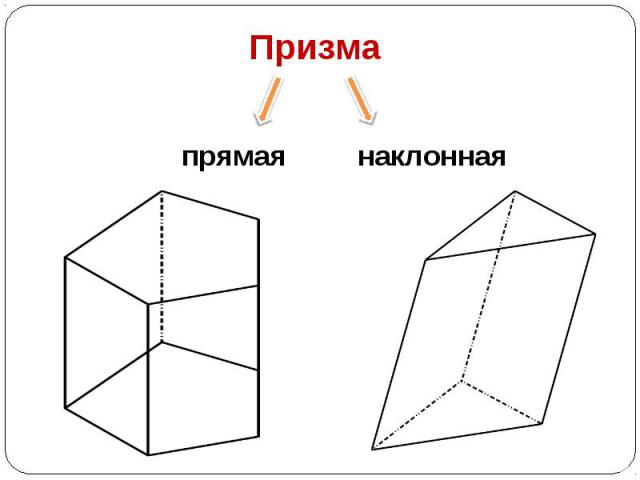
Грани, отличные от оснований, называются боковыми гранями, а их ребра называются боковыми ребрами. Грани, отличные от оснований, называются боковыми гранями, а их ребра называются боковыми ребрами. Все боковые ребра равны и параллельны. Все боковые грани призмы являются параллелограммами. В основаниях призмы лежат равные многоугольники.
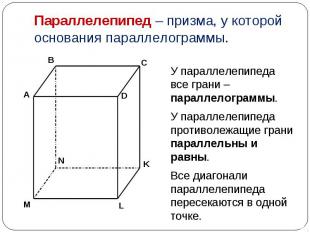
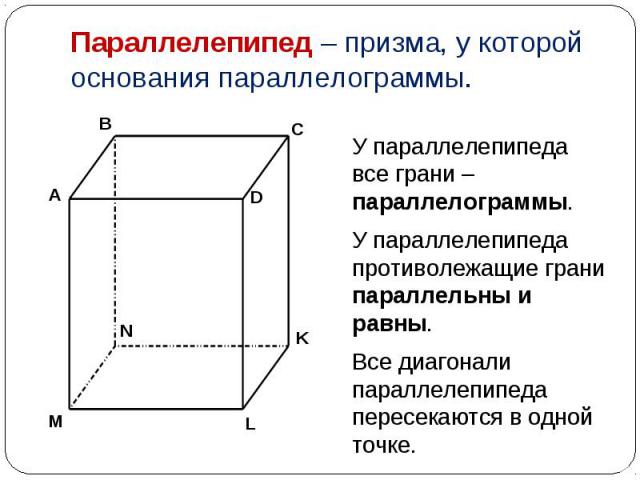
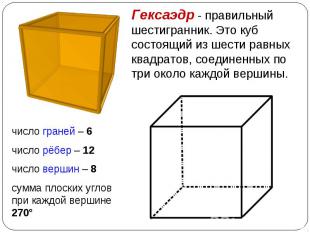
У параллелепипеда все грани –параллелограммы. У параллелепипеда все грани –параллелограммы. У параллелепипеда противолежащие грани параллельны и равны. Все диагонали параллелепипеда пересекаются в одной точке.
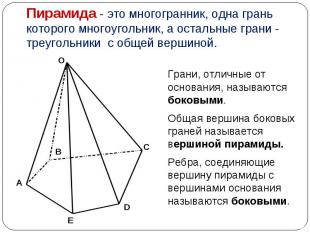
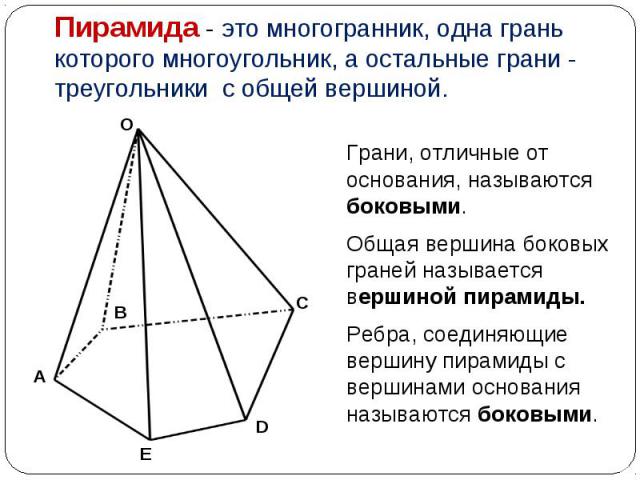
Грани, отличные от основания, называются боковыми. Грани, отличные от основания, называются боковыми. Общая вершина боковых граней называется вершиной пирамиды. Ребра, соединяющие вершину пирамиды с вершинами основания называются боковыми.

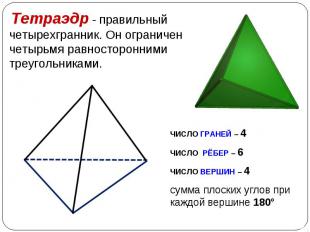
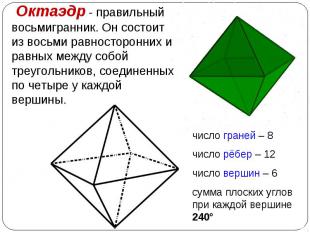



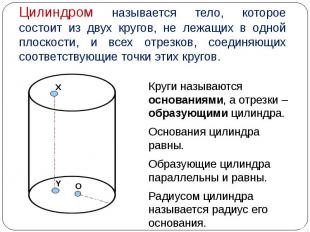
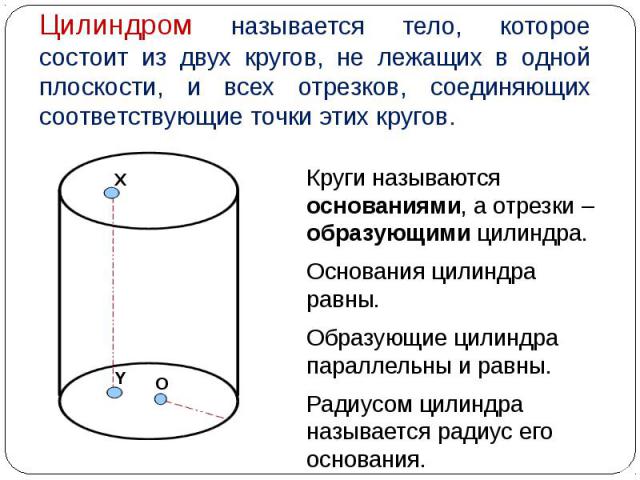
Круги называются основаниями, а отрезки – образующими цилиндра. Круги называются основаниями, а отрезки – образующими цилиндра. Основания цилиндра равны. Образующие цилиндра параллельны и равны. Радиусом цилиндра называется радиус его основания.
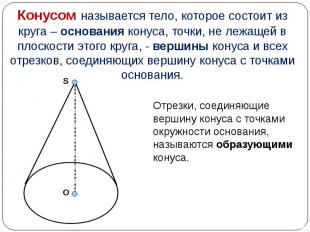
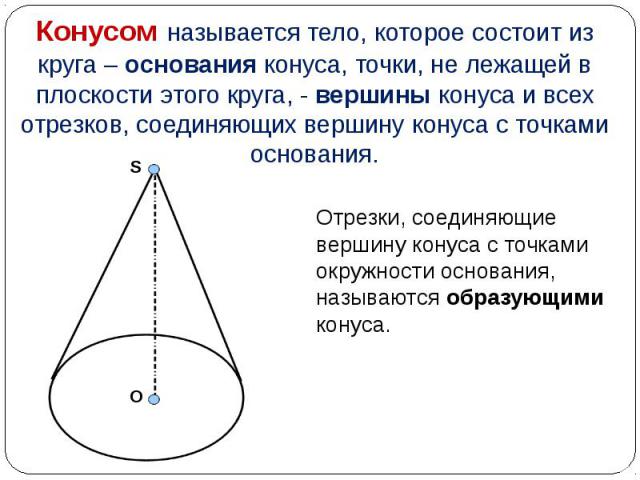
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.
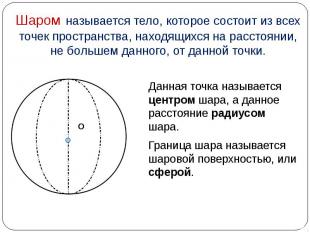
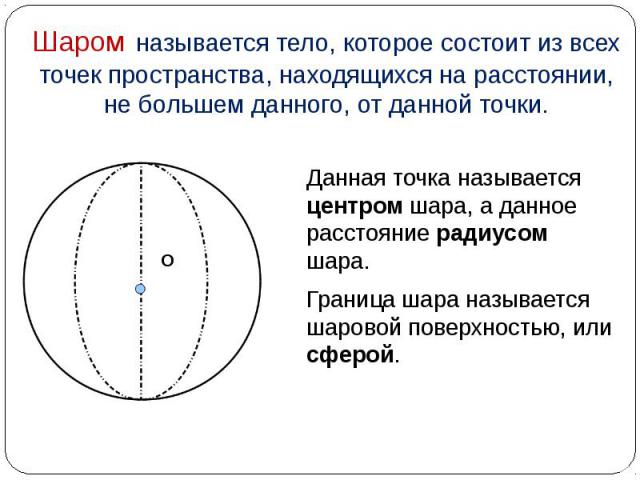
Данная точка называется центром шара, а данное расстояние радиусом шара. Данная точка называется центром шара, а данное расстояние радиусом шара. Граница шара называется шаровой поверхностью, или сферой.