Презентация на тему: Системы счисления

Системы счисления ИНФОРМАТИКА, 8 КЛАСС

СОДЕРЖАНИЕ Краткие сведения о системах счисления. Унарная система счисления. Непозиционные системы счисления. Позиционные системы счисления. Десятичная система. Двоичная система счисления. Двоичная арифметика. Восьмеричная система счисления. Шестнадцатеричная система счисления. Опорный конспект. Тест.

Системы счисления Система счисления – набор правил записи чисел, а также выполнения операций с ними. Цифры – знаки, при помощи которых записывается число. Алфавит – совокупность (множество) всех цифр системы счисления.

Унарная система счисления используется только один знак (чаще всего – “|”, но могут быть и другие); этот знак обозначает единицу в нашем обычном понимании

Непозиционные системы счисления Система является непозиционной, если количественное значение («вклад») цифры в числе не зависит от её положения в записи числа.

Непозиционные системы счисления унарная; египетская; шумерская; римская; славянская; и прочие…

Подробнее о римской системе счисления Правила: (обычно) не ставят больше трех одинаковых цифр подряд если младшая цифра (только одна!) стоит слева от старшей, она вычитается из суммы (частично непозиционная!) Примеры: MDCXLIV =

Позиционные системы счисления Система является позиционной, если количественное значение («вклад») цифры в числе зависит от её положения в записи числа.

Самое важное Разряды (i) нумеруем от нуля справа налево (для дробных чисел – нулевой разряд находится слева от запятой); Правила устного счёта на информатике: 1) начинаем от нуля; 2) доходим до максимальной цифры в системе счисления; 3) увеличиваем цифру в разряде слева на 1; 3а) если в разряде слева стоит максимальная цифра, то увеличиваем на 1 цифру в разряде ещё левее (повторяем пункт до первого разряда с не максимальной цифрой); 4) обнуляем все разряды справа от того, который мы увеличили на 1; 5) повторяем пункты 1-4 до нужного числа.

Узловые и алгоритмические числа

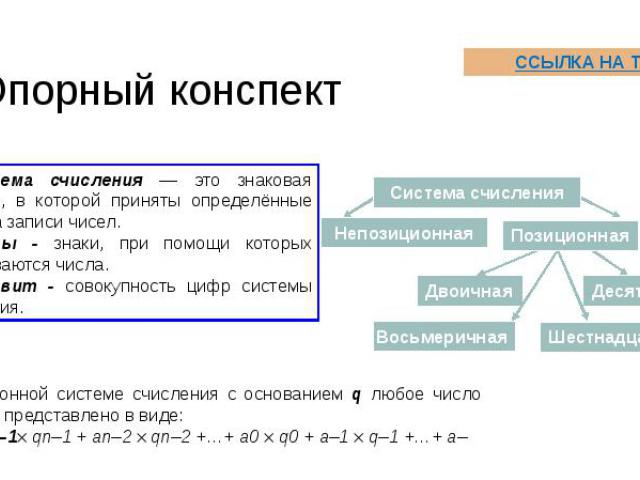
Расширенная форма В позиционной системе счисления с основанием q любое число может быть представлено в виде: Aq =±(an–1 qn+ an–2 qn-1+…+ a0 q0+ a–1 q–1+…+ a–m q–m) Здесь: А — число; q — основание системы счисления; ai — цифры, принадлежащие алфавиту данной системы счисления; n — количество целых разрядов числа - 1; m — количество дробных разрядов числа; qi — «вес» i-го разряда. Такая запись числа называется развёрнутой формой записи.

Расширенная форма СЛОЖНО? Примеры: 2345,6710 = 2*103 + 3*102 + 4*101 + 5*100 + 6*10-1 + 7*10-2 2345,678 = 2*83 + 3*82 + 4*81 + 5*80 + 6*8-1 + 7*8-2

Двоичная система счисления

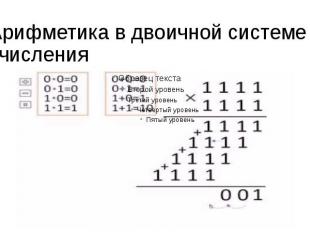
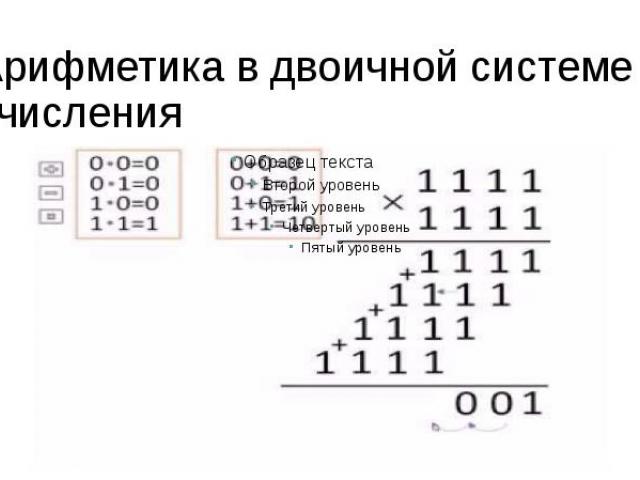
Арифметика в двоичной системе счисления

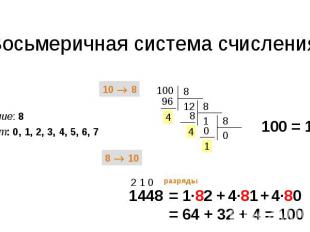
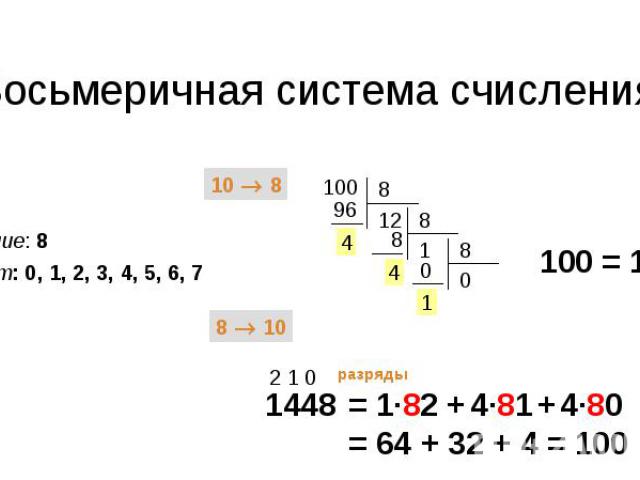
Восьмеричная система счисления

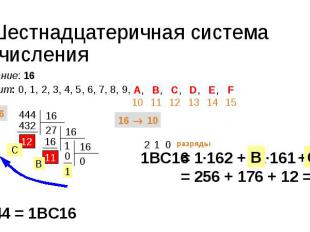
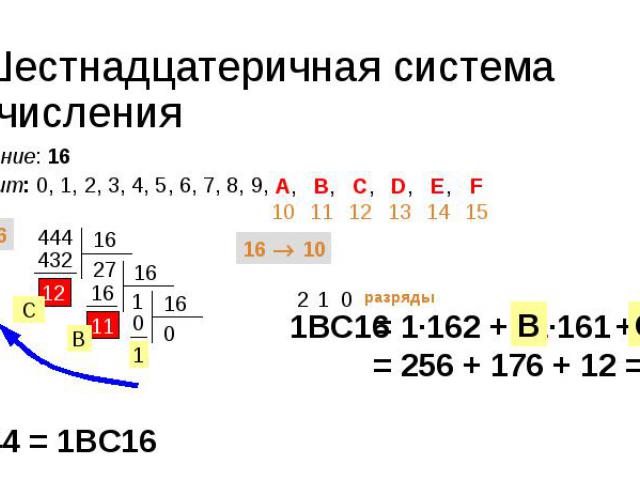
Шестнадцатеричная система счисления

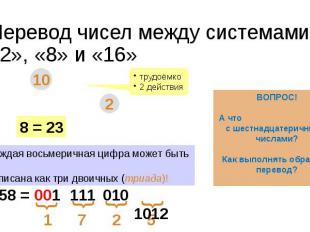
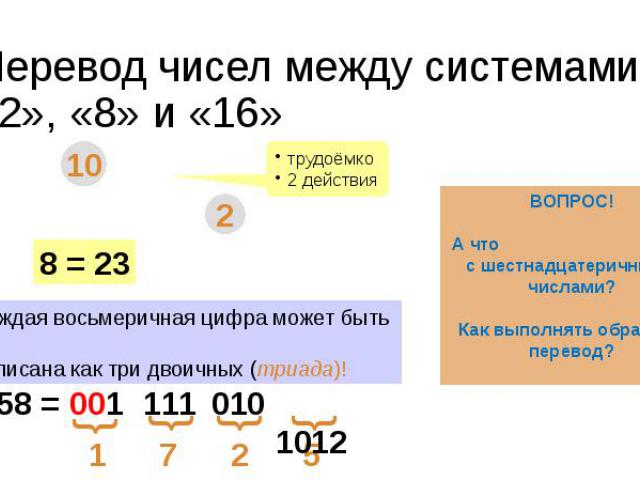
Перевод чисел между системами «2», «8» и «16»

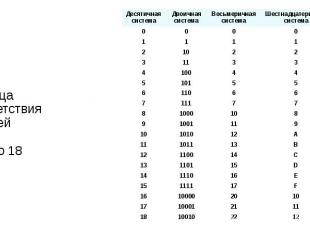
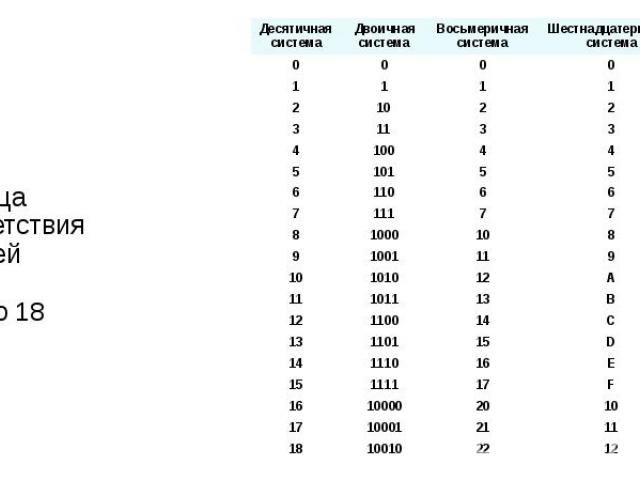
Таблица соответствия записей чисел от 0 до 18

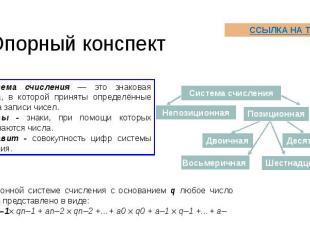
Опорный конспект