Презентация на тему: Представление информации в различных системах счисления

Представление информации в различных системах счисления

Для перевода двоичного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания двоичной системы счисления на соответствующие цифры в разрядах двоичного числа. Число представляется в виде суммы произведений ЦИФРЫ на ВЕС РАЗРЯДА. Вес разряда – это основание СС в степени равной номеру разряда. Разряды нумеруются от разряда единиц- влево. Разряд единиц имеет номер 0. 10112 = 1*23+ 0*22+ 1*21+ 1*20= 1*8+ 0*4+ 1*2+ 1*1= 1110 3 2 1 0 Разложение чисел по степеням основания

Системы счисления Система счисления - совокупность приемов и правил для изображения чисел с помощью символов (цифр), имеющих определенные количественные значения. Система счисления непозиционная позиционная

Непозиционная система счисления В непозиционных системах счисления вес цифры (то есть тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти. Унарная – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …)

Славянская система счисления алфавитная система счисления (непозиционная) Более совершенные непозиционные с/с. К их числу относились славянская, греческая, финикийская и др. В них числа от 1 до 9, целые количества десятков (от 10 до 90) и целые количества сотен (от 10 до 900) обозначались буквами алфавита. В России славянская нумерация сохранилась до конца 17 века. При Петре I возобладала арабская нумерация, которой пользуемся до сих пор. Греки над буквами, обозначающими числа, ставили специальный знак – титло.

Римская система счисления В ней для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используются заглавные латинские буквы I, V, X, L, С, D и М (соответственно), являющиеся «цифрами» этой системы счисления. Число в римской системе счисления обозначается набором стоящих подряд «цифр».

Римская система счисления Правила: (обычно) не ставят больше трех одинаковых цифр подряд если младшая цифра (только одна!) стоит слева от старшей, она вычитается из суммы (частично непозиционная!) Примеры: MDCXLIV = 1000 + 500 + 100 – 10 + 50 – 1 + 5 2389 = 2000 + 300 + 80 + 9 2389 = M M C C C L X X X I X M M CCC LXXX IX = 1644

Позиционная система счисления В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.     Например, в числе 357,6  первый символ  3 означает 3 сотни; второй символ 5 означает 5 десятков, третий символ  7 означает 7 единиц, а четвертый символ  6 означает 6 десятых долей единицы. Основание позиционной системы счисления - это количество различных символов, используемых для изображения чисел в данной системе счисления.     В настоящее время, кроме хорошо известной нам десятичной системы счисления, в вычислительной технике используются  двоичная, восьмеричная, и шестнадцатеричная системы счисления. Все применяемые в настоящее время системы счисления позиционные. 234 Две сотни Три десятка Четыре единицы

Двоичная СС В двоичной системе счисления для изображения чисел используется 2 символа: 0,  1. Поэтому основанием двоичной системы счисления является число 2. Например, число 5 в двоичной СС в полной форме записывается следующим образом: 5 = 1*22+0*21 +1*20 В сокращенной и более привычной форме число 5 в двоичной системе записывается так: 510 = 1012

Восьмеричная СС Приняв за основание число 8, получаем восьмеричную систему счисления: 0, 1, 2, 3, 4, 5, 6, 7 Всего 8 разных знаков составляют алфавит восьмеричной системы счисления Можно записать любое число включая все эти знаки : 237, 145, 32, 12765… - обратите внимание: используем цифры от 0 до 7 Для восьмеричной системы счисления q=8

Десятичная СС Приняв за основание число 10, получаем знакомую нам десятичную систему счисления: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Всего 10 разных знаков составляют алфавит десятичной системы счисления. Можно записать любое число включая все эти знаки: 237, 12840, 987, 23... Основание системы счисления обозначают буквой q. Для десятичной системы счисления q=10

Шеснадцатеричная СС Приняв за основание число 16, получаем шестнадцатеричную систему счисления. Здесь мы можем воспользоваться 10 знаками десятичной системы, добавив еще 6 знаков – буквы латинского алфавита (A, B, C, D, E, F): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E,F 10 11 12 13 14 15 Всего 16 разных знаков составляют алфавит шестнадцатеричной системы счисления. Можно записать любое число включая все эти знаки: А37, 1В45, F302, 1A3C5… - обратите внимание: используем знаки от 0 до F. Для шестнадцатеричной системы счисления q=16

"Алфавит" различных систем счисления Система счисления Основание Размерность алфавита Цифры Двоичная 2 2 0, 1 Восьмеричная 8 8 0,1,2,3,4,5,6,7 Десятичная 10 10 0,1,2,3,4,5,6,7,8,9 Шестнадцатеричная 16 16 0,1,2,3,4,5,6,7,8,9,А,В,С,D,T,F

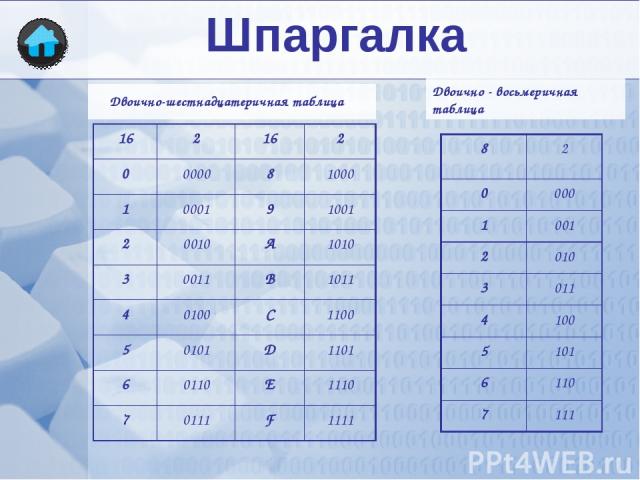
Двоично-шестнадцатеричная таблица Двоично - восьмеричная таблица Шпаргалка 16 2 16 2 0 0000 8 1000 1 0001 9 1001 2 0010 А 1010 3 0011 В 1011 4 0100 С 1100 5 0101 D 1101 6 0110 Е 1110 7 0111 F 1111 8 2 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111

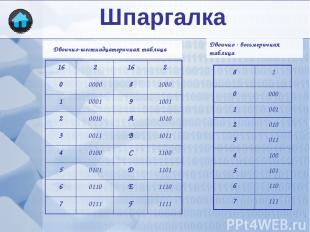
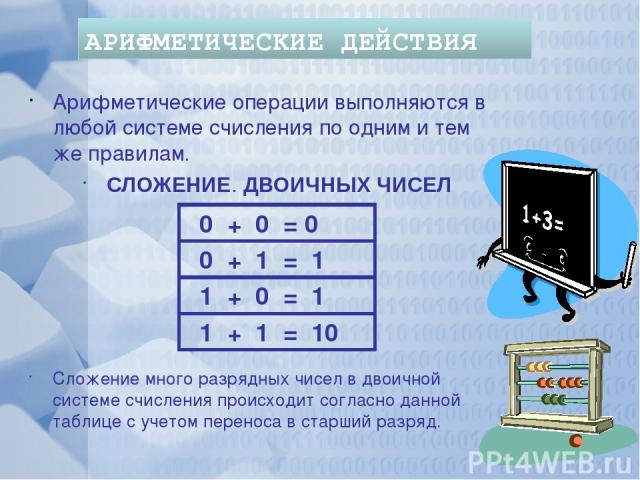
1112 1001012 + 112 + 10112 10102 1100002 СЛОЖЕНИЕ ДВОИЧНЫХ ЧИСЕЛ АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ 100112 + 1112 110102 1 102 + 112 2 1001 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10

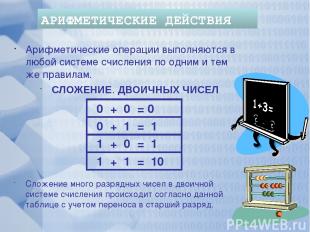
1102 1001012 + 1012 + 110112 СЛОЖЕНИЕ ДВОИЧНЫХ ЧИСЕЛ 100112 + 1012 1112 + 102 10012 Проверить Проверить Проверить Проверить 110002 10112 10000002 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1+ 1 = 11 1 + 1 = 10

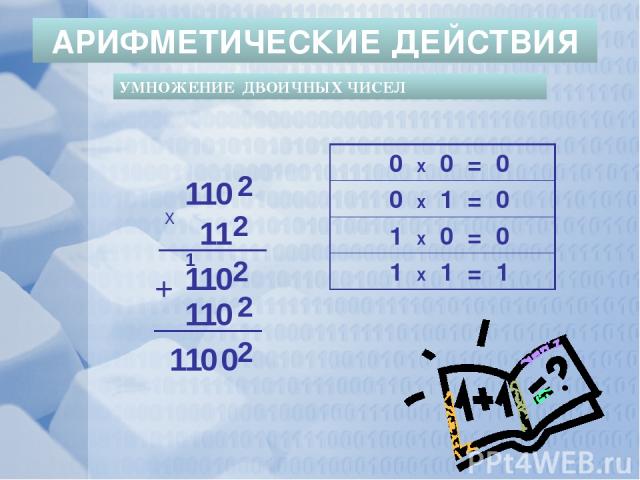
УМНОЖЕНИЕ ДВОИЧНЫХ ЧИСЕЛ АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ 1 0 1 1 1 1 1 1 1 0 0 0 0 1 Х + 1 1 2 2 2 2 2 0Х0 = 0 0Х1 = 0 1Х0 = 0 1Х1 = 1

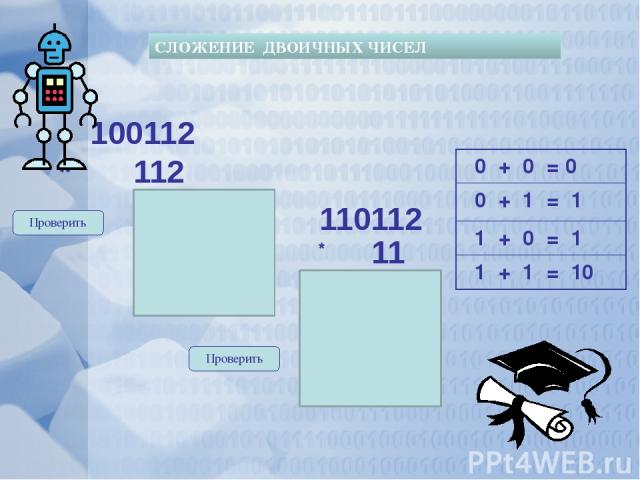
СЛОЖЕНИЕ ДВОИЧНЫХ ЧИСЕЛ 100112 * 112 Проверить Проверить 100112 1011102 100112 + 110112 110112 110112 112 101102 * + 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10

Разложение чисел по степеням основания Аналогично происходит перевод чисел из других систем счислений в десятичную. 24518 = 2 · 83 + 4 · 82 + 5 · 81 + 1 · 80 6758= ? Проверить 6*82+7*81+5*80= 6*64+7*8+5*1=44510 1А16= ? Проверить 1*161+10*160=16+10=2610

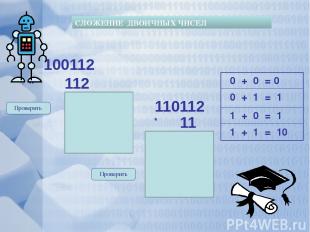
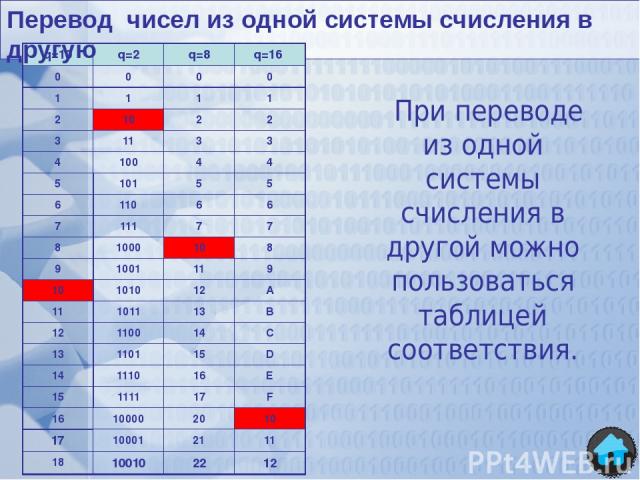
При переводе из одной системы счисления в другой можно пользоваться таблицей соответствия. Перевод чисел из одной системы счисления в другую q=10 q=2 q=8 q=16 0 0 0 0 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 17 10001 21 11 18 10010 22 12

Правила перевода Из десятичной системы счисления в позиционные системы счисления: Разделить десятичное число на основание системы счисления. Получится частное и остаток. Выполнять деление до тех пор, пока последнее частное не станет меньшим основания новой системы счисления. Записать последнее частное и все остатки в обратном порядке. Полученное число и будет записью в новой системы счисления.

Представим число 6210 в двоичной системе счисления: 31 0 15 7 3 1 Ответ: 6210 = 1111102 62 62 2 1 2 1 2 1 2 1

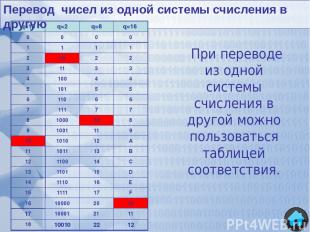
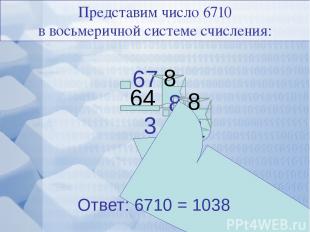
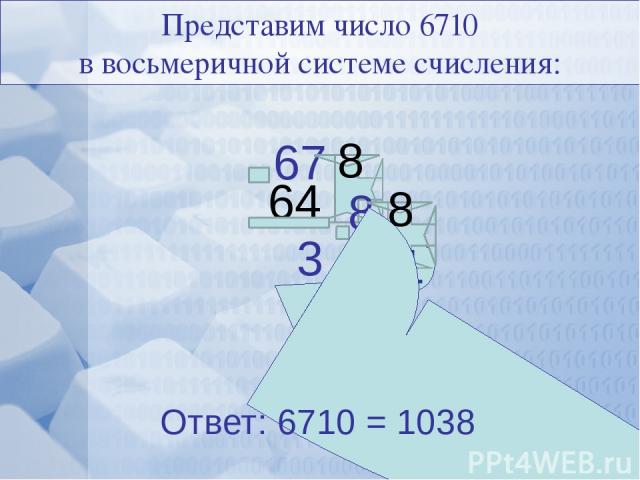
67 Представим число 6710 в восьмеричной системе счисления: 8 3 1 Ответ: 6710 = 1038 8 64 8 0

Представим число 9110 в шестнадцатеричной системе счисления: 91 5 Ответ: 9110 = 5B16 16 11

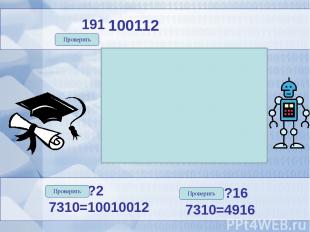
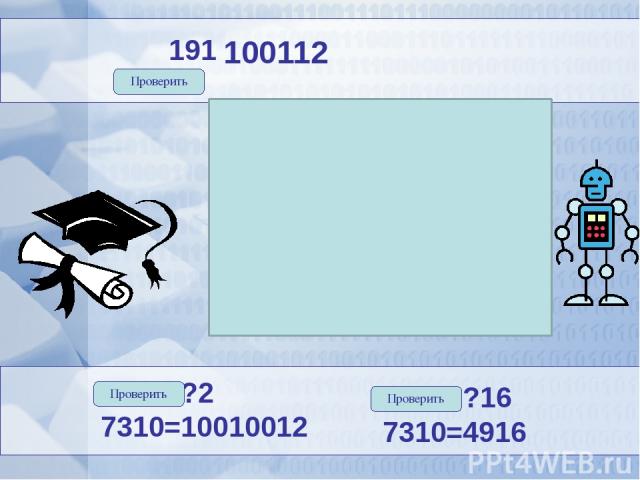
0 2 4 2 2 2 1 19 2 18 9 2 8 4 0 1 1 1910= Проверить 100112 7310=?2 7310=10010012 7310=?16 7310=4916 Проверить Проверить