Презентация на тему: кодирование информации

Представление чисел в памяти компьютера имеет специфическую особенность, связанную с тем, что в памяти компьютера они должны располагаться в байтах – минимальных по размеру адресуемых (т.е. к ним можно обращаться) ячейках памяти. Представление чисел в памяти компьютера имеет специфическую особенность, связанную с тем, что в памяти компьютера они должны располагаться в байтах – минимальных по размеру адресуемых (т.е. к ним можно обращаться) ячейках памяти.

Очевидно, адресом числа следует считать адрес первого байта. Очевидно, адресом числа следует считать адрес первого байта. В байте может содержаться произвольный код из 8 двоичных разрядов, и задача представления состоит в том, чтобы указать правила, как в одном или нескольких байтах записать число.

Числа могут быть: Числа могут быть: целые точные, дробные точные, рациональные, иррациональные, дробные приближенные, числа могут быть положительными и отрицательными. Числа могут быть «карликами», например масса атома, «гигантами», например, масса земли. Каждое из перечисленных множеств потребует для оптимального представления в памяти компьютера свое количество байтов.

Вопрос. Какие множества чисел принято выделять в математике? Вопрос. Какие множества чисел принято выделять в математике? Отличаются ли эти множества от названных выше множеств? Объясните причины этого.

Очевидно, единого оптимального представления для всех действительных чисел создать невозможно, Очевидно, единого оптимального представления для всех действительных чисел создать невозможно, поэтому создатели вычислительных машин пошли по пути разделения единого по сути множества чисел на типы (например, целые в диапазоне от.. до.., приближенные с плавающей точкой с количеством значащих цифр … и т.д.) Для каждого в отдельности типа создается собственный способ представления.

Вопрос. Как можно представить целые числа от 0-255 в двоичном коде? Вопрос. Как можно представить целые числа от 0-255 в двоичном коде? Сколько места они будут занимать?

Если нужны отрицательные числа, то знак числа может быть закодирован отдельным битом, обычно это старший бит (ноль – значит знак плюс, 1 – значит знак минус). Если нужны отрицательные числа, то знак числа может быть закодирован отдельным битом, обычно это старший бит (ноль – значит знак плюс, 1 – значит знак минус). В таком случае могут быть закодированы целые числа от -127 до 127. Этот способ называется прямым кодом.

Аналогично целые числа от 0 до 65535 и целые числа от -32768 до 32767 в двоичной системе счисления могут быть представлены в двухбайтовый ячейках. Аналогично целые числа от 0 до 65535 и целые числа от -32768 до 32767 в двоичной системе счисления могут быть представлены в двухбайтовый ячейках.

Действительные числа в математике представляются конечными или бесконечными дробями, т.е. точность представления чисел не ограничена. Действительные числа в математике представляются конечными или бесконечными дробями, т.е. точность представления чисел не ограничена. Вопрос. Можно ли представить действительное число в компьютере с произвольной неограниченной точностью?

В компьютерах числа хранятся в регистрах и ячейках памяти, которые представляют собой последовательность байтов с ограниченным количеством разрядов. В компьютерах числа хранятся в регистрах и ячейках памяти, которые представляют собой последовательность байтов с ограниченным количеством разрядов.

Следовательно, бесконечные или очень длинные числа усекаются до некоторой длины и в компьютерном представлении выступают как приближенные. Следовательно, бесконечные или очень длинные числа усекаются до некоторой длины и в компьютерном представлении выступают как приближенные. В большинстве систем программирования в написании действительных чисел целая и дробная часть отделяется точкой, а не запятой.

Для представления действительных чисел, как очень маленьких, так и очень больших, удобно использовать форму записи чисел в виде произведения: Для представления действительных чисел, как очень маленьких, так и очень больших, удобно использовать форму записи чисел в виде произведения: где m – мантисса числа; q – основание системы счисления; p – целое число, называемое порядком Такая запись числа называется представлением числа с плавающей точкой.

Например число 1234,56 можно представить в одном из видов Например число 1234,56 можно представить в одном из видов Очевидно, что представление неоднозначно.

Для однозначного представления числа используют нормализованную форму записи, при которой выполняется следующее условие Для однозначного представления числа используют нормализованную форму записи, при которой выполняется следующее условие (для десятичной системы счисления ).

Действительные числа в компьютерах различных типов записываются по-разному, тем не менее, существуют несколько международных стандартов, различающихся по точности, но имеющих одинаковую структуру. Действительные числа в компьютерах различных типов записываются по-разному, тем не менее, существуют несколько международных стандартов, различающихся по точности, но имеющих одинаковую структуру.

Первый разряд представления используется для записи знака мантиссы. Первый разряд представления используется для записи знака мантиссы. За ним следует группа разрядов, определяющих порядок, а остальные разряды определяют абсолютную величину мантиссы. Размеры обеих групп разрядов фиксируются. Поскольку порядок может быть как положительным так и отрицательным, то нужно решить проблему его знака.

Вместо истинного значения порядка (например, отрицательного числа) хранится число называемое его характеристикой (или смещенным порядком). Вместо истинного значения порядка (например, отрицательного числа) хранится число называемое его характеристикой (или смещенным порядком). Для получения характеристики необходимо к порядку к прибавить смещение. Так, для хранения порядка 8 бит и значений от -128 до 127 используется смещение 128. тогда для представления порядка будут использоваться значения от 0 до 255.

Чем больше разрядов отводится для записи мантиссы, тем больше точность числа. Чем больше разрядов отводится для записи мантиссы, тем больше точность числа.

Как уже говорилось, минимальной адресуемой единицей памяти является байт, но представление числа требует большего объема. Как уже говорилось, минимальной адресуемой единицей памяти является байт, но представление числа требует большего объема. Если число занимает группу байт, то адресом числа будет адрес первого байта группы. Однако произвольно взятый из памяти байт нечего нам не скажет о том, частью какого информационного объекта он является – целого числа, числа с плавающей точкой и т.д.

Таким образом, можно сделать вывод, что кроме представления данных в двоичном коде, параллельно решается обратная задача – задача интерпретации кодов, т.е. как из кодов восстановить первоначальные данные. Таким образом, можно сделать вывод, что кроме представления данных в двоичном коде, параллельно решается обратная задача – задача интерпретации кодов, т.е. как из кодов восстановить первоначальные данные. Для представления основных видов информации (числа целые, числа с плавающей точкой, символы, звук и т.д.) в системах программирования используют специального вида абстракции – типы данных. Каждый тип данных определяет логическую структуру представления и интерпретации для соответствующих данных.

Тексты являются важнейшим источником информации. Тексты являются важнейшим источником информации. Именно такой характер имеют экономические, плановые, учебные данные, представленные на естественном или искусственном языке. Каждый язык использует свою знаковую систему, основанную на алфавите. Письменность можно рассматривать как метод представления на материальных носителях знаков звуковой системы разговорного языка.

В настоящее время известно множество средств, позволяющих разнообразить письменные документы: В настоящее время известно множество средств, позволяющих разнообразить письменные документы: шрифты, абзацы, заголовки, для создания четкой структуры документов используются главы, параграфы… Как кодируются символы, элементы текстов, текстовые документы?

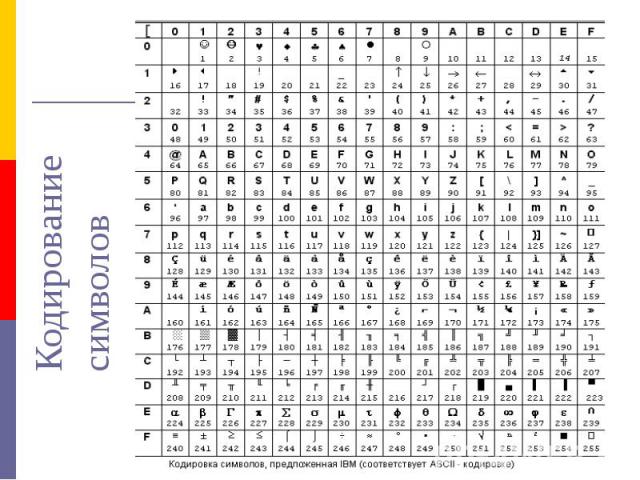
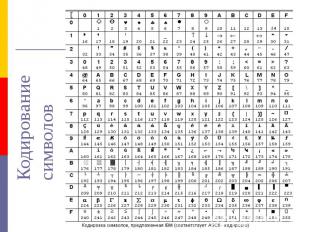
Символы. Символы. Двоичное кодирование символьных данных производиться заданием кодовых таблиц, согласно которым каждому символу ставится в соответствие одно- или двухбайтовый код. Помимо этого, кодовая таблица ставит в соответствие кодам клавиши на клавиатуре и начертание символа на экране монитора.

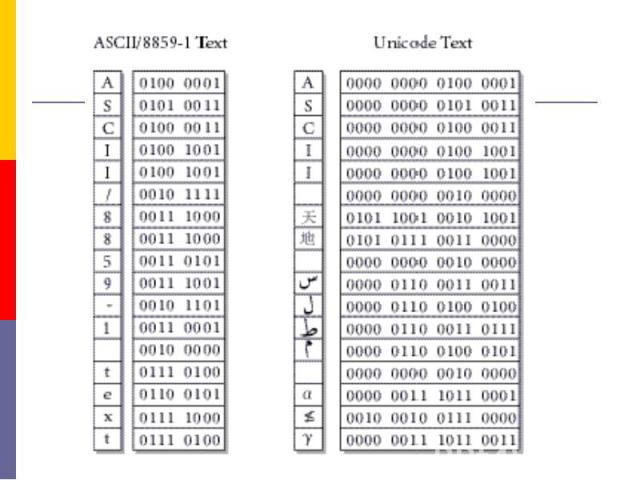
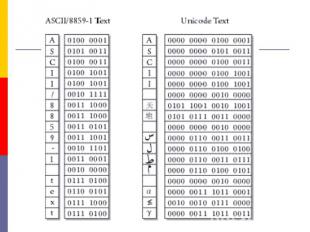
В 1991 г. производители программных продуктов и стандартизаторы пришли к соглашению о выработке единого стандарта ISO 10646-1 (он же Unicode 3.0). В 1991 г. производители программных продуктов и стандартизаторы пришли к соглашению о выработке единого стандарта ISO 10646-1 (он же Unicode 3.0). Код построен по 31-битной схеме, но использует только 2 байта для кодировании одного символа. Два байта (16 бит) создают кодов, которые описывают цифры, буквы латинского алфавита и многих других национальных алфавитов, спецсимволы, знаки арифметических действий и т.д. все текстовые документы в этой кодировке вдвое длиннее, что сначала задерживало ее внедрение, но современный уровень технических средств допускает такую возможность. (MS Word, начиная с версии 8.0) использует шрифты Unicode 3.0

Текстовые строки. Текстовая (символьная строка) – это конечная последовательность символов. Текстовые строки. Текстовая (символьная строка) – это конечная последовательность символов. Это может быть осмысленный текст или произвольный набор, короткое слово или целая книга. Длина символьной строки – это количество символов в ней. Записывается в память символьная строка двумя способами: либо число, обозначающее длину текста, затем текст; либо текст, а затем разделитель строк.

Текстовые документы используются для хранения и обмена данными в информационных системах, но сплошной, не разбитый на логические фрагменты текст воспринимается тяжело. Текстовые документы используются для хранения и обмена данными в информационных системах, но сплошной, не разбитый на логические фрагменты текст воспринимается тяжело.

Структурирование текста достигается форматированием – специфическим расположением текста при подготовке его к печати. Структурирование текста достигается форматированием – специфическим расположением текста при подготовке его к печати. Для анализа структуры текста были разработаны языки разметки, которые текстовые метки (маркеры, теги) используемые для обозначения частей документа, записывают вместе с основным текстом в текстовой форме. Программы, анализирующие текст, структурируют его, считывая теги.

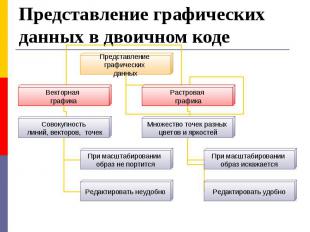
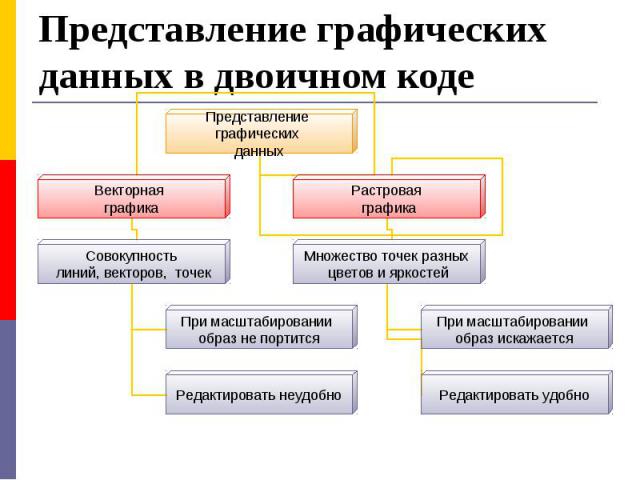
Векторные изображения состоят из отрезков линий (векторов). Они легко масштабируются без потери качество изображения. При помощи средств векторной графики удобно создавать чертежи и рисунки. Векторные изображения состоят из отрезков линий (векторов). Они легко масштабируются без потери качество изображения. При помощи средств векторной графики удобно создавать чертежи и рисунки. Растровые изображения состоят из мозаики цветных квадратиков. Они не поддаются масштабированию. Но с их помощью удобно отображать сложные реалистичные картины и фотографии.

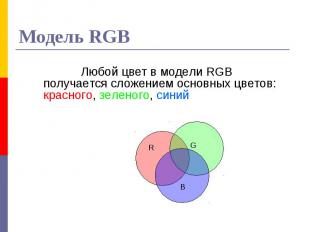
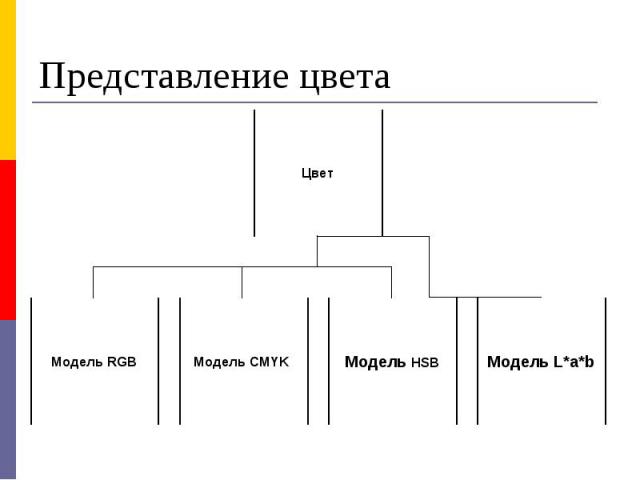
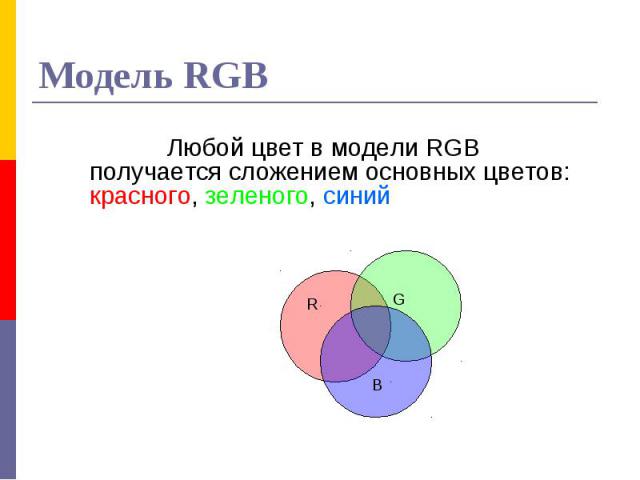
Закон трехмерности – любой цвет может быть представлен композицией 3 основных цветов (красный, зеленый, синий в данной модели) Закон трехмерности – любой цвет может быть представлен композицией 3 основных цветов (красный, зеленый, синий в данной модели) Закон непрерывности – к любому цвету можно подобрать бесконечно близкий; Закон аддитивности – цвет смеси зависит только от цвета составляющих;

Каждый составляющий цвет характеризуется своей яркостью. Каждый составляющий цвет характеризуется своей яркостью. Схема RGB используется для создания графических образов в устройствах, излучающих свет, – мониторах, телевизорах.

В полиграфических системах напечатанный на бумаге графический объект сам не излучает световых волн. В полиграфических системах напечатанный на бумаге графический объект сам не излучает световых волн. Изображение формируется на основе отраженной волны от окрашенных поверхностей. Окрашенные поверхности, на которые подает белый свет должны поглотить все составляющие цвета, кроме того, который мы видим.

Цвет красителя можно получить, красителями, которые поглощают, а не излучают. Цвет красителя можно получить, красителями, которые поглощают, а не излучают. Например, если мы видим зеленое дерево, то это означает что из падающего белого цвета, т.е. суммы красного зеленого синего поглощены красный и синий, а зеленый отражен.

Цвета красителей должны быть дополняющими: Цвета красителей должны быть дополняющими: голубой (Cyan=B+G), дополняющий красного; Пурпурный (Magenta= R+B), дополняющий зеленого; Желтый (Yellow= R+G) дополняющий синего.

Цветные красители по отражающим свойствам не одинаковы, поэтому для повышения контрастности используется черный. Цветные красители по отражающим свойствам не одинаковы, поэтому для повышения контрастности используется черный. Модель CMYK названа по первым буквам слов Cyan, Magenta, Yellow, и последней буквы слова Blak. В этой модели цвета вычитаются.

Цветовая модель HSB HSB — это трехканальная модель цвета. Она получила название по первым буквам английских слов: цветовой тон (hue), насыщенность (saturation), яркость (brightness). Характеризующие параметры цвета. Цветовой тон (собственно цвет). Цветовые тона или спектральные цвета   располагаются на цветовом круге. Цветовой тон характеризуется положением на цветовом круге и определяется величиной угла в диапазоне от 0 до 360 градусов. Эти цвета обладают максимальной насыщенностью и максимальной яркостью.

Цветовая модель HSB Насыщенность (процент добавления к цвету белой краски) — это параметр цвета, определяющий его чистоту. Если по краю цветового круга располагаются максимально насыщенные цвета (100%), то остается только уменьшать их насыщенность до минимума (0%). Цвет с уменьшением насыщенности осветляется, как будто к нему прибавляют белую краску. При значении насыщенности 0% любой цвет становится белым. Яркость (процент добавления черной краски) — это параметр цвета, определяющий освещенность или затемненность цвета. 

Цветовая модель HSB Все цвета рассмотренного выше цветового круга имеют максимальную яркость (100%) и ярче уже быть не могут. Яркость можно уменьшить до минимума (0%). Уменьшение яркости цвета означает его зачернение. Работу с яркостью можно характеризовать как добавление в спектральный цвет определенного процента черной краски. В общем случае, любой цвет получается из спектрального цвета добавлением определенного процента белой и черной красок, то есть фактически серой краски.

Цветовая модель L*a*b Любой цвет данной модели определяется  светлотой (L) двумя хроматическими компонентами: параметром a, который изменяется в диапазоне от зеленого до красного, и параметром b, изменяющимся в диапазоне от синего до желтого Применение.  Программа Adobe Photoshop 5.0 использует L*a*b в качестве модели-посредника при любом конвертировании из модели в модель