Презентация на тему: Изображения в памяти компьютера

Последовательностями 000011100001111 можно закодировать и графическую информацию. Как это сделать?

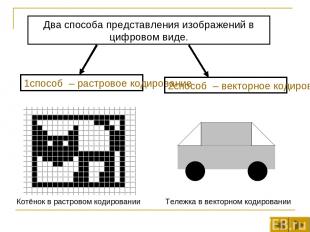
Два способа представления изображений в цифровом виде. 1способ – растровое кодирование 2способ – векторное кодирование Котёнок в растровом кодировании Тележка в векторном кодировании

Рассмотрим 1 способ кодирования. Растровое кодирование. Вы заметили, что графический объект (рисунок 1), подлежащий представлению в цифровом виде, делится вертикальными и горизонтальными линиями на крошечные фрагменты – пиксели. Пиксель – минимальный участок графического изображения, который имеет размер и цвет. Цвет каждого пикселя кодируется двоичным числом. Рисунок 1

Рассмотрим простую черно-белую картинку: каждую пустую (белую) клеточку рисунка, заключённую в рамку, закодируем 1, а закрашенную (черную) - 0 Получим 1111111111100011 0111111011111001 0011110011111100 0000000011111100 0010010011111100 0000000011111100 0000000000000001 1000000100000001 1110011100111001 1111111100111001 1111111000110001 1111111000110001

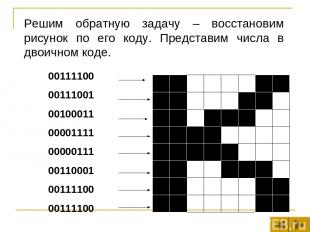
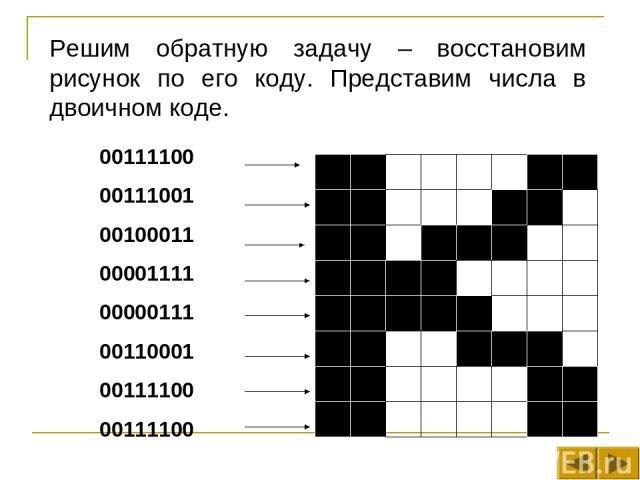
Решим обратную задачу – восстановим рисунок по его коду. Представим числа в двоичном коде. 00111100 00111001 00100011 00001111 00000111 00110001 00111100 00111100

ВЫВОДЫ: При создании черно-белого цифрового рисунка каждый пиксель кодируется 1 битом. 2. При создании цветного цифрового рисунка каждый пиксель кодируется цепочкой из 24-х 0 и 1, что позволяет различать более 16 миллионов цветовых оттенков.

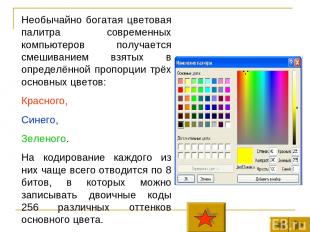
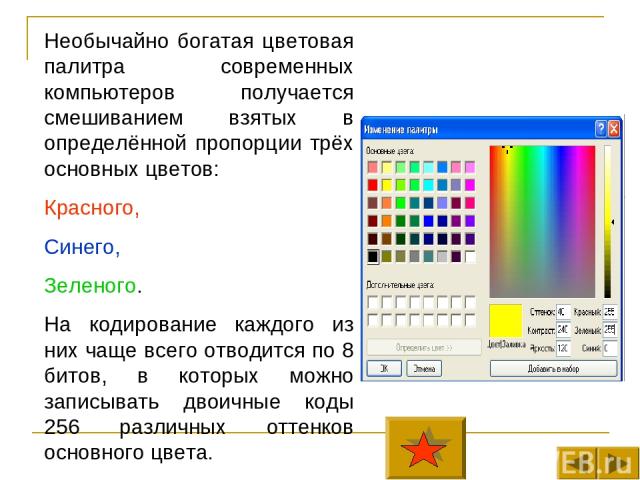
Необычайно богатая цветовая палитра современных компьютеров получается смешиванием взятых в определённой пропорции трёх основных цветов: Красного, Синего, Зеленого. На кодирование каждого из них чаще всего отводится по 8 битов, в которых можно записывать двоичные коды 256 различных оттенков основного цвета.

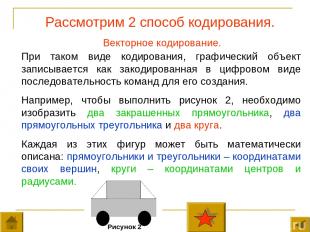
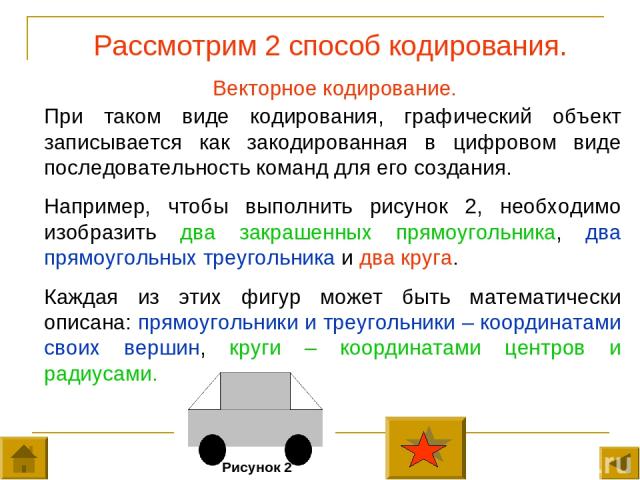
Рассмотрим 2 способ кодирования. Векторное кодирование. При таком виде кодирования, графический объект записывается как закодированная в цифровом виде последовательность команд для его создания. Например, чтобы выполнить рисунок 2, необходимо изобразить два закрашенных прямоугольника, два прямоугольных треугольника и два круга. Каждая из этих фигур может быть математически описана: прямоугольники и треугольники – координатами своих вершин, круги – координатами центров и радиусами. Рисунок 2