Презентация на тему: Интеллектуальные информационные системы 8

Методы поиска решений Курс «Интеллектуальные информационные системы» Лекция 8

Альфа-бета-процедура Теоретически, это эквивалентная минимаксу процедура, с помощью которой всегда получается такой же результат, но заметно быстрее, так как целые части дерева исключаются без проведения анализа. В основе этой процедуры лежит идея Дж. Маккарти об использовании двух переменных, обозначенных α и β (1961 год). Основная идея метода состоит в сравнении наилучших оценок, полученных для полностью изученных ветвей, с наилучшими предполагаемыми оценками для оставшихся. Можно показать, что при определенных условиях некоторые вычисления являются лишними. Рассмотрим идею отсечения на примере

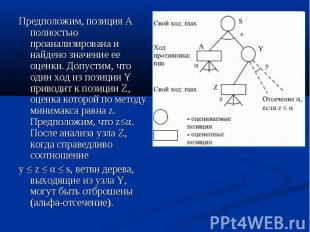
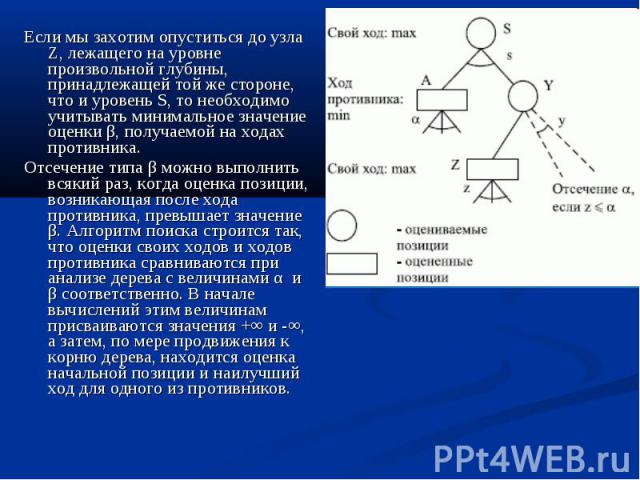
Предположим, позиция А полностью проанализирована и найдено значение ее оценки. Допустим, что один ход из позиции Y приводит к позиции Z, оценка которой по методу минимакса равна z. Предположим, что z≤α. После анализа узла Z, когда справедливо соотношение Предположим, позиция А полностью проанализирована и найдено значение ее оценки. Допустим, что один ход из позиции Y приводит к позиции Z, оценка которой по методу минимакса равна z. Предположим, что z≤α. После анализа узла Z, когда справедливо соотношение y ≤ z ≤ α ≤ s, ветви дерева, выходящие из узла Y, могут быть отброшены (альфа-отсечение).

Если мы захотим опуститься до узла Z, лежащего на уровне произвольной глубины, принадлежащей той же стороне, что и уровень S, то необходимо учитывать минимальное значение оценки β, получаемой на ходах противника. Если мы захотим опуститься до узла Z, лежащего на уровне произвольной глубины, принадлежащей той же стороне, что и уровень S, то необходимо учитывать минимальное значение оценки β, получаемой на ходах противника. Отсечение типа β можно выполнить всякий раз, когда оценка позиции, возникающая после хода противника, превышает значение β. Алгоритм поиска строится так, что оценки своих ходов и ходов противника сравниваются при анализе дерева с величинами α и β соответственно. В начале вычислений этим величинам присваиваются значения +∞ и -∞, а затем, по мере продвижения к корню дерева, находится оценка начальной позиции и наилучший ход для одного из противников.

Правила вычисления α и β в процессе поиска рекомендуются следующие: у MAX вершины значение α равно наибольшему в данный момент значению среди окончательных возвращенных значений для ее дочерних вершин; у MIN вершины значение β равно наименьшему в данный момент значению среди окончательных возвращенных значений для ее дочерних вершин.

Правила прекращения поиска: можно не проводить поиска на поддереве, растущем из всякой MIN вершины, у которой значение β не превышает значения α всех ее родительских MAX вершин; можно не проводить поиска на поддереве, растущем из всякой MAX вершины, у которой значение α не меньше значения β всех ее родительских MIN вершин.

На рис. показаны α -β отсечения для конкретного примера. Таким образом, α -β-алгоритм дает тот же результат, что и метод минимакса, но выполняется быстрее. На рис. показаны α -β отсечения для конкретного примера. Таким образом, α -β-алгоритм дает тот же результат, что и метод минимакса, но выполняется быстрее.

Использование алгоритмов эвристического поиска для поиска на графе И, ИЛИ выигрышной стратегии в более сложных задачах и играх (шашки, шахматы) не реален. По некоторым оценкам игровое дерево игры в шашки содержит 1040 вершин, в шахматах 10120 вершин. Если при игре в шашки для одной вершины требуется 1/3 наносекунды, то всего игрового времени потребуется 1021 веков. В таких случаях вводятся искусственные условия остановки, основанные на таких факторах, как наибольшая допустимая глубина вершин в дереве поиска или ограничения на время и объем памяти. Использование алгоритмов эвристического поиска для поиска на графе И, ИЛИ выигрышной стратегии в более сложных задачах и играх (шашки, шахматы) не реален. По некоторым оценкам игровое дерево игры в шашки содержит 1040 вершин, в шахматах 10120 вершин. Если при игре в шашки для одной вершины требуется 1/3 наносекунды, то всего игрового времени потребуется 1021 веков. В таких случаях вводятся искусственные условия остановки, основанные на таких факторах, как наибольшая допустимая глубина вершин в дереве поиска или ограничения на время и объем памяти. Многие из рассмотренных выше идей были использованы А. Ньюэллом, Дж. Шоу и Г. Саймоном в их программе GPS. Процесс работы GPS в общем воспроизводит методы решения задач, применяемые человеком: выдвигаются подцели, приближающие к решению; применяется эвристический метод (один, другой и т. д.), пока не будет получено решение. Попытки прекращаются, если получить решение не удается. Программа STRIPS (STanford Research Institut Problem Solver) вырабатывает соответствующий порядок действий робота в зависимости от поставленной цели. Программа способна обучаться на опыте решения предыдущих задач. Большая часть игровых программ также обучается в процессе работы. Например, знаменитая шашечная программа Самюэля, выигравшая в 1974 году у чемпиона мира, "заучивала наизусть" выигранные партии и обобщала их для извлечения пользы из прошлого опыта. Программа HACHER Зуссмана, управляющая поведением робота, обучалась также и на ошибках.

Методы поиска решений на основе исчисления предикатов Семантика исчисления предикатов обеспечивает основу для формализации логического вывода. Возможность логически выводить новые правильные выражения из набора истинных утверждений очень важна. Логически выведенные утверждения корректны, и они совместимы со всеми предыдущими интерпретациями первоначального набора выражений.

В исчислении высказываний основным объектом является переменное высказывание (предикат), истинность или ложность которого зависит от значений входящих в него переменных. Так, истинность предиката "x был физиком" зависит от значения переменной x. Если x - П. Капица, то предикат истинен, если x - М. Лермонтов, то он ложен. В исчислении высказываний основным объектом является переменное высказывание (предикат), истинность или ложность которого зависит от значений входящих в него переменных. Так, истинность предиката "x был физиком" зависит от значения переменной x. Если x - П. Капица, то предикат истинен, если x - М. Лермонтов, то он ложен. На языке исчисления предикатов утверждение x(P(x) Q(x)) читается так: "для любого x если P(x), то имеет место и Q(x)". Иногда его записывают и так: x (P(x) → Q(x)). Выделенное подмножество тождественно истинных формул (или правильно построенных формул - ППФ), истинность которых не зависит от истинности входящих в них высказываний, называется аксиомами.

В исчислении предикатов имеется множество правил вывода. В качестве примера приведем классическое правило отделения, или modus ponens : В исчислении предикатов имеется множество правил вывода. В качестве примера приведем классическое правило отделения, или modus ponens : (A, A → B) / B которое читается так "если истинна формула A и истинно, что из A следует B, то истинна и формула B". Формулы, находящиеся над чертой, называются посылками вывода, а под чертой - заключением. Это правило вывода формализует основной закон дедуктивных систем: из истинных посылок всегда следуют истинные заключения. Аксиомы и правила вывода исчисления предикатов первого порядка задают основу формальной дедуктивной системы, в которой происходит формализация схемы рассуждений в логическом программировании.

Другие правила вывода: Modus tollendo tollens : Если из A следует B и B ложно, то и A ложно. Modus ponendo tollens : Если A и B не могут одновременно быть истинными и A истинно, то B ложно. Modus tollendo ponens : Если либо A, либо B является истинным и A не истинно, то B истинно.

Решаемая задача представляется в виде утверждений (аксиом) f1, F2... Fn исчисления предикатов первого порядка. Цель задачи B также записывается в виде утверждения, справедливость которого следует установить или опровергнуть на основании аксиом и правил вывода формальной системы. Тогда решение задачи (достижение цели задачи) сводится к выяснению логического следования (выводимости) целевой формулы B из заданного множества формул (аксиом) f1, F2... Fn. Такое выяснение равносильно доказательству общезначимости (тождественно-истинности) формулы Решаемая задача представляется в виде утверждений (аксиом) f1, F2... Fn исчисления предикатов первого порядка. Цель задачи B также записывается в виде утверждения, справедливость которого следует установить или опровергнуть на основании аксиом и правил вывода формальной системы. Тогда решение задачи (достижение цели задачи) сводится к выяснению логического следования (выводимости) целевой формулы B из заданного множества формул (аксиом) f1, F2... Fn. Такое выяснение равносильно доказательству общезначимости (тождественно-истинности) формулы f1& F2&... & Fn → B или невыполнимости (тождественно-ложности) формулы f1& F2&... & Fn& ¬B

Из практических соображений удобнее использовать доказательство от противного, то есть доказывать невыполнимость формулы. На доказательстве от противного основано и ведущее правило вывода, используемое в логическом программировании, - принцип резолюции. Робинсон открыл более сильное правило вывода, чем modus ponens, которое он назвал принципом резолюции (или правилом резолюции ). При использовании принципа резолюции формулы исчисления предикатов с помощью несложных преобразований приводятся к так называемой дизъюнктивной форме, то есть представляются в виде набора дизъюнктов. При этом под дизъюнктом понимается дизъюнкция литералов, каждый из которых является либо предикатом, либо отрицанием предиката. Из практических соображений удобнее использовать доказательство от противного, то есть доказывать невыполнимость формулы. На доказательстве от противного основано и ведущее правило вывода, используемое в логическом программировании, - принцип резолюции. Робинсон открыл более сильное правило вывода, чем modus ponens, которое он назвал принципом резолюции (или правилом резолюции ). При использовании принципа резолюции формулы исчисления предикатов с помощью несложных преобразований приводятся к так называемой дизъюнктивной форме, то есть представляются в виде набора дизъюнктов. При этом под дизъюнктом понимается дизъюнкция литералов, каждый из которых является либо предикатом, либо отрицанием предиката.

Пример дизъюнкта: Пример дизъюнкта: x (P(x, c1) Q(x, c2)). Пусть P - предикат уважать, c1 - Ключевский, Q - предикат знать,c2 - история. Теперь данный дизъюнкт отражает факт "каждый, кто знает историю, уважает Ключевского". Еще один пример дизъюнкта: x (P(x, c1)& P(x, c2)). Пусть P - предикат знать, c1 - физика, c2 - история. Данный дизъюнкт отражает запрос "кто знает физику и историю одновременно".

Таким образом, условия решаемых задач (факты) и целевые утверждения задач (запросы) можно выразить в дизъюнктивной форме логики предикатов первого порядка. В дизъюнктах кванторы всеобщности , , обычно опускаются, а связки Л, ¬, заменяются на → импликацию. Таким образом, условия решаемых задач (факты) и целевые утверждения задач (запросы) можно выразить в дизъюнктивной форме логики предикатов первого порядка. В дизъюнктах кванторы всеобщности , , обычно опускаются, а связки Л, ¬, заменяются на → импликацию.

Принцип резолюции Главная идея этого правила вывода заключается в проверке того, содержит ли множество дизъюнктов R пустой (ложный) дизъюнкт. Обычно резолюция применяется с прямым или обратным методом рассуждения. Прямой метод из посылок A, A→ B выводит заключение B (правило modus ponens). Основной недостаток прямого метода состоит в его ненаправленности: повторное применение метода приводит к резкому росту промежуточных заключений, не связанных с целевым заключением. Обратный вывод является направленным: из желаемого заключения B и тех же посылок он выводит новое подцелевое заключение A. Каждый шаг вывода в этом случае связан всегда с первоначально поставленной целью. Существенный недостаток метода резолюции заключается в формировании на каждом шаге вывода множества резольвент - новых дизъюнктов, большинство из которых оказывается лишними. В связи с этим разработаны различные модификации принципа резолюции, использующие более эффективные стратегии поиска и различного рода ограничения на вид исходных дизъюнктов. В этом смысле наиболее удачной и популярной является система ПРОЛОГ, которая использует специальные виды дизъюнктов, называемых дизъюнктами Хорна.

Процесс доказательства методом резолюции (от обратного) состоит из следующих этапов: Предложения или аксиомы приводятся к дизъюнктивной нормальной форме. К набору аксиом добавляется отрицание доказываемого утверждения в дизъюнктивной форме. Выполняется совместное разрешение этих дизъюнктов, в результате чего получаются новые основанные на них дизъюнктивные выражения (резольвенты). Генерируется пустое выражение, означающее противоречие. Подстановки, использованные для получения пустого выражения, свидетельствуют о том, что отрицание отрицания истинно.

Примеры применения методов поиска решений на основе исчисления предикатов.

Одно из возможных доказательств (их более одного) дает следующую последовательность резольвент: ¬happy(Z)резольвента 6 и 4 poor(X) Л ¬smart(X)резольвента 7 и 1 poor(Y) Л ¬read(Y)резольвента 8 и 2 ¬read(John)резольвента 9 и 3b NIL резольвента 10 и 3a Символ NIL означает, что база данных выражений содержит противоречие и поэтому наше предположение, что не существует человек, живущий интересной жизнью, неверно.

В методе резолюции порядок комбинации дизъюнктивных выражений не устанавливался. Значит, для больших задач будет наблюдаться экспоненциальный рост числа возможных комбинаций. Поэтому в процедурах резолюции большое значение имеют также эвристики поиска и различные стратегии. Одна из самых простых и понятных стратегий - стратегия предпочтения единичного выражения, которая гарантирует, что резольвента будет меньше, чем наибольшее родительское выражение. Ведь в итоге мы должны получить выражение, не содержащее литералов вообще.

Среди других стратегий (поиск в ширину (breadth-first), стратегия "множества поддержки", стратегия линейной входной формы) стратегия "множества поддержки" показывает отличные результаты при поиске в больших пространствах дизъюнктивных выражений. Суть стратегии такова. Для некоторого набора исходных дизъюнктивных выражений S можно указать подмножество T, называемое множеством поддержки. Для реализации этой стратегии необходимо, чтобы одна из резольвент в каждом опровержении имела предка из множества поддержки. Можно доказать, что если S - невыполнимый набор дизъюнктов, а S-T - выполнимый, то стратегия множества поддержки является полной в смысле опровержения. Среди других стратегий (поиск в ширину (breadth-first), стратегия "множества поддержки", стратегия линейной входной формы) стратегия "множества поддержки" показывает отличные результаты при поиске в больших пространствах дизъюнктивных выражений. Суть стратегии такова. Для некоторого набора исходных дизъюнктивных выражений S можно указать подмножество T, называемое множеством поддержки. Для реализации этой стратегии необходимо, чтобы одна из резольвент в каждом опровержении имела предка из множества поддержки. Можно доказать, что если S - невыполнимый набор дизъюнктов, а S-T - выполнимый, то стратегия множества поддержки является полной в смысле опровержения. Исследования, связанные с доказательством теорем и разработкой алгоритмов опровержения резолюции, привели к развитию языка логического программирования PROLOG (Programming in Logic). PROLOG основан на теории предикатов первого порядка. Логическая программа - это набор спецификаций в рамках формальной логики. Несмотря на то, что в настоящее время удельный вес языков LISP и PROLOG снизился и при решении задач ИИ все больше используются C, C++ и Java, однако многие задачи и разработка новых методов решения задач ИИ продолжают опираться на языки LISP и PROLOG. Рассмотрим одну из таких задач - задачу планирования последовательности действий и ее решение на основе теории предикатов.

Задачи планирования последовательности действий Рассмотрим ряд предикатов, необходимых для работы планировщика из мира блоков. Имеется некоторый робот, являющийся подвижной рукой, способной брать и перемещать кубики.

Рука робота может выполнять следующие задания (U, V, W, X, Y, Z - переменные). goto(X,Y,Z)перейти в местоположение X,Y,Z pickup(W)взять блок W и держать его putdown(W)опустить блок W в некоторой точке stack(U,V)поместить блок U на верхнюю грань блока V unstack(U,V)убрать блок U с верхней грани блока V Состояния мира описываются следующим множеством предикатов и отношений между ними. on(X,Y)блок X находится на верхней грани блока Y clear(X)верхняя грань блока Х пуста gripping(X)захват робота удерживает блок Х gripping()захват робота пуст ontable(W)блок W находится на столе

Требуется построить последовательность действий робота, ведущую (при ее реализации) к достижению целевого состояния. Требуется построить последовательность действий робота, ведущую (при ее реализации) к достижению целевого состояния. Состояния мира кубиков представим в виде предикатов. Начальное состояние можно описать следующим образом: где: handempty означает, что рука робота Робби пуста.

Целевое состояние записывается так: Целевое состояние записывается так: goal = [handempty, ontable(a), ontable(b), on(c,b), clear(a), clear(c)] Правила, воздействующие на состояния и приводящие к новым состояниям ( X) (pickup(X)→ (gripping(X) ← (gripping() Л clear(X)Л ontable(X)))) ( X) (putdown(X) →((gripping()Л ontable(X) Л clear(X)) ← gripping(X))) ( X) ( Y) (stack(X,Y) →((on(X,Y) Л gripping() Л clear(X)) ← (clear(Y) Л gripping(X)))) ( X) ( Y) (unstack(X,Y) → ((clear(Y) Л gripping(X)) ← (on(X,Y) Л clear(X) Л gripping()))

Прежде чем использовать эти правила, необходимо упомянуть о проблеме границ. При выполнении некоторого действия могут изменяться другие предикаты и для этого могут использоваться аксиомы границ - правила, определяющие инвариантные предикаты. Одно из решений этой проблемы предложено в системе STRIPS. Прежде чем использовать эти правила, необходимо упомянуть о проблеме границ. При выполнении некоторого действия могут изменяться другие предикаты и для этого могут использоваться аксиомы границ - правила, определяющие инвариантные предикаты. Одно из решений этой проблемы предложено в системе STRIPS. В начале 1970-х годов в Стэнфордском исследовательском институте (Stanford Research Institute Planning System) была создана система STRIPS для управления роботом. В STRIPS четыре оператора pickup, putdown, stack,unstack описываются тройками элементов. Первый элемент тройки - множество предусловий (П), которым удовлетворяет мир до применения оператора. Второй элемент тройки - список дополнений (Д), которые являются результатом применения оператора. Третий элемент тройки - список вычеркиваний (В), состоящий из выражений, которые удаляются из описания состояния после применения оператора.

Ведя рассуждения для рассматриваемого примера от начального состояния, мы приходим к поиску в пространстве состояний. Требуемая последовательность действий (план достижения цели) будет следующей: Ведя рассуждения для рассматриваемого примера от начального состояния, мы приходим к поиску в пространстве состояний. Требуемая последовательность действий (план достижения цели) будет следующей: unstack(A,B), putdown(A), pickup(C), stack(C,B) Для больших графов (сотни состояний) поиск следует проводить с использованием оценочных функций. Заключение: планирование достижения цели можно рассматривать как поиск в пространстве состояний. Для нахождения пути из начального состояния к целевому (плана последовательности действий робота) могут применяться методы поиска в пространстве состояний с использованием исчисления предикатов.

Поиск решений в системах продукций Поиск решений в системах продукций наталкивается на проблемы выбора правил из конфликтного множества, как это указывалось в предыдущей лекции. Различные варианты решения этой проблемы рассмотрим на примере ЭСО CLIPS, на которой нам предстоит в 7 лекции разработать исследовательский прототип ЭС. Правила в ЭС, кроме фактора уверенности эксперта, имеют приоритет выполнения (salience). Конфликтное множество (КМ) - это список всех правил, имеющих удовлетворенные условия при некотором, текущем состоянии списка фактов и объектов и которые еще не были выполнены. Как отмечалось ранее, конфликтное множество это простейшая база целей. Когда активизируется новое правило с определенным приоритетом, оно помещается в список правил КМ ниже всех правил с большим приоритетом и выше всех правил с меньшим приоритетом. Правила с высшим приоритетом выполняются в первую очередь. Среди правил с одинаковым приоритетом используется определенная стратегия.

CLIPS поддерживает семь стратегий разрешения конфликтов. CLIPS поддерживает семь стратегий разрешения конфликтов. Стратегия глубины (depth strategy) является стратегией по умолчанию (default strategy) в CLIPS. Только что активизированное правило помещается поверх всех правил с таким же приоритетом. Это позволяет реализовать поиск в глубину. Стратегия ширины (breadth strategy) - только что активизированное правило помещается ниже всех правил с таким же приоритетом. Это, в свою очередь, реализует поиск в ширину. LEX стратегия - активация правила, выполненная более новыми образцами (фактами), располагается перед активацией, осуществленной более поздними образцами. Например, как это указано в таблице ниже. MEA стратегия - сортировка образцов не производится, а осуществляется только упорядочение правил по первым образцам, как это показано в столбце 3 таблицы.

Результаты применения LEX и MEA стратегий

Стратегия упрощения (simplicity strategy) - среди всех правил с одинаковым приоритетом только что активизированное правило располагается выше всех правил с равной или большей определенностью (specificity). Определенность правила задается количеством сопоставлений в левой части правил плюс количество вызовов функций. Логические функции не увеличивают определенность правила. Стратегия упрощения (simplicity strategy) - среди всех правил с одинаковым приоритетом только что активизированное правило располагается выше всех правил с равной или большей определенностью (specificity). Определенность правила задается количеством сопоставлений в левой части правил плюс количество вызовов функций. Логические функции не увеличивают определенность правила. Стратегия усложнения (complexity strategy) - среди всех правил с одинаковым приоритетом только что активизированное правило располагается выше всех правил с равной или большей определенностью. Случайная стратегия (random strategy) - каждой активации назначается случайное число, которое используется для определения местоположения среди активаций с определенным приоритетом.

Подход на основе стратегий поиска решений в продукционных ЭС известен достаточно давно. Весьма популярная в начале 90-х годов ЭСО GURU (ИНТЕР-ЭКСПЕРТ) также использовала подобные механизмы управления стратегиями поиска. Возможность смены стратегии в ходе решения задачи программным образом и накопление опыта, какие стратегии дают лучшие результаты для определенных классов задач, позволяет получить эффективные механизмы поиска решений в СПЗ на основе продукций. Подход на основе стратегий поиска решений в продукционных ЭС известен достаточно давно. Весьма популярная в начале 90-х годов ЭСО GURU (ИНТЕР-ЭКСПЕРТ) также использовала подобные механизмы управления стратегиями поиска. Возможность смены стратегии в ходе решения задачи программным образом и накопление опыта, какие стратегии дают лучшие результаты для определенных классов задач, позволяет получить эффективные механизмы поиска решений в СПЗ на основе продукций. Заключение: существуют различные методы поиска решений в семантических сетях, например, метод обхода семантической сети - мультипарсинг. Данный метод оригинален тем, что позволяет параллельно "вести" по графу несколько маркеров и, тем самым, распараллеливать процесс поиска информации в семантической сети, что увеличивает скорость поиска. Эти методы используются, как правило, при представлении текста в виде объектно-ориентированной семантической сети

Распознавание изображений

Общая характеристика задач распознавания образов и их типы Под образом понимается структурированное описание изучаемого объекта или явления, представленное вектором признаков, каждый элемент которого представляет числовое значение одного из признаков, характеризующих соответствующий объект. Общая структура системы распознавания и этапы в процессе ее разработки показаны на рис

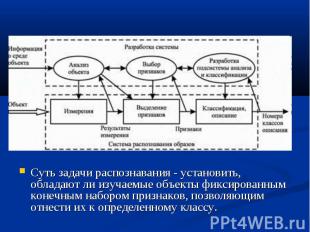
Суть задачи распознавания - установить, обладают ли изучаемые объекты фиксированным конечным набором признаков, позволяющим отнести их к определенному классу. Суть задачи распознавания - установить, обладают ли изучаемые объекты фиксированным конечным набором признаков, позволяющим отнести их к определенному классу.

Задачи распознавания имеют следующие характерные черты. Это информационные задачи, состоящие из двух этапов: а) приведение исходных данных к виду, удобному для распознавания; б) собственно распознавание (указание принадлежности объекта определенному классу). В этих задачах можно вводить понятие аналогии или подобия объектов и формулировать понятие близости объектов в качестве основания для зачисления объектов в один и тот же класс или разные классы. В этих задачах можно оперировать набором прецедентов-примеров, классификация которых известна и которые в виде формализованных описаний могут быть предъявлены алгоритму распознавания для настройки на задачу в процессе обучения. Для этих задач трудно строить формальные теории и применять классические математические методы (часто недоступна информация для точной математической модели или выигрыш от использования модели и математических методов не соизмерим с затратами). В этих задачах возможна "плохая" информация (информация с пропусками, разнородная, косвенная, нечеткая, неоднозначная, вероятностная).

Типы задач распознавания Задача распознавания - отнесение предъявленного объекта по его описанию к одному из заданных классов (обучение с учителем). Задача автоматической классификации - разбиение множества объектов (ситуаций) по их описаниям на систему непересекающихся классов (таксономия, кластерный анализ, обучение без учителя). Задача выбора информативного набора признаков при распознавании. Задача приведения исходных данных к виду, удобному для распознавания. Динамическое распознавание и динамическая классификация - задачи 1 и 2 для динамических объектов. Задача прогнозирования - это задачи 5, в которых решение должно относиться к некоторому моменту в будущем.

Основы теории анализа и распознавания изображений

Рассмотрим алгоритмы распознавания, основанные на вычислении оценок. В их основе лежит принцип прецедентности (в аналогичных ситуациях следует действовать аналогично). Рассмотрим алгоритмы распознавания, основанные на вычислении оценок. В их основе лежит принцип прецедентности (в аналогичных ситуациях следует действовать аналогично). Пусть задан полный набор признаков x1, ..., xN. Выделим систему подмножеств множества признаков S1, ..., Sk. Удалим произвольный набор признаков из строк ω1, ω2, ..., ωrm и обозначим полученные строки через Sω1, Sω2, ..., Sωrm, Sω' .

Проиллюстрируем описанный алгоритм распознавания на примере. Задано 10 классов объектов. Требуется определить признаки таблицы обучения, пороги и построить оценки близости для классов объектов, показанных на рисунке. Предлагаются следующие признаки таблицы обучения: Проиллюстрируем описанный алгоритм распознавания на примере. Задано 10 классов объектов. Требуется определить признаки таблицы обучения, пороги и построить оценки близости для классов объектов, показанных на рисунке. Предлагаются следующие признаки таблицы обучения: x1- количество вертикальных линий минимального размера; x2- количество горизонтальных линий; x3- количество наклонных линий; x4- количество горизонтальных линий снизу объекта.

Пример задачи по распознаванию Таблица обучения для задачи по распознаванию

Распознавание по методу аналогий Этот метод очень хорошо знаком студентам (знание решения аналогичной задачи помогает в решении текущей задачи). Рассмотрим этот метод на примере задачи П. Уинстона по поиску геометрических аналогий, представленном на рис. Среди фигур второго ряда требуется выбрать X {1, 2, 3, 4, 5} такое, что A так соотносится с B, как C соотносится с X, и такое, которое лучше всего при этом подходит. Для решения задачи необходимо понять, в чем разница между фигурами A и B (наличие/отсутствие жирной точки), и после этого ясно, что лучше всего для C подходит X=3 . Решение таких задач предполагает описание изображения и преобразования (отношения между фигурами на изображениях), а также описание изменения отдельных фигур, составление правил и оценка изменений.

В качестве примера запишем три правила, показывающие, каким образом одно изображение (исходное) становится результирующим. В качестве примера запишем три правила, показывающие, каким образом одно изображение (исходное) становится результирующим. Правило 1 (исходное изображение):k выше m, k выше n, n внутри m Правило 2 (результир. изображение):n слева m Правило 3 (масшабирование, повороты): k исчезло m изменение масштаба 1:1, вращение 00 n изменение масштаба 1:2, вращение 00

Важные моменты при таких преобразованиях В исходном и результирующем изображениях допускаются отношения ВЫШЕ, ВНУТРИ, СЛЕВА, В результате преобразования изображение может стать МЕНЬШЕ, БОЛЬШЕ, испытать ПОВОРОТ или ВРАЩЕНИЕ, ОТРАЖЕНИЕ, УДАЛЕНИЕ, ДОБАВЛЕНИЕ. Написание правил лучше всего начинать с проведения диагональных линий через центры фигур. Лишние отношения (СПРАВА ОТ и СЛЕВА ОТ, ВЫШЕ и НИЖЕ, ИЗНУТРИ и СНАРУЖИ,) использовать не рекомендуется.

Пример задачи распознавания по аналогии Разные виды преобразований могут иметь различные веса, например, исчезновению фигуры целесообразно назначить больший вес, чем преобразованию масштаба; а вращение фигуры может иметь меньший вес, чем отражение.

Методы распознавания по аналогии могут быть эффективнее, если используется обучение. Различают обучение с учителем, обучение по образцу (эталону) и др. виды обучения. Суть идеи такова. Программе распознавания предъявляется объект, например, арка. Программа создает внутреннюю модель: Методы распознавания по аналогии могут быть эффективнее, если используется обучение. Различают обучение с учителем, обучение по образцу (эталону) и др. виды обучения. Суть идеи такова. Программе распознавания предъявляется объект, например, арка. Программа создает внутреннюю модель: (арка (компонент1 (назначение (опора)) (тип (брусок))) (компонент2 (назначение (опора)) (тип (брусок))) (компонент3 (назначение (перекладина)) (тип (брусок)) (поддерживается (компонент1), (компонент2)))

После этого предъявляется другой объект и говорится, что это тоже арка. Программа вынуждена дополнить свою внутреннюю модель: После этого предъявляется другой объект и говорится, что это тоже арка. Программа вынуждена дополнить свою внутреннюю модель: (арка (компонент1 (назначение (опора)) (тип (брусок))) (компонент2 (назначение (опора)) (тип (брусок))) (компонент3 (назначение (перекладина)) (тип (брусок) или (клин) ) (поддерживается (компонент1), (компонент2))) После такого обучения система распознавания будет узнавать в качестве арки как первый, так и второй объект.

Актуальные задачи распознавания Среди множества интересных задач по распознаванию (распознавание отпечатков пальцев, распознавание по радужной оболочке глаза, распознавание машиностроительных чертежей и т. д.) следует выделить задачу определения реальных координат заготовки и определения шероховатости обрабатываемой поверхности. Другой актуальной задачей является распознавание машинописных и рукописных текстов в силу ее повседневной необходимости. Практическое значение задачи машинного чтения печатных и рукописных текстов определяется необходимостью представления, хранения и использования в электронном виде огромного количества накопленной и вновь создающейся текстовой информации. Кроме того, большое значение имеет оперативный ввод в информационные и управляющие системы информации с машиночитаемых бланков, содержащих как напечатанные, так и рукописные тексты.

Для решения данной задачи используются следующие основные принципы. Принцип целостности - распознаваемый объект рассматривается как единое целое, состоящее из структурных частей, связанных между собой пространственными отношениями. Принцип двунаправленности - создание модели ведется от изображения к модели и от модели к изображению. Принцип предвидения заключается в формировании гипотезы о содержании изображения. Гипотеза возникает при взаимодействии процесса "сверху-вниз", разворачивающегося на основе модели среды, модели текущей ситуации и текущего результата восприятия, и процесса "снизу-вверх", основанного на непосредственном грубом признаковом восприятии. Принцип целенаправленности, включающий сегментацию изображения и совместную интерпретацию его частей. Принцип "не навреди" - ничего не делать до распознавания и вне распознавания, то есть без "понимания". Принцип максимального использования модели проблемной среды.

Указанные принципы реализованы в пакете программ "Графит" , в программах FineReader-рукопись и FormReader - для распознавания рукописных символов и, частично, в программе FineReader для распознавания печатных текстов. Входящая в FormReader программа чтения рукописных текстов была выпущена в 1998 году одновременно с системой ABBYY FineReader 4.0. Эта программа может читать все рукописные строчные и заглавные символы, допускает ограниченные соприкосновения символов между собой и с графическими линиями и обеспечивает поддержку 10 языков. Основное применение программы - распознавание и ввод информации с машиночитаемых бланков. Указанные принципы реализованы в пакете программ "Графит" , в программах FineReader-рукопись и FormReader - для распознавания рукописных символов и, частично, в программе FineReader для распознавания печатных текстов. Входящая в FormReader программа чтения рукописных текстов была выпущена в 1998 году одновременно с системой ABBYY FineReader 4.0. Эта программа может читать все рукописные строчные и заглавные символы, допускает ограниченные соприкосновения символов между собой и с графическими линиями и обеспечивает поддержку 10 языков. Основное применение программы - распознавание и ввод информации с машиночитаемых бланков. В системе ABBYY FormReader при распознавании рукописных текстов используются структурный, растровый, признаковый, дифференциальный и лингвистический уровни распознавания.