Презентация на тему: Многоугольгики

Презентацию подготовила Презентацию подготовила учитель математики и информатики Гатауллина Элла Равильевна Муниципальное общеобразовательное учреждение «Заинская средняя общеобразовательная школа № 6» Заинского муниципального района Республики Татарстан Город Заинск, РТ


Ввести понятие многоугольника, выпуклого многоугольника. Ввести понятие многоугольника, выпуклого многоугольника. Ввести формулу суммы углов выпуклого многоугольника и суммы углов четырехугольника.
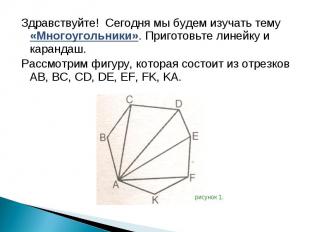
Здравствуйте! Сегодня мы будем изучать тему «Многоугольники». Приготовьте линейку и карандаш. Здравствуйте! Сегодня мы будем изучать тему «Многоугольники». Приготовьте линейку и карандаш. Рассмотрим фигуру, которая состоит из отрезков AB, BC, CD, DE, EF, FK, KA.

Фигура ABCDEFK на рисунке 1 называется многоугольником (семиугольником), если его смежные отрезки (т.е. отрезки AB и BC, BC и CD, CD и DE, и т. д.) не лежат на одной прямой, а несмежные (т.е. отрезки AB и CD, BC и DE, и т. д.) не имеют общих точек. Фигура ABCDEFK на рисунке 1 называется многоугольником (семиугольником), если его смежные отрезки (т.е. отрезки AB и BC, BC и CD, CD и DE, и т. д.) не лежат на одной прямой, а несмежные (т.е. отрезки AB и CD, BC и DE, и т. д.) не имеют общих точек. Многоугольник с n- вершинами называется n – угольником. Он имеет n сторон.

Отрезки: AB, BC, CD, DE, EF, FK, KA – называются сторонами многоугольника. Отрезки: AB, BC, CD, DE, EF, FK, KA – называются сторонами многоугольника. Точки: A, B, C, D, E, F, K – называются вершинами многоугольника. Точки А и В – соседними вершинами. Отрезки АС, AD, AE, AF – диагоналями многоугольника.
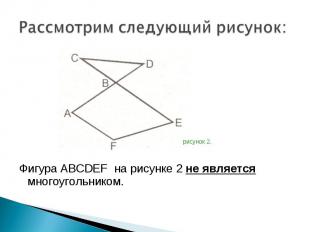
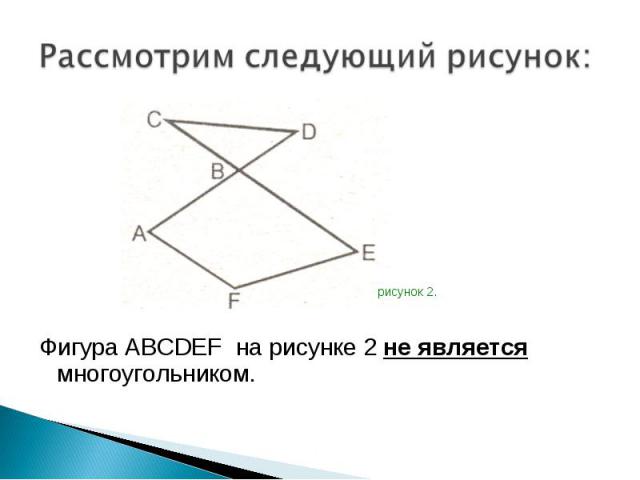
Фигура ABCDEF на рисунке 2 не является многоугольником. Фигура ABCDEF на рисунке 2 не является многоугольником.

Из рисунка 3 ты поймешь, какая часть многоугольника называется внешней областью, а какая внутренней областью. Из рисунка 3 ты поймешь, какая часть многоугольника называется внешней областью, а какая внутренней областью.
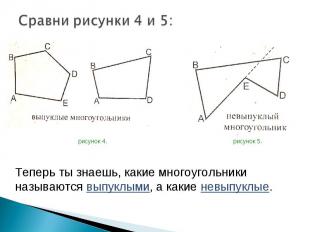
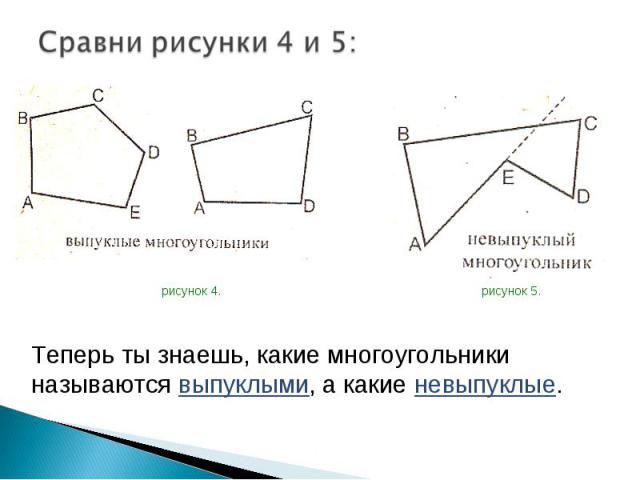
рисунок 4. рисунок 5. рисунок 4. рисунок 5.

Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
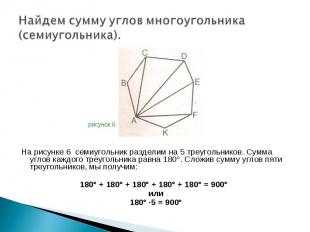
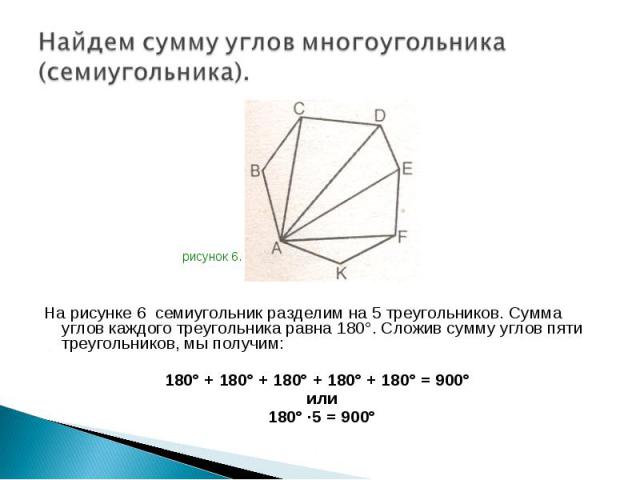
На рисунке 6 семиугольник разделим на 5 треугольников. Сумма углов каждого треугольника равна 180°. Сложив сумму углов пяти треугольников, мы получим: На рисунке 6 семиугольник разделим на 5 треугольников. Сумма углов каждого треугольника равна 180°. Сложив сумму углов пяти треугольников, мы получим: 180° + 180° + 180° + 180° + 180° = 900° или 180° ·5 = 900°

180° · (n – 2) 180° · (n – 2) Запомни эту формулу и применяй при вычислении сумм углов любого выпуклого многоугольника.

1. Среди всех фигур, изображенных на рисунке 7, укажи те, которые являются: 1. Среди всех фигур, изображенных на рисунке 7, укажи те, которые являются: А) многоугольниками; Б) выпуклыми многоугольниками; В) невыпуклыми многоугольниками.

Начерти выпуклый пятиугольник, запиши: Начерти выпуклый пятиугольник, запиши: А) вершины многоугольника; Б) стороны многоугольника; В) диагонали многоугольника; Г) вычисли сумму углов пятиугольника.

выучи определения, формулу и выполни задания из учебника выучи определения, формулу и выполни задания из учебника №№ 364 (а, б), 365 (а, б).

Л.С.Атанасян «Геометрия, 7-9», М.: Просвещение, 2003. Л.С.Атанасян «Геометрия, 7-9», М.: Просвещение, 2003. Б.Г.Зив и др. «Задачи по геометрии для 7-11 классов», М.: Просвещение, 1991.