Презентация на тему: Задачи по динамике

План решения задач по динамике 1. Сделать рисунок, на котором обозначить направление координатных осей, ускорения и всех сил, приложенных к телу . 2. Для каждого тела записать в векторном виде уравнение второго закона Ньютона, перечислив в его правой части в любом порядке все силы, приложенные к телу 3. Записать полученные в п. 2 уравнения в проекции на оси координат. 5. Найти численное значение неизвестной величины, если этого требует условие задачи. 4. Из полученного уравнения (системы уравнений) выразить неизвестную величину.

Движение тел в горизонтальном направлении Какая горизонтальная сила потребуется, чтобы тело массой 2 кг, лежащее на горизонтальной поверхности, начало скользить по ней с ускорением 0,2 м/с2 ? Коэффициент трения принять равным 0,02. Дано: m=2 кг μ = 0,02 а = 0,2 м/с2 F - ? Решение: 1 mg Fтр N F а X ma = mg + Fтр + N + F 3 Ох : ma = 0 - Fтр + 0 + F (1) Оу : 0 = - mg + 0 + N + 0 (2) из (2) : mg =N , т. к. Fтр = μN , получим уравнение (1) в виде: ma = -μmg+ F Откуда F = ma + μmg 4 2 5 Вычислим F= 0,79 Н Ответ: F= 0,79 Н у

Вспомним законы Ньютона I закон: Существуют такие системы отсчета относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела , или действия других тел скомпенсированы. Комментарии: если тело движется с равномерно, это значит, что равнодействующая сил, приложенных к телу, равна нулю II закон: Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение. F = ma Комментарии: F – это равнодействующая сил, приложенных к телу III закон: Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению F1 = - F2 Комментарии: силы всегда встречаются парами

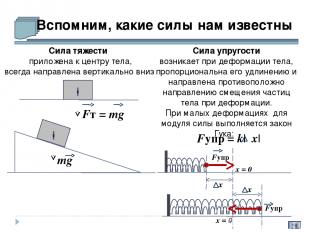
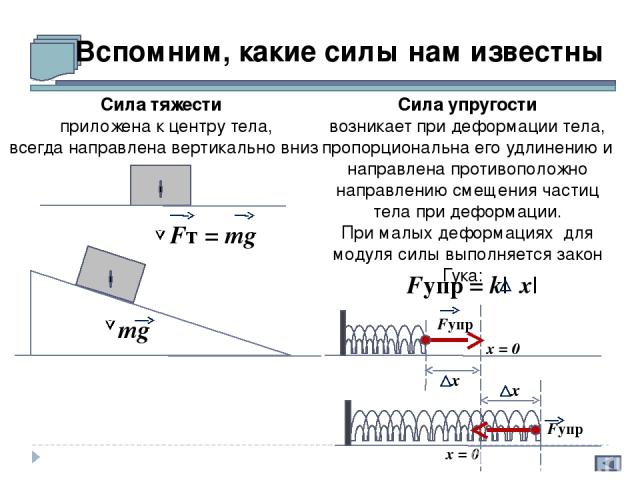
Вспомним, какие силы нам известны Сила тяжести приложена к центру тела, всегда направлена вертикально вниз Fт = mg Сила упругости возникает при деформации тела, пропорциональна его удлинению и направлена противоположно направлению смещения частиц тела при деформации. При малых деформациях для модуля силы выполняется закон Гука: mg Fупр = k| x| x = 0 Fупр x x = 0 x Fупр

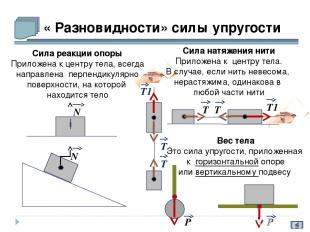
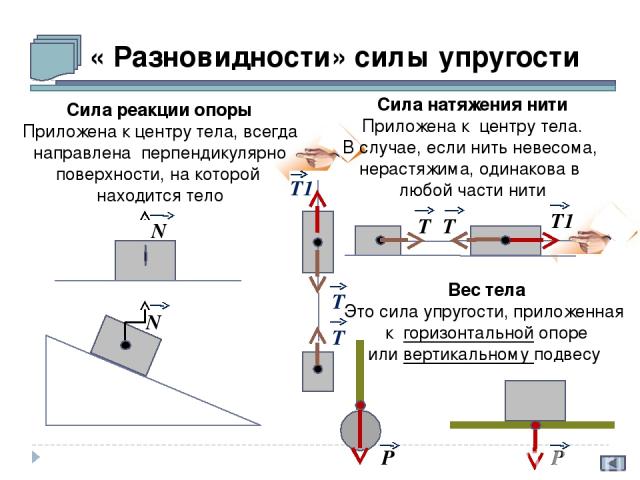
« Разновидности» силы упругости N Т N Т Т1 Сила натяжения нити Приложена к центру тела. В случае, если нить невесома, нерастяжима, одинакова в любой части нити Вес тела Это сила упругости, приложенная к горизонтальной опоре или вертикальному подвесу P P Сила реакции опоры Приложена к центру тела, всегда направлена перпендикулярно поверхности, на которой находится тело Т Т Т1

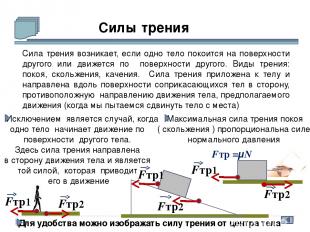
Силы трения Сила трения возникает, если одно тело покоится на поверхности другого или движется по поверхности другого. Виды трения: покоя, скольжения, качения. Сила трения приложена к телу и направлена вдоль поверхности соприкасающихся тел в сторону, противоположную направлению движения тела, предполагаемого движения (когда мы пытаемся сдвинуть тело с места) Исключением является случай, когда одно тело начинает движение по поверхности другого тела. Здесь сила трения направлена в сторону движения тела и является той силой, которая приводит его в движение Fтр1 Fтр2 Максимальная сила трения покоя ( скольжения ) пропорциональна силе нормального давления Fтр1 Fтр2 Fтр1 Fтр2 Для удобства можно изображать силу трения от центра тела Fтр = μN

m1g Два тела массами 50 г и 100 г связаны нитью и лежат на гладкой горизонтальной поверхности. С какой силой можно тянуть первое тело, чтобы нить, выдерживающая максимальную силу натяжения 5 Н, не оборвалась? Дано: m1= 50 г = 0,05 кг m2= 100 г = 0,1 кг F - ? Т = 5 Н N1 F N2 Т Т m2g Решение: Х У а m1a = m1g + Т + N1 + F m2a = m2g + Т + N2 1 2 3 m1a = – Т + F (1) Ох : m2a = Т (2) 4 Выражая из (2) : а = Т/m2 , и подставляя в (1), получим m1 Т/m2 = – T + F F = m1 T/m2 + Т 5 F = 0,05 кг . 5Н/ 0,1 кг + 5 Н = 7,5 Н Ответ: F= 7,5 Н

Автодрезина ведет равноускоренно две платформы массами 12 т и 8 т. Сила тяги, развиваемая дрезиной , равна 1,78 кН. Коэффициент трения равен 0,06. С какой слой натянута сцепка между платформами? Дано: m1= 12 т = 12 000 кг m2= 8 т = 8 000 кг F = 1,78 кН = 1780 Н μ = 0,06 Т - ? 1 Решение: m1g N1 F N2 Т Т m2g Х У а Fтр2 Fтр1 2 m1a = m1g + Т+ N1+ F +Fтр1 m2a = m2g + Т + N2 +Fтр2 3 Ох: m1a = - Т+ F - Fтр1 (1) m2a = Т - Fтр2 (2) Оу: 0 = -m1g + N1, откуда N1 = m1g (3) 0 = -m2g + N2 , откуда N2 = m2g (4) Fтр1 = μ N1= μ m1g , Fтр2 = μ N2 = μ m2 g 4 m1a = -Т+ F - μ m1g (5) m2 a = Т - μ m2 g , a = Т - μ m2 g m2 С учетом (3) и (4) для сил трения имеем: Подставив эти выражения в (1) и (2), получим: После подстановки (6) в (5) остается выразить Т: (6) Т = m2F / (m1 + m2) = 712 Н Ответ: Т = 712 Н

Тело массой 50 кг придавлено к вертикальной стене силой 4 Н. Какая сила необходима для того, чтобы перемещать его вертикально вверх с ускорением 0,2 м/с2, если коэффициент трения 0,5 ? μ = 0,5 а = 0,2 м/с2 F - ? Дано: m = 50 кг Fдав = 4 Н Решение: 1 У 0 F Fдав mg N а Fтр ma = mg + Fдав + N + F + Fтр 2 Х 3 Оy: ma = - mg - Fтр + F (1) Оx: 0 = – Fдав + N (2) 4 Из (2): N = Fдав Имеем, Fтр = μ N = μ Fдав Подставим это выражение в (1) : ma = - mg - μ Fдав + F F = mg + μ Fдав + ma F = m (а + g) + μ Fдав 5 F = 50 кг (0,2 м/с2 + 9,8 м/с2) + 0,5 . 4 Н = 502 Н. Ответ: F = 502 Н

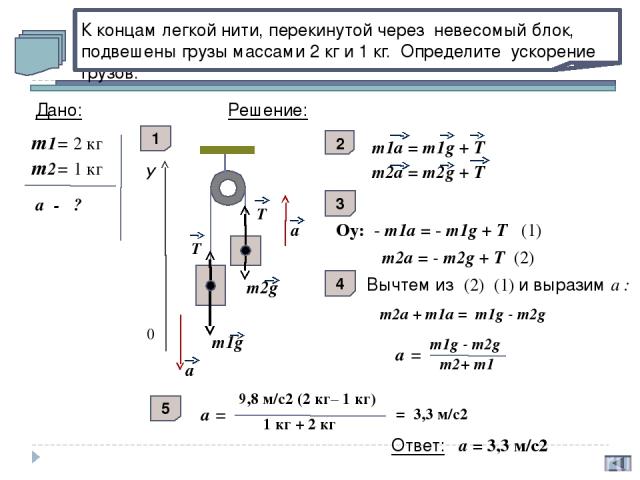
К концам легкой нити, перекинутой через невесомый блок, подвешены грузы массами 2 кг и 1 кг. Определите ускорение грузов. T Дано: m1= 2 кг m2= 1 кг а - ? У 0 m2g m1g T а а Решение: 1 m1a = m1g + Т m2a = m2g + Т 2 Оy: - m1a = - m1g + Т (1) 3 m2a = - m2g + Т (2) 4 Вычтем из (2) (1) и выразим а : m2a + m1a = m1g - m2g a = m1g - m2g m2+ m1 5 a = 9,8 м/с2 (2 кг– 1 кг) 1 кг + 2 кг = 3,3 м/с2 Ответ: а = 3,3 м/с2

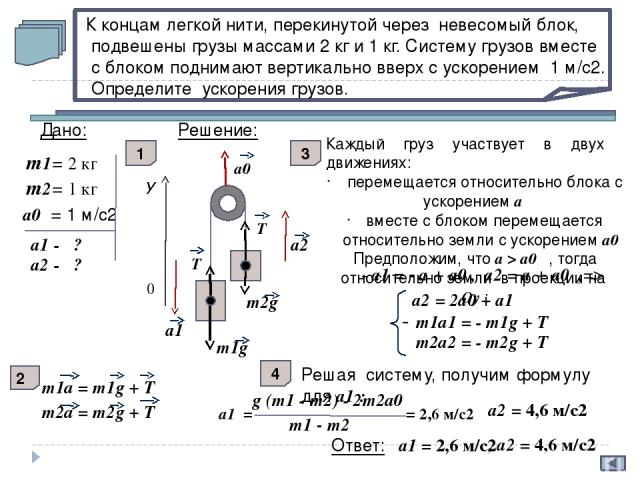
T К концам легкой нити, перекинутой через невесомый блок, подвешены грузы массами 2 кг и 1 кг. Систему грузов вместе с блоком поднимают вертикально вверх с ускорением 1 м/с2. Определите ускорения грузов. Дано: m1= 2 кг m2= 1 кг а0 = 1 м/с2 а1 - ? а2 - ? У 0 m2g m1g T а1 а2 Решение: 1 а0 Каждый груз участвует в двух движениях: перемещается относительно блока с ускорением а вместе с блоком перемещается относительно земли с ускорением а0 Предположим, что а > а0 , тогда относительно земли в проекции на Оу : 2 - а1 = - а + а0 , а2 = а + а0 ,=> m1a = m1g + Т m2a = m2g + Т а2 = 2а0 + а1 - m1a1 = - m1g + Т m2a2 = - m2g + Т 3 4 Решая систему, получим формулу для а1 : а1 = g (m1 - m2) - 2m2a0 m1 - m2 = 2,6 м/с2 а2 = 4,6 м/с2 Ответ: а1 = 2,6 м/с2 , а2 = 4,6 м/с2

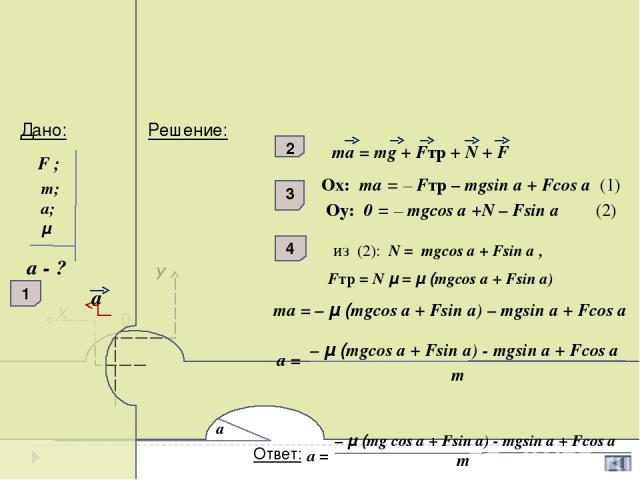
На брусок массой m действует горизонтальная сила F, параллельная основанию наклонной плоскости с углом при основании a. С каким ускорением движется брусок к вершине, если коэффициент трения μ ? mg N F Fтр. а У Х 0 а Дано: Решение: F ; m; a; μ а - ? ma = mg + Fтр + N + F 1 2 3 Оx: ma = – Fтр – mgsin а + Fcos а (1) Оy: 0 = – mgcos а +N – Fsin а (2) 4 из (2): N = mgcos а + Fsin а , Fтр = N μ = μ (mgcos а + Fsin а) ma = – μ (mgcos а + Fsin а) – mgsin а + Fcos а – μ (mgcos а + Fsin а) - mgsin а + Fcos а m Ответ: – μ (mg cos а + Fsin а) - mgsin а + Fcos а a = m a =

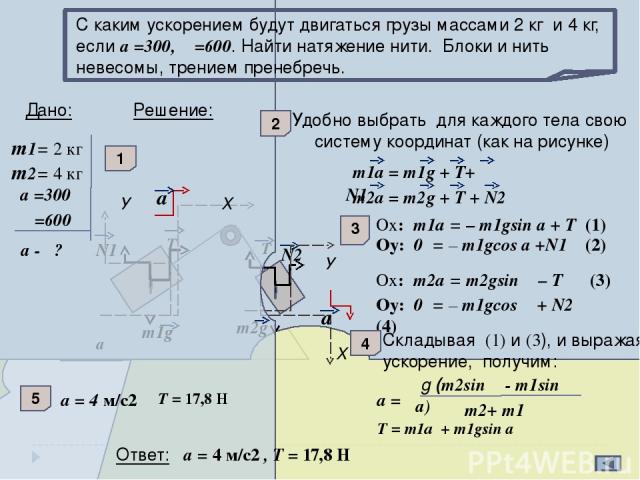
а β m1g m2g N1 N2 T T У У Х Х а а С каким ускорением будут двигаться грузы массами 2 кг и 4 кг, если а =300, β =600. Найти натяжение нити. Блоки и нить невесомы, трением пренебречь. m1= 2 кг m2= 4 кг Дано: а =300 β =600 а - ? Решение: 1 2 Удобно выбрать для каждого тела свою систему координат (как на рисунке) m1a = m1g + Т+ N1 m2a = m2g + Т + N2 3 Оx: m1a = – m1gsin а + Т (1) Оy: 0 = – m1gcos а +N1 (2) Оx: m2a = m2gsin β – Т (3) Оy: 0 = – m1gcos β + N2 (4) 4 Складывая (1) и (3), и выражая ускорение, получим: g (m2sin β - m1sin а) a = m2+ m1 Т = 17,8 H T = m1a + m1gsin а 5 a = 4 м/с2 Ответ: а = 4 м/с2 , T = 17,8 H

Шары массами m1 ,m2 ,m3 подвешены к потолку с помощью двух невесомых пружин и легкой нити. Система покоится. Определите силу натяжения нити . Определите направление и модуль ускорения шара массой m1 сразу после пережигания нити. m1g T T m2g Fупр1. Fупр2. Fупр2. m3g m1; m2 ; m3 ; а-? T-? Дано: Решение: У 0 а 1. Для ясности можно провести «мысленный эксперимент» – представить, что в середине нити находится динамометр. Получается , что к нему прикрепили грузы массами m2 и m3. Естественно, его показания будут равны: Т = g (m2 + m3 ) 2. В момент пережигания нити на верхний шар действуют только две силы : Fупр1. и m1g , которые и сообщают шару ускорение. m1a = m1g +Fупр1 Fупр1 = g (m1 + m 2 + m3 ) ( см. п.1 ) a = g (m2 + m3 ) / m1 Окончательно после преобразований получим:

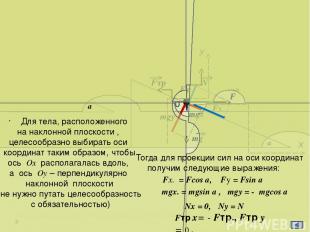
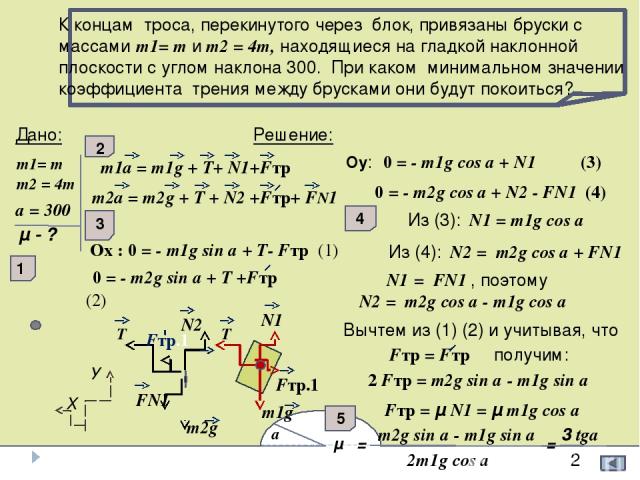
а Х FN1 N2 m1g m2g T 1 У T Fтр.1 N1 К концам троса, перекинутого через блок, привязаны бруски с массами m1= m и m2 = 4m, находящиеся на гладкой наклонной плоскости с углом наклона 300. При каком минимальном значении коэффициента трения между брусками они будут покоиться? m1= m m2 = 4m а = 300 μ - ? Дано: Решение: m1a = m1g + Т+ N1+Fтр m2a = m2g + Т + N2 +Fтр+ FN1 Ох : 0 = - m1g sin а + Т- Fтр (1) 0 = - m2g sin а + Т +Fтр (2) Оу: 0 = - m1g cos а + N1 (3) 0 = - m2g cos а + N2 - FN1 (4) Из (3): N1 = m1g cos а Из (4): N2 = m2g cos а + FN1 N1 = FN1 , поэтому N2 = m2g cos а - m1g cos а Вычтем из (1) (2) и учитывая, что Fтр = Fтр получим: 2 2 Fтр = m2g sin а - m1g sin а Fтр = μ N1 = μ m1g cos а μ = m2g sin а - m1g sin а 2m1g cos а 3 tgа = 2 3 4 5 Fтр.1

Список литературы Г. Я. Мякишев. Физика: Учебник для 10 кл. общеобразовательных учреждений / Г. Я. Мякишев, Б. Б. Буховцев, Н. Н.Сотский. – М. : Просвещение, 2008. Кирик Л. А. Физика – 9. Разноуровненые самостоятельные и контрольные работы. – М.: Илекса, 2003. Задачи вступительных экзаменов в МФТИ .