Презентация на тему: уравнение максвелла

Уравнения Максвелла для электромагнитного поля 1. Аналогия между характеристиками электрического и магнитного полей:

Первое уравнение Максвелла представляет собой закон полного тока: Смысл первого уравнения Максвелла состоит в том, что любой ток проводимости I порождает вихревое магнитное поле , циркуляция которого вдоль произ-вольного замкнутого контура l равна I. Одновременно, всякое изменение вектора электрического смещения также как и ток проводимости, порождает вихревое магнитное поле .

Второе уравнение Максвелла представляет собой закон электромагнитной индукции. Максвелл высказал гипотезу, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводящем контуре. Иначе « изменяющееся во времени магнитное поле порождает вихревое электрическое поле , циркуляция которого вдоль произвольного замкнутого контура l равна

Третье и четвертое уравнения Максвелла Третье уравнений Максвелла в интегральной форме выражает тот факт, что в природе отсутствуют магнитные заряды, т.е. все силовые линии вектора являются замкнутыми линиями. Суть четвертого уравнения состоит в том, что поток вектора электрического смещения через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов ΣQ, расположенных внутри этой поверхности.

Полная система уравнений Максвелла в дифференциальной форме Полная система уравнений Максвелла в дифференциальной форме Отметим, что в уравнениях Максвелла (1873 г.) заложено существование электромагнитных волн. Согласно уравнениям Максвелла, всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, а всякое переменное электрическое поле вызывает появление вихревого магнитного поля. Возбуждение взаимосвязанных электрического и магнитного полей и есть электромагнитная волна. Экспериментальное подтверждение гениальных предсказаний Максвелла было осуществлено в опытах Герца в 1888 г.
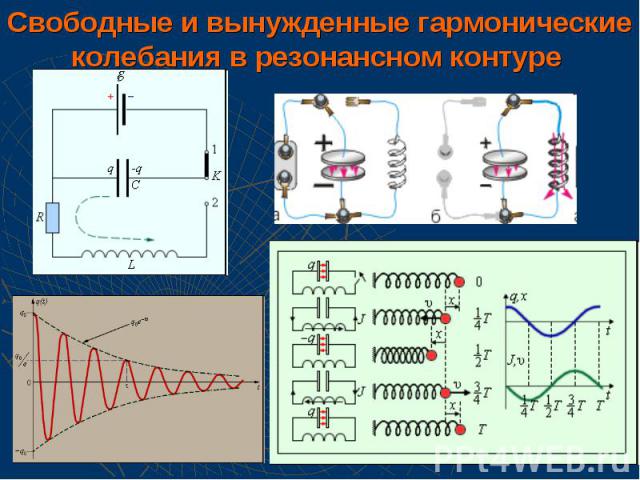
Свободные и вынужденные гармонические колебания в резонансном контуре

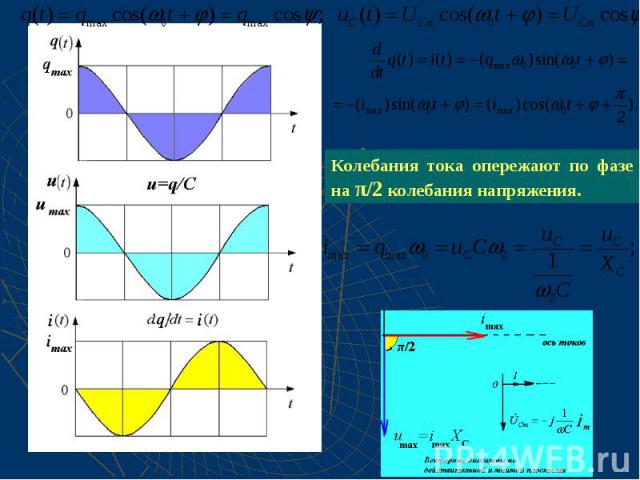
II Закон Кирхгофа для замкнутой RLC-цепи: II Закон Кирхгофа для замкнутой RLC-цепи: Рассмотрим сначала случай, когда в контуре нет потерь (R = 0). Тогда
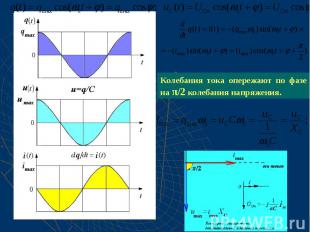

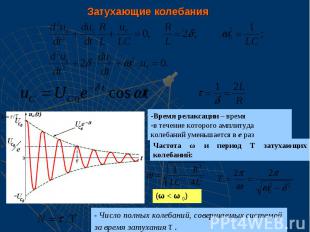
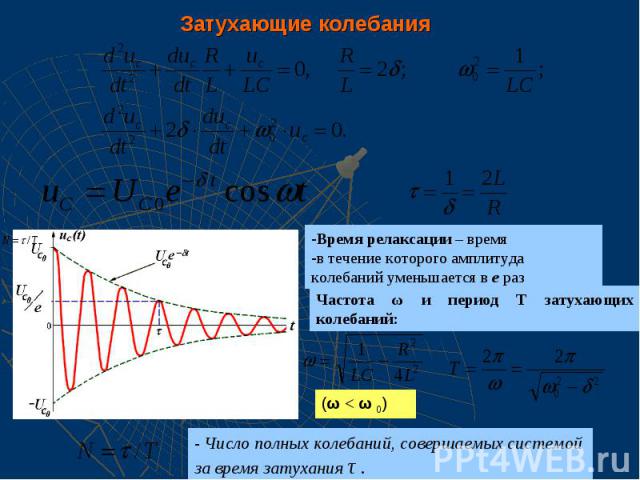
Затухающие колебания
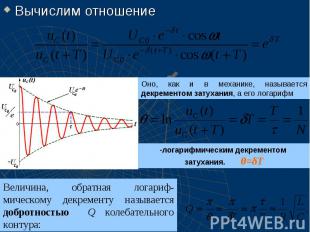
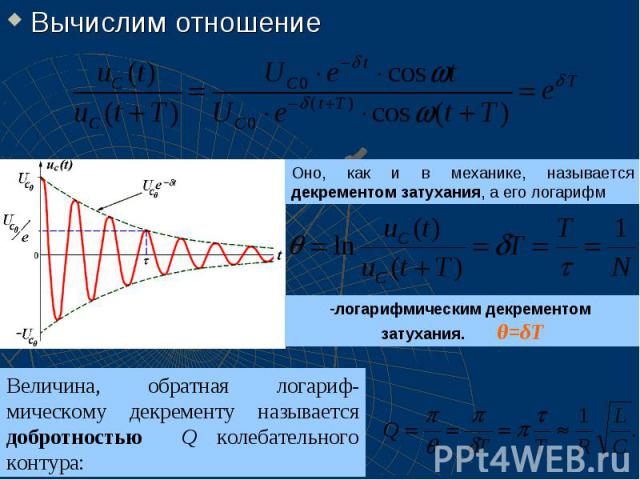
Вычислим отношение Вычислим отношение

Вынужденные колебания в RLC контуре


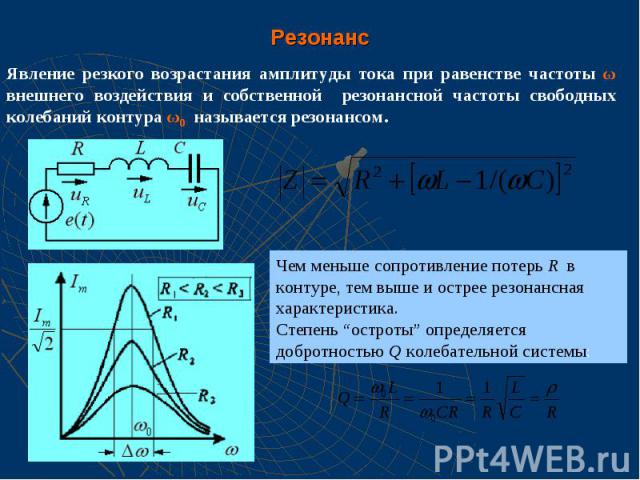
Резонанс

Мощность в цепи переменного тока