Презентация на тему: Применение пакета RMD для изучения движения материальных тел

Отчет о НИР «О возможности применения пакета RMD для изучения движения материальных тел» Выполнил: студент кафедры РВКС – Максимилиан Тютькин В ночь до выступления отчет был послан научному руководителю: проф. Сениченкову Ю.Б.

Неформальное описание проблемы Великий Аристотель утверждает [1], что «для движения нужен движитель». Трудно возразить великому физику, так как повседневный опыт подтверждает его гениальный закон: действительно, может ли телега сама доехать до дома? И опыт, и Аристотель говорят, что скорость движения пропорциональна приложенной силе – опять же все мы знаем: «Баба с возу - кобыле легче». Однако при внимательном рассмотрении, оказывается, что теория Аристотеля не до конца объясняет некоторые явления. Камень, брошенный бестолковой бабой в мужа, По Аристотелю должен немедленно остановиться, как только она выпустит камень из руки, не причинив вреда мужу, ан нет – синяк налицо! Действительно:

Формализация задачи и контрпример. Великий ученый Галилео Галилей [2] говорит: «Если закон Аристотеля записать в форме где -сила, - вектор скорости, - коэффициент пропорциональности, и применить его к камню, движущемуся в некоторой системе координат, то станет очевидным, что как только сила становится равной нулю, скорость тоже становится нулевой. Но опыт говорит, что тела еще некоторое время продолжают двигаться, после того как непосредственное воздействие на них прекращается….» Следовательно должна существовать еще какая-то неравномерная, постепенно уменьшающаяся и неведомая нам сила! Я проконсультировался с батюшкой, преподающего закон Божий в нашем университете, и он сказал, что неведомых сил не бывает, на все воля Божья!

Галилеевы или инерциальные системы отсчета Галилей построил еще один пример: Пусть та же баба толкает тележку по берегу моря со скоростью Эту картину одновременно наблюдают двое: один на берегу, а второй – на корабле, двигающемся относительно берега с постоянной скоростью . Наблюдатель, измерив скорость тележки с корабля, установит, что она равна . Следовательно в подвижной системе координат к тележке приложена сила , a в неподвижной - Тут уж любой сообразит, что дело неладно: сил две, а баба – одна!

Уравнения Ньютона Устранить это противоречие предложил английский ученый I. Newton [] или ISAKO NEWTONO [3], что по-русски, наверное, будет звучать так: Исаак Ньютон. Он заменил закон движения в форме Аристотеля, на новый Последнее дифференциальное уравнение второго порядка, при равной нулю силе, имеет решение , что делает системы отсчета из предыдущего примера равноправными, а основной формой движения не покой, равномерное движение.

Постановка задачи Как справедливо отмечает заведующий нашей кафедры Ю.Г. Карпов в своей книге «Имитационное моделирование», компьютерное моделирование: 1) дает возможность глубже понять явления и предсказать поведение объектов, 2) позволяет избежать рутинных расчетов, особенно если вам доступны такие инструменты как AnyLogic [4] и Rand Model Designer [5], созданные сотрудниками и выпускниками нашей кафедры, 3) снизить материальные затраты на проведение многочисленных дорогостоящих экспериментов, заменив их вычислительными. Когда гипотеза будет подтверждена для виртуальных объектов, достаточно провести один контрольный натурный эксперимент! Попробуем провести этот виртуальный эксперимент и подтвердить гипотезу Ньютона.

В качестве изучаемого явления выберем полет тела в поле тяжести Земли, брошенного под углом к горизонту. Математическая модель содержит два обыкновенных дифференциальных уравнения второго порядка и очень сложна для ручного расчета! При применении современных инструментов моделирования*) для получения правильного решения достаточно только описать модель! (я хотел выбрать пакет AnyLogic, рекомендованный в книге профессора Ю.Г. Карпова, но профессор Ю.Б. Сениченков настоял на применении пакета RMD, мотивируя это тем, что математические модели на языке MVL сохраняют привычную математическую нотацию, в то время как в AnyLogic используется «алгоритмическая нотация» – правую часть уравнения нужно писать в виде процедуры-функции на языке низкого уровня),

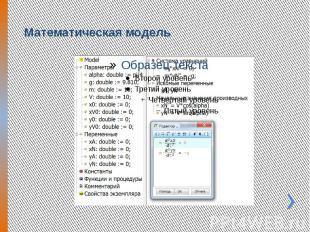
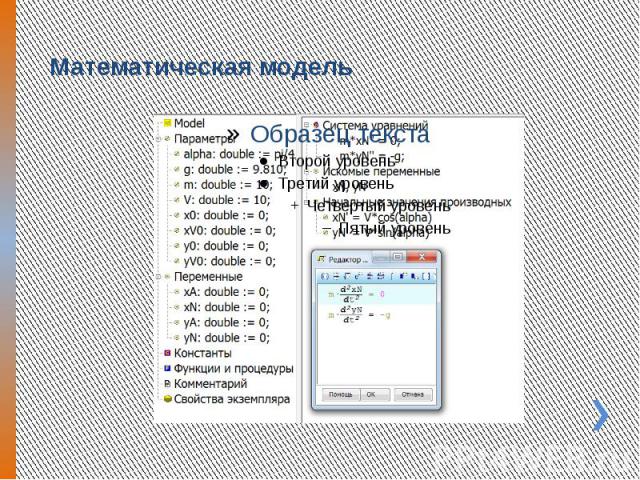
Математическая модель

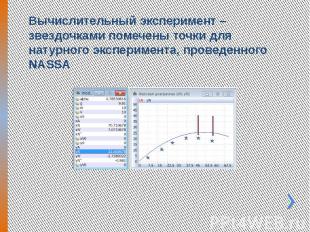
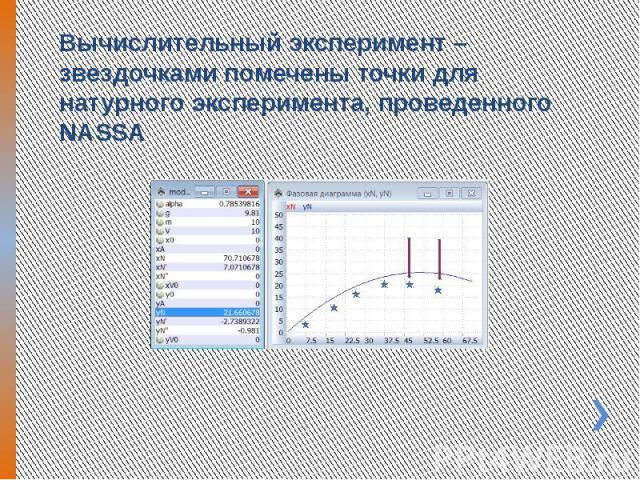
Вычислительный эксперимент – звездочками помечены точки для натурного эксперимента, проведенного NASSA

Сравнение результатов натурного и вычислительного эксперимента Как уже отмечалось Галилеем, модель Аристотеля предсказывает мгновенное падение камня ка землю. Ньютоновская модель дает много лучшие результаты, (несомненно достоверные качественно), а полученные отличия в предсказании времени и места падения объясняются наличием не учтенных сил трения. чем я и буду заниматься в следующем семестре.

Гипотеза о силе Божьей Математическое моделирование позволяет проверить и гипотезу о силе Божьей. Батюшка, читающий Закон Божий, порекомендовал мне сравнить две возможные силы: пропорциональные 1) убывающей экспоненте и 2) линейной функции от времени. Опираясь на данные реального полета, я подобрал коэффициенты функций, обеспечивающие падение шарика в замеренной точке.

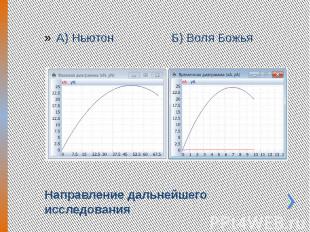
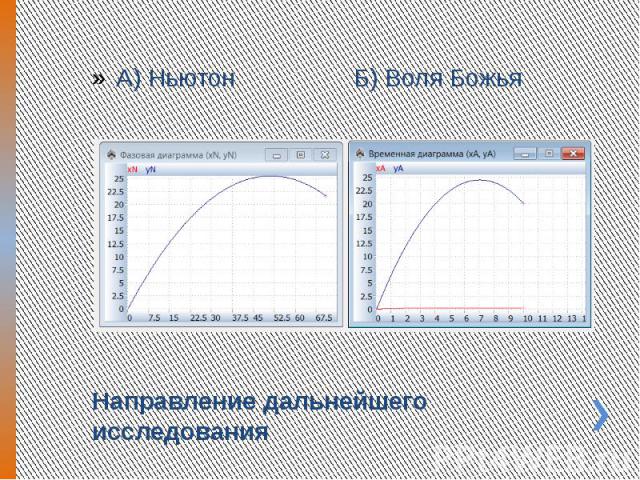
Направление дальнейшего исследования А) Ньютон Б) Воля Божья

Список литературы 1. из книги "ФИЛОСОФЫ ГРЕЦИИ ОСНОВЫ ОСНОВ: ЛОГИКА, ФИЗИКА, ЭТИКА" издательство ЭКСМО-Пресс; Харьков 1999, 1056 с. Перевод: В.П.Карпов 2. Ньютон Исаaк. Математические начала натуральной философии: Пер. с лат./Под ред. и с предисл. Л.С. Полака. Изд. 3-е – М: Издательство ЛКИ, 2008.- 704 с. 3. Краснощеков П.С., Петров А.А. Принципы построения моделей - М: Издательство МГУ, 1983.- 264 с. 4. www.AnyLogic.com 5. www.mvstudium.com

СПАСИБО!