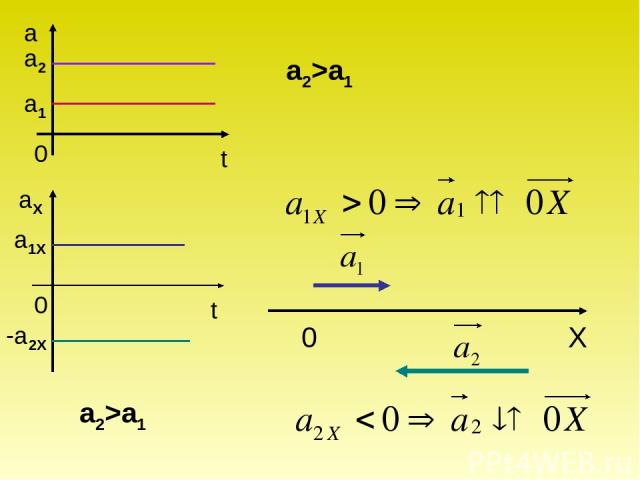Презентация на тему: Мгновенная скорость

Мгновенная скорость 900igr.net

Чтобы определить мгновенную скорость нужно: 1. Измерить среднюю скорость за интервал времени от t до t+∆t 2. Принять, что средняя скорость за этот промежуток примерно равна скорости в момент времени t. Чем меньше промежуток времени, тем точнее определена скорость. (∆t→0) Скорость тела в данной точке траектории в данный момент времени называется мгновенной скоростью.

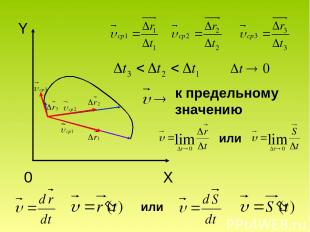
к предельному значению или или

Частный случай- равномерное прямолинейное движение: направление скорости совпадает с траекторией в направлении вектора перемещения. Мгновенной скоростью называется предел отношения перемещения к интервалу времени, в течение которого это перемещение произошло, если интервал времени стремится к нулю.

Проекции вектора скорости на координатные оси. Модуль вектора скорости

Ускорение Ускорение это величина, характеризующая быстроту изменения скорости.

A1 A2

или

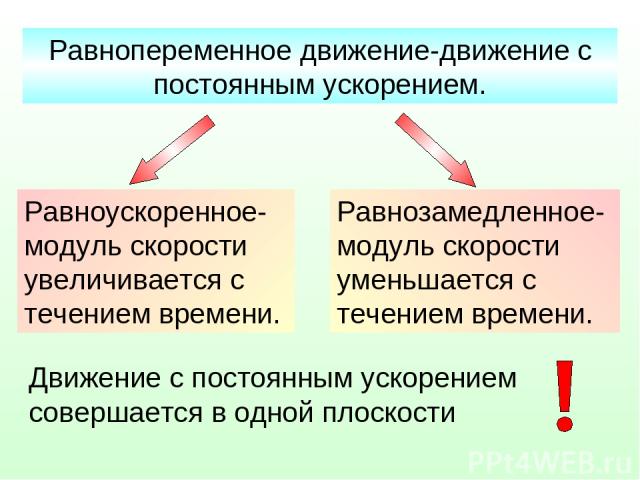
Равнопеременное движение-движение с постоянным ускорением. Равноускоренное- модуль скорости увеличивается с течением времени. Равнозамедленное- модуль скорости уменьшается с течением времени. Движение с постоянным ускорением совершается в одной плоскости

модуль вектора скорости

Скорость при равнопеременном движении Вектор мгновенной скорости Векторное уравнение при движении на плоскости эквивалентно двум уравнениям для проекций вектора на координатные оси

Графическое представление равнопеременного движения Графики модуля и проекции ускорения

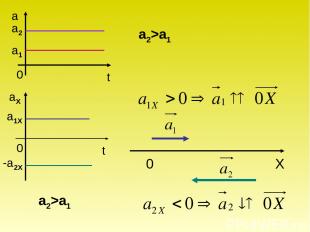
a1X -a2X a2 a1 a2>a1 a2>a1

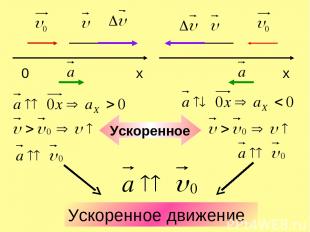
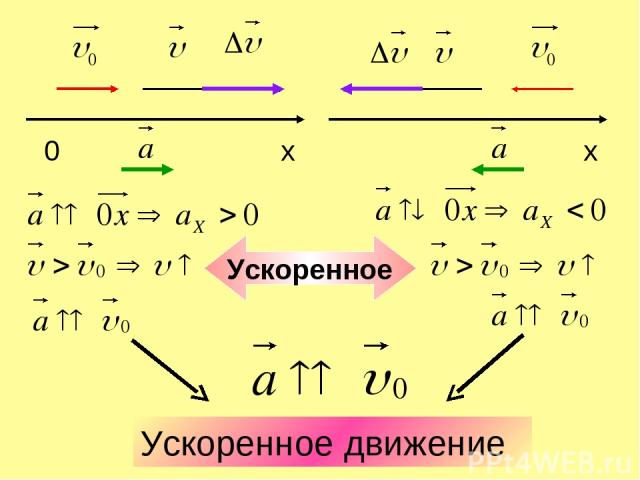
Ускоренное движение Ускоренное

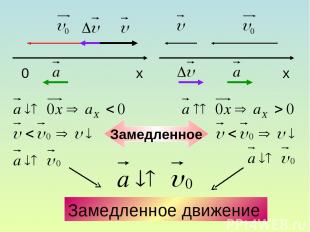
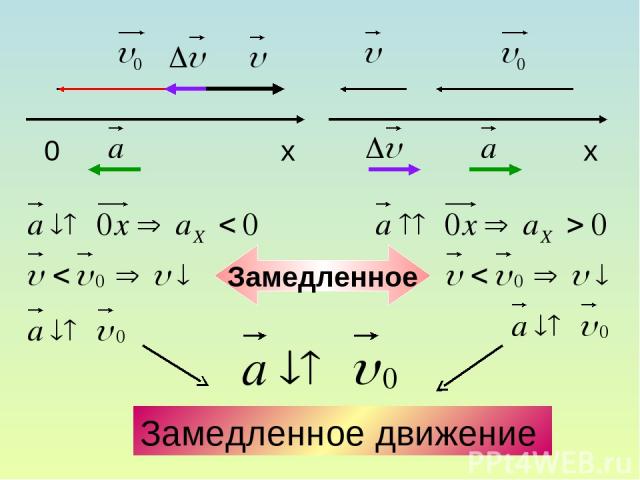
Замедленное движение Замедленное

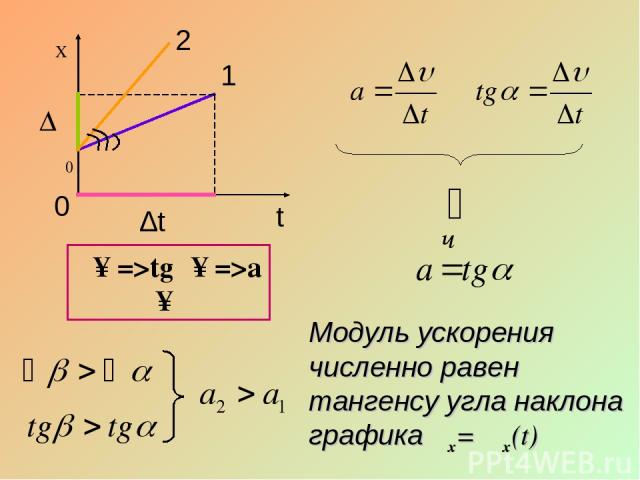
График зависимости проекции скорости от времени υX= υX(t)

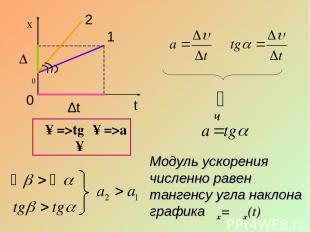
υ α 1 υ0 ∆t ∆υ Модуль ускорения численно равен тангенсу угла наклона графика υx= υ x(t) α↑=>tgα↑=>a↑ β 2

1 ∆υ1x 2 α ∆υ1x β 1-е тело υ↑ 2-е тело υ↑

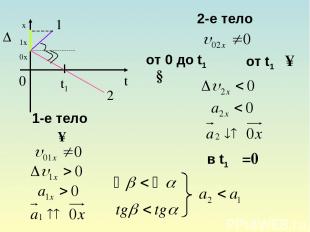
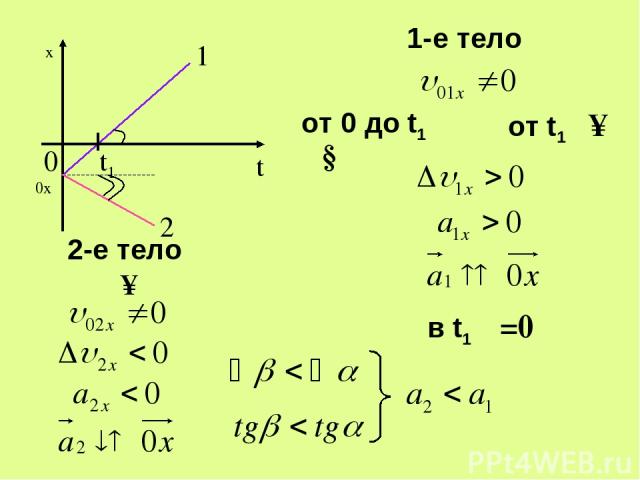
1 ∆υ1x α υ0x 2 t1 β 1-е тело υ↑ 2-е тело от 0 до t1 υ↓ от t1 υ↑ в t1 υ=0

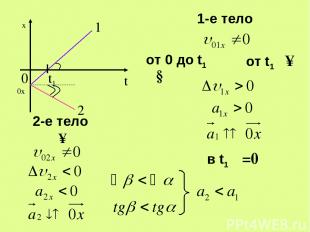
1 α υ0x 2 t1 β 2-е тело υ↑ 1-е тело от 0 до t1 υ↓ от t1 υ↑ в t1 υ=0 0

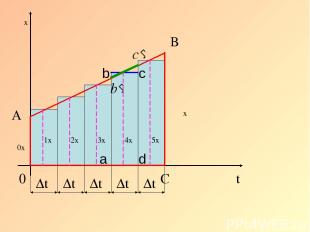
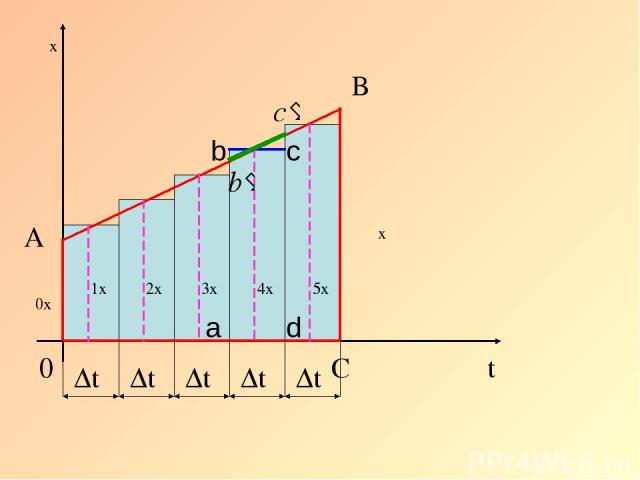
υ0x υx C B A υ1x υ4x υ2x υ3x υ5x b c a d

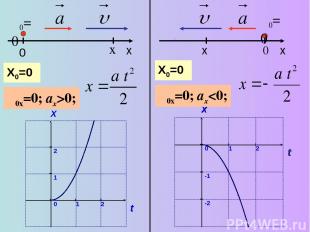
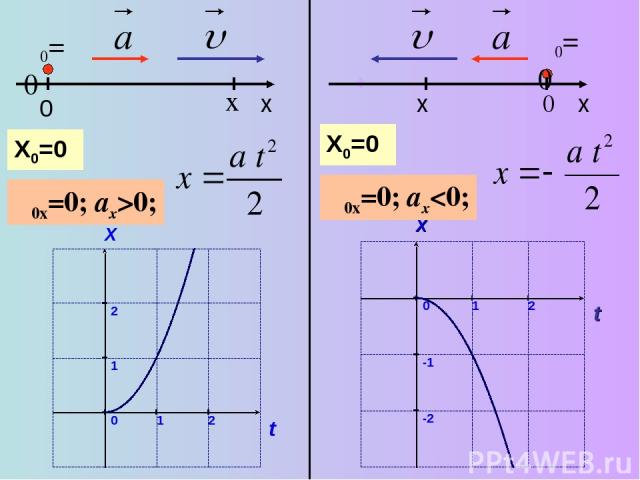
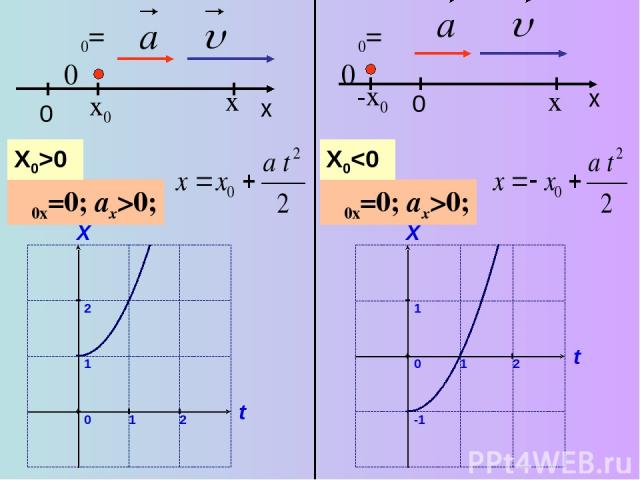
υ0=0 x υ0x=0; ax>0; υ0=0 0 υ0x=0; ax

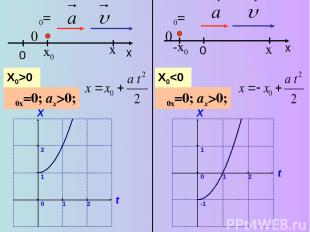
υ0=0 x υ0x=0; ax>0; x0 X0>0 0 x υ0=0 x υ0x=0; ax>0; -x0 X0

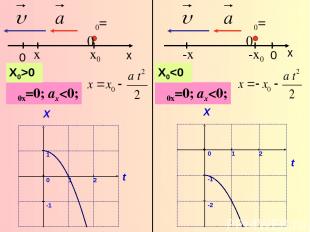
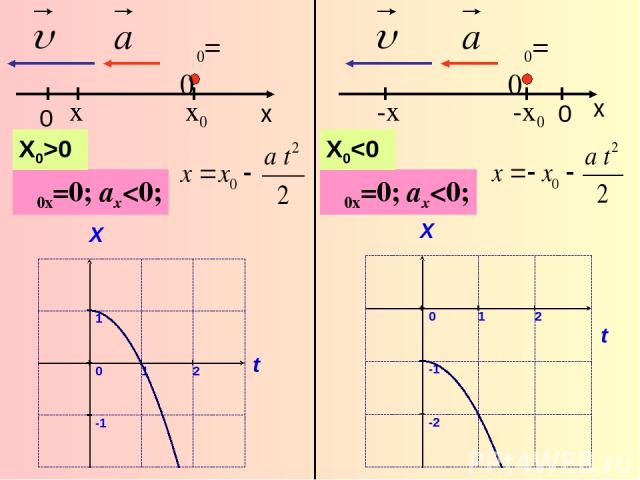
υ0=0 x υ0x=0; ax0 0 x υ0=0 -x υ0x=0; ax

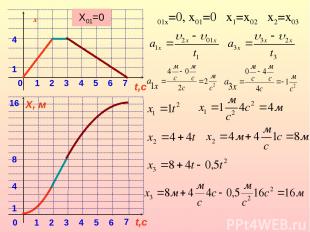
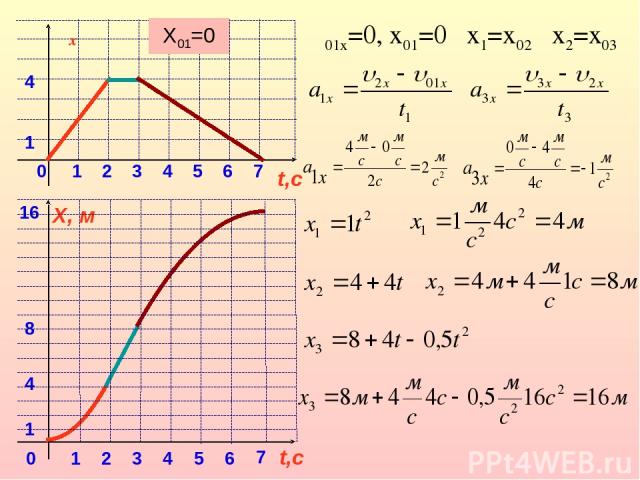
16 8 4 1 0 t,с X, м 1 2 3 4 5 6 7 4 1 0 t,с υx 1 2 3 4 5 6 7 υ01x=0, x01=0 X01=0 x1=x02 x2=x03

Работу выполнили: Игошин Александр Владимирович Алейникова Татьяна Владимировна