Презентация на тему: Первая космическая скорость. Вес и невесомость

Глава 4. Силы в механике первая космическая скоростФизика, 10 класс ь. Вес и Невесомость Рахматуллин Радик Акрамович, учитель физики МОУ «Александровская СОШ», 2010

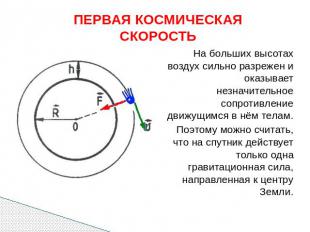
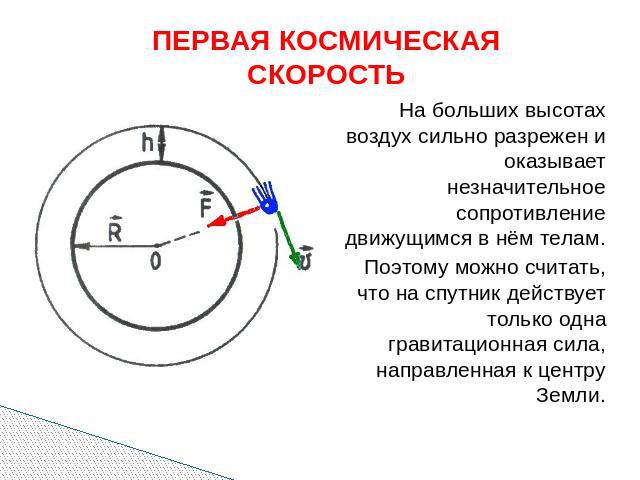
ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ На больших высотах воздух сильно разрежен и оказывает незначительное сопротивление движущимся в нём телам. Поэтому можно считать, что на спутник действует только одна гравитационная сила, направленная к центру Земли.

Из полученной формулы следует, что скорость спутника зависит от его высоты над поверхностью Земли: чем больше эта высота, тем с меньшей скоростью он будет двигаться по круговой орбите. Примечательно то, что эта скорость не зависит от массы спутника. Значит, спутником Земли может стать любое тело, если ему сообщить определённую скорость. В частности, при h = 2000 км скорость υ ≈ 6900 м/с. Скорость, которую необходимо сообщить телу у поверхности планеты, чтобы оно стало её спутником, движущимся по круговой орбите, называется первой космической скоростью.

Первую космическую скорость υ1 можно найти, если принять h = 0: Подставив в эту формулу значение G и значение величин М и R для Земли, можно вычислить первую космическую скорость для спутника Земли:

Если такую скорость сообщить телу в горизонтальном направлении у поверхности Земли, то при отсутствии атмосферы оно станет искусственным спутником Земли, обращающимся вокруг неё по круговой орбите Такую скорость спутникам способны сообщать только мощные космические ракеты.

В настоящее время вокруг Земли обращаются тысячи искусственных спутников. Руками человека за годы освоения космоса создавались и искусственные спутники Луны, планет Венера и Марс, а также Солнца.

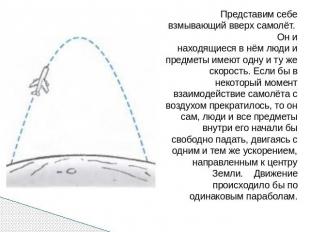
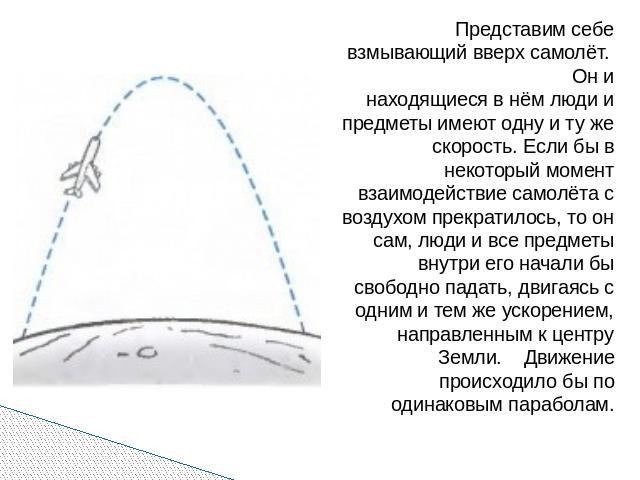
Представим себе взмывающий вверх самолёт. Он и находящиеся в нём люди и предметы имеют одну и ту же скорость. Если бы в некоторый момент взаимодействие самолёта с воздухом прекратилось, то он сам, люди и все предметы внутри его начали бы свободно падать, двигаясь с одним и тем же ускорением, направленным к центру Земли. Движение происходило бы по одинаковым параболам.

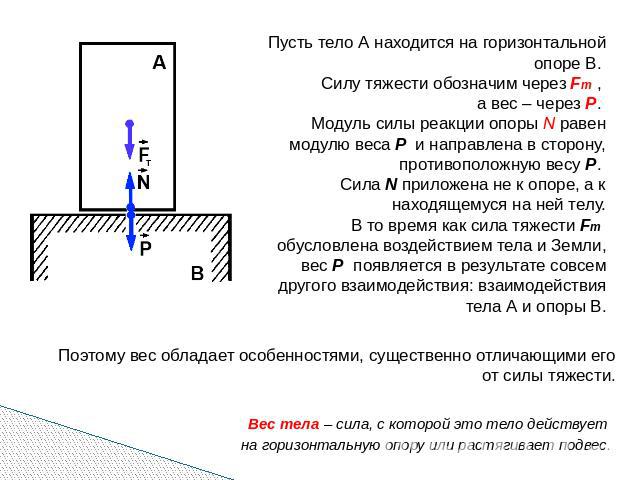
Пусть тело А находится на горизонтальной опоре В. Силу тяжести обозначим через Fт , а вес – через Р. Модуль силы реакции опоры N равен модулю веса Р и направлена в сторону, противоположную весу Р. Сила N приложена не к опоре, а к находящемуся на ней телу. В то время как сила тяжести Fт обусловлена воздействием тела и Земли, вес Р появляется в результате совсем другого взаимодействия: взаимодействия тела А и опоры В. Поэтому вес обладает особенностями, существенно отличающими его от силы тяжести. Вес тела – сила, с которой это тело действует на горизонтальную опору или растягивает подвес.

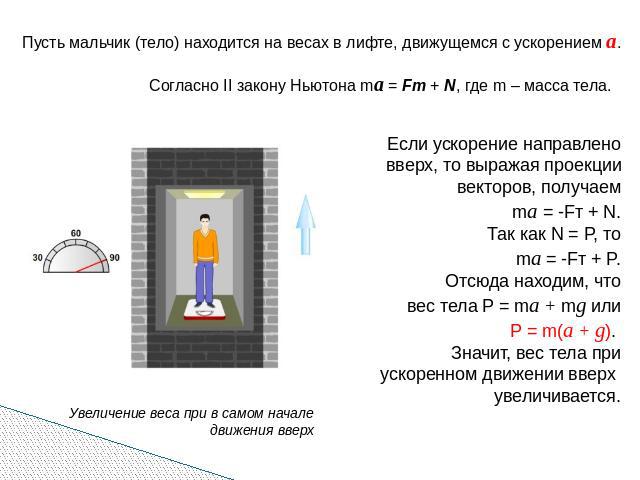
Пусть мальчик (тело) находится на весах в лифте, движущемся с ускорением а. Согласно II закону Ньютона ma = Fт + N, где m – масса тела. Если ускорение направлено вверх, то выражая проекции векторов, получаем ma = -Fт + N. Так как N = P, то ma = -Fт + P. Отсюда находим, что вес тела P = ma + mg или Р = m(a + g). Значит, вес тела при ускоренном движении вверх увеличивается. Увеличение веса при в самом начале движения вверх

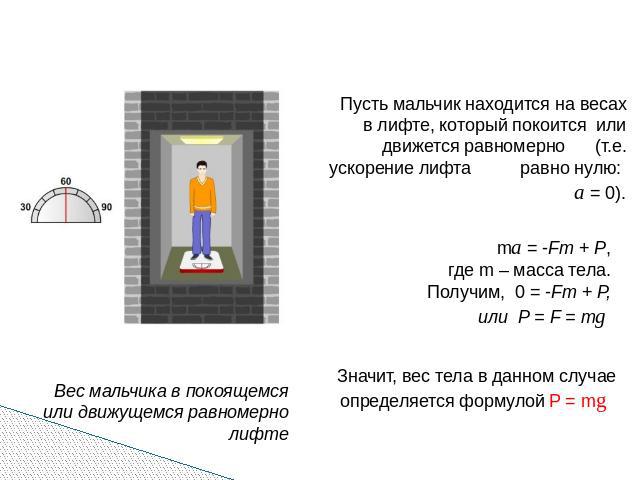
Пусть мальчик находится на весах в лифте, который покоится или движется равномерно (т.е. ускорение лифта равно нулю: а = 0). ma = -Fт + Р, где m – масса тела. Получим, 0 = -Fт + Р, или Р = F = mg Значит, вес тела в данном случае определяется формулой P = mg Вес мальчика в покоящемся или движущемся равномерно лифте

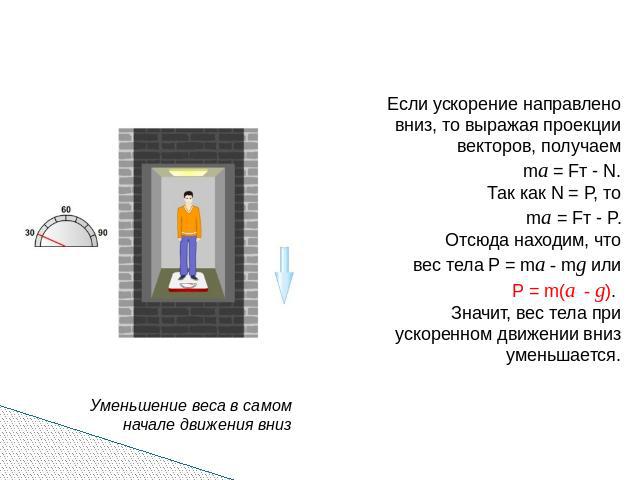
Если ускорение направлено вниз, то выражая проекции векторов, получаем ma = Fт - N. Так как N = P, то ma = Fт - P. Отсюда находим, что вес тела P = ma - mg или Р = m(a - g). Значит, вес тела при ускоренном движении вниз уменьшается. Уменьшение веса в самом начале движения вниз

Спутник падает свободно, т.е. а = g, Тогда вес тел в спутнике (и самого спутника) P = m(g – g) = 0. Вес тела зависит от ускорения, с которым движется опора, и появление этого ускорения эквивалентно изменению ускорения свободного падения. Невесомость в космосе