Презентация на тему: 1 Кинематика

Мирза Мухаммед ибн Шахрух ибн Тимур Улугбек Гураган (1394-1449) -внук Тамерлана. Известен как выдающийся астроном и выполнял работы не имея телескопов. Мирза Мухаммед ибн Шахрух ибн Тимур Улугбек Гураган (1394-1449) -внук Тамерлана. Известен как выдающийся астроном и выполнял работы не имея телескопов. В 17 веке итальянец Г.Галилей (Galileo Galilei, 1564-1642, итальянский физик и астроном) показал, что воздействие на данное тело окружающих тел – определяет ускорение а не скорость, а также независимость ускорения свободного падения от скорости и массы (закон равноускоренного падения). Первым использовал телеcкоп для наблюдения планет. Роберт Гук (Robert Hooke, 1635-1703 теплота, упругость, оптика, небесная механика, биология ) в 1666 году опубликовал за 21 год до Ньютона первую работу по тяготению и по словам Сергея Вавилова, который исследовал работы Гука внес неоспоримый вклад. Непосредственное доказал вращение Земли вокруг Солнца Портретов Гука не сохранилось. Высказал идеи о волнообразном распространении света (более или менее одновременно с Гюйгенсом) и интерференцией света, о поперечном характере световых волн . Гуку принадлежит сам термин "клетка" - англ. cell

И.Ньютон (Isaak Newton 1643-1727 правильно произносить коротко ) английский физик, алхимик, директор монетного королевского двора и глава Лондонского Королевском обществе в 1687 г. (со ссылкой на Гука и других ученых) изложил свои закономерности механического движения в математической форме , используемой до сих пор. И.Ньютон (Isaak Newton 1643-1727 правильно произносить коротко ) английский физик, алхимик, директор монетного королевского двора и глава Лондонского Королевском обществе в 1687 г. (со ссылкой на Гука и других ученых) изложил свои закономерности механического движения в математической форме , используемой до сих пор. Ньютон утверждал о независимом и более раннем открытии этой формулы, сделанную им во время чумы, которую однако до открытия Гуком никому не показывал. Имел обширную переписку с Гуком. Яблоня цела ! стоит на берегу реки ??? Ньютоновская (классическая) механика не применима для описания движения атомов, элементарных частиц и молекул, а также частиц двигающихся со скоростями близкими к скорости света в вакууме с~3х108 м/с. Весь вопрос в величине импульса! Большой или маленький?! Посмотрим на трубу Ньютона Крыша одного из Two Twins в 2001 –тоже упала с g

Относительность движения определяется относительностью самого пространства. Нельзя говорить о положении в абсолютном пространстве, независимо от находящихся в нем тел, а лишь о положении относительно каких то тел. Относительность движения определяется относительностью самого пространства. Нельзя говорить о положении в абсолютном пространстве, независимо от находящихся в нем тел, а лишь о положении относительно каких то тел. Мы будем считать что пространство однородно и изотропно (свойства не зависят от направления). Т.е. фактически Эвклидово пространство. Экспериментально на больших масштабах это не доказано.

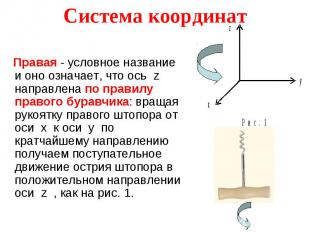
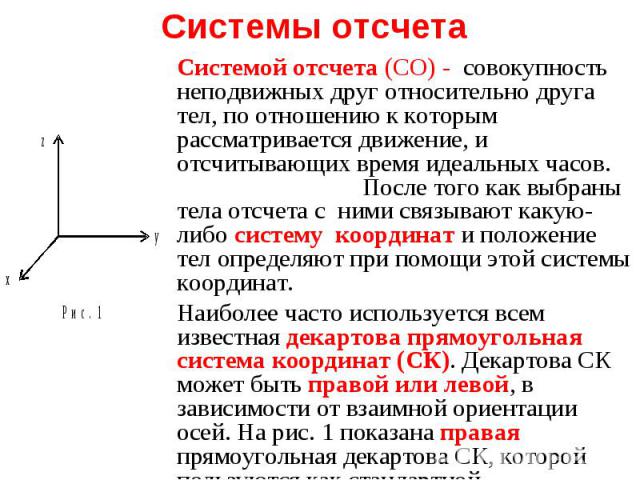
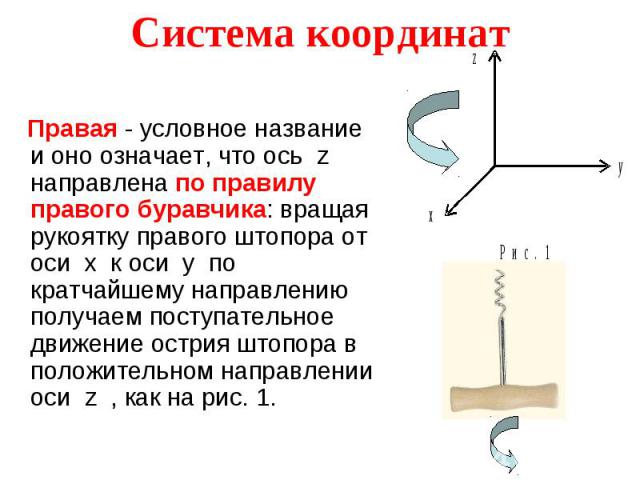
Правая - условное название и оно означает, что ось z направлена по правилу правого буравчика: вращая рукоятку правого штопора от оси x к оси y по кратчайшему направлению получаем поступательное движение острия штопора в положительном направлении оси z , как на рис. 1. Правая - условное название и оно означает, что ось z направлена по правилу правого буравчика: вращая рукоятку правого штопора от оси x к оси y по кратчайшему направлению получаем поступательное движение острия штопора в положительном направлении оси z , как на рис. 1.

Разные СО и СК равны и одинаковы допустимы Разные СО и СК равны и одинаковы допустимы Число СО и СК– бесконечно Надо выбирать СК в которых физические явления и уравнения их описывающие выглядят наиболее просто. Т.е. оси СК надо направлять так, чтобы уравнения описывающие движения выглядели наиболее просто и их было мин. количество. Самый простое- движение по прямой. СК - сама прямая

Материальная точка (МТ)- тело размерами которого (при изучении его движения) можно пренебречь. Это не связано напрямую с его размерами, зависит от условий задачи. Материальная точка (МТ)- тело размерами которого (при изучении его движения) можно пренебречь. Это не связано напрямую с его размерами, зависит от условий задачи. Примеры: Земля движется вокруг Солнца – Земля МТ Суточное вращение Земли вокруг оси – Земля не МТ.

Скаляр - физическая величина, характеризующуюся только одним численным значением. Примером могут быть объем, температура, масса, время и т.д. Скаляр - физическая величина, характеризующуюся только одним численным значением. Примером могут быть объем, температура, масса, время и т.д. Вектора - величины, характеризующиеся численным значением (т.е. некоторым абсолютным значением или модулем) и направлением, и, кроме того, складывающиеся по правилу параллелограмма (бывают величины, изображаемые направленными отрезками, но не складывающиеся по правилу параллелограмма и, следовательно, не являющиеся векторами). Векторами являются, например, скорость, ускорение, сила. На рисунках вектор изображается стрелкой , начало которой находится в точке, где он определен (например, в случае силы F – в точке приложения силы). При любых операциях вектор может переноситься параллельно самому себе. При этом ни его модуль ни ориентация не изменяются.

Численное значение вектора называется его модулем. Мы будем обозначать векторы жирными наклонными буквами: V , a , F. Модуль вектора будем обозначать той же нежирной буквой обычного шрифта V , a , F . В книгах модуль обозначают также символом вектора между двумя вертикальными черточками : Численное значение вектора называется его модулем. Мы будем обозначать векторы жирными наклонными буквами: V , a , F. Модуль вектора будем обозначать той же нежирной буквой обычного шрифта V , a , F . В книгах модуль обозначают также символом вектора между двумя вертикальными черточками : V V, a a, F F.

Векторы могут перемножаться скалярно. Скалярным произведением векторов a и b называется число, равное произведению модулей векторов на косинус угла между ними: Векторы могут перемножаться скалярно. Скалярным произведением векторов a и b называется число, равное произведению модулей векторов на косинус угла между ними: ab = |a||b| cos Скалярное произведение коммутативно: ab = ba. Для перпендикулярных векторов ( = /2) равно нулю. При /2 ab 0 , при /2 (cos 0) ab 0.

Векторных произведений в физике очень много. В общем случае векторным произведением векторов a и b называется вектор c, модуль которого Векторных произведений в физике очень много. В общем случае векторным произведением векторов a и b называется вектор c, модуль которого |c| = |a||b| sin направление определяется по правилу правого буравчика: располагаем рукоятку штопора вдоль первого вектора a и вращаем ее по кратчайшему направлению ко второму вектору b , при этом поступательное движение острия штопора укажет направление вектора c . вектор c всегда перпендикулярен плоскости, в которой лежат перемножаемые векторы. На рисунке 9 приведен конкретный пример взаимного расположения всех трех векторов a , b и c.

В отличие от скалярного, векторное произведение не обладает свойством коммутативности, то есть результат векторного произведения зависит от порядка сомножителей. Например, если первым сомножителем будет b (c = [b a]), то на рисунке 9 вектор c будет направлен в противоположном направлении (т.е. вверх). Итак:
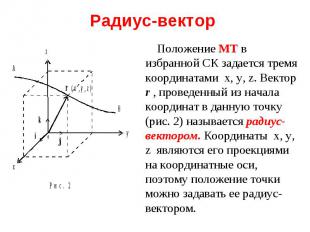

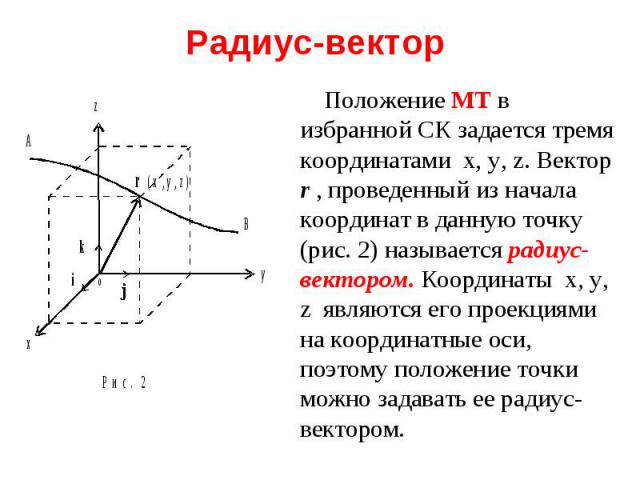
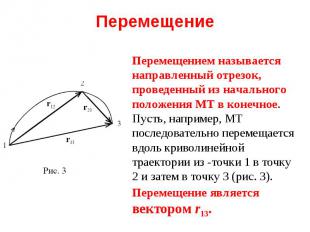
На рис. 2 три взаимно ортогональных единичных вектор i , j , k ( i = j = k = 1 ), называемые ортами, направлены вдоль соответствующих координатных осей. Радиус-вектор (как и любой другой вектор) можно записать в виде : На рис. 2 три взаимно ортогональных единичных вектор i , j , k ( i = j = k = 1 ), называемые ортами, направлены вдоль соответствующих координатных осей. Радиус-вектор (как и любой другой вектор) можно записать в виде : r = xi + yj + zk При этом компоненты вектора равны: rx= xi, ry= yj, rz= zi
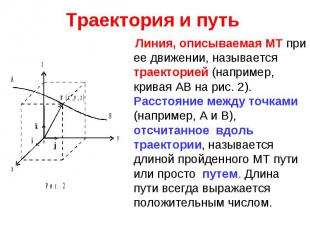
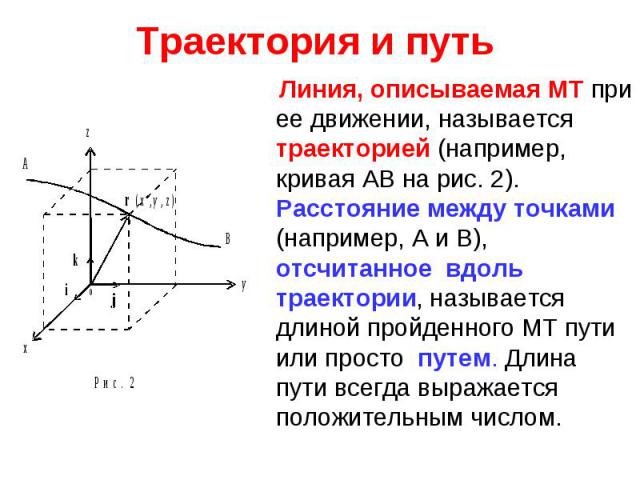
Линия, описываемая МТ при ее движении, называется траекторией (например, кривая АВ на рис. 2). Расстояние между точками (например, А и В), отсчитанное вдоль траектории, называется длиной пройденного МТ пути или просто путем. Длина пути всегда выражается положительным числом. Линия, описываемая МТ при ее движении, называется траекторией (например, кривая АВ на рис. 2). Расстояние между точками (например, А и В), отсчитанное вдоль траектории, называется длиной пройденного МТ пути или просто путем. Длина пути всегда выражается положительным числом.

Скорость – физическая величина, определяющая изменение координат тела со временем. Характеристика быстроты движения. Обозначим v, так как далее V будем обозначать объем. Зачем вообще вводить данную физическую величину? Скорость – физическая величина, определяющая изменение координат тела со временем. Характеристика быстроты движения. Обозначим v, так как далее V будем обозначать объем. Зачем вообще вводить данную физическую величину? Другие физические величины по разному зависят от скорости (например, линейно или квадратично). Verone Bugatti развивает скорость более 400 км/ч, а кинетическая энергия растет как квадрат скорости


Если за равные моменты времени МТ совершает одинаковые перемещения, то такое движение называется равномерным Если за равные моменты времени МТ совершает одинаковые перемещения, то такое движение называется равномерным v = const Если по прямой то – равномерное и прямолинейное (т.е. сохраняются и абсолютная величина скорости и направление движения или направление вектора ) Посмотрит опыт! Что для этого необходимо обсудим на следующей лекции.

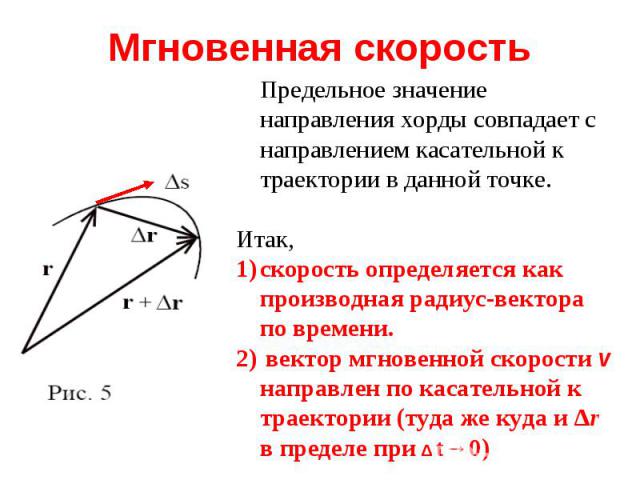
При достаточно малых t вектор перемещения r является хордой участка траектории (рис. 5). При дальнейшем уменьшении t в пределе получаем мгновенную скорость в данной точке траектории: Производная вектора сама является векторной величиной!
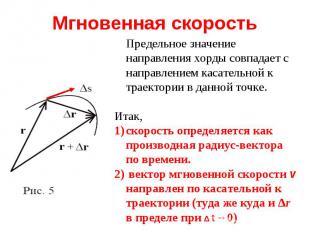

Дифференцируя по времени выражение с учетом постоянства единичных векторов (ортов) получаем выражение для скорости через ее компоненты: Дифференцируя по времени выражение с учетом постоянства единичных векторов (ортов) получаем выражение для скорости через ее компоненты: Проекциями производной вектора являются производные его проекций

Ускорение характеризует изменение скорости v с течением времени. Среднее ускорение за t равно: Ускорение характеризует изменение скорости v с течением времени. Среднее ускорение за t равно: Мгновенным ускорением, или ускорением в данной точке называется предельное значение aср при t→ 0 :

Дифференцируя по времени соотношение получаем: Дифференцируя по времени соотношение получаем: Ускорение характеризует изменение скорости как по величине, так и по направлению. В ряде случаев целесообразно разложить вектор a на две составляющие, одна из которых характеризует изменение скорости по величине, а другая – по направлению.
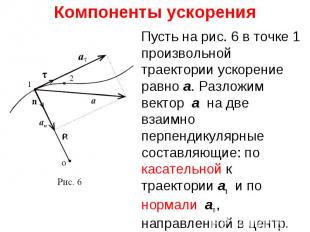
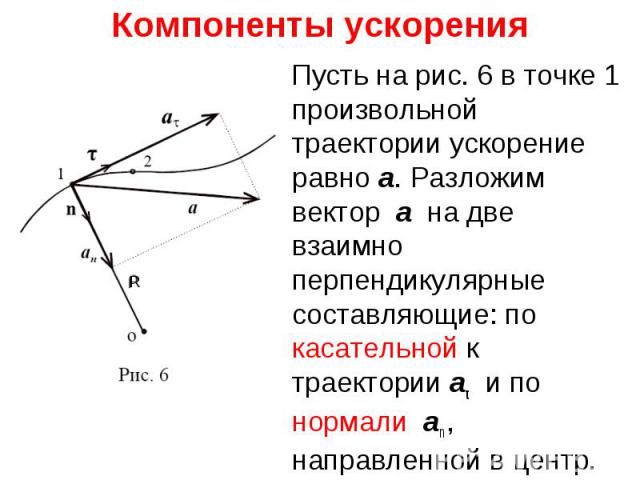
Пусть на рис. 6 в точке 1 произвольной траектории ускорение равно a. Разложим вектор a на две взаимно перпендикулярные составляющие: по касательной к траектории aτ и по нормали an , направленной в центр. Пусть на рис. 6 в точке 1 произвольной траектории ускорение равно a. Разложим вектор a на две взаимно перпендикулярные составляющие: по касательной к траектории aτ и по нормали an , направленной в центр.
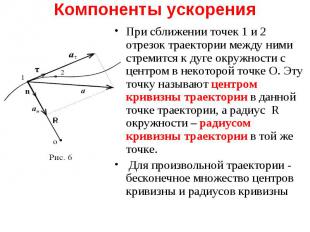
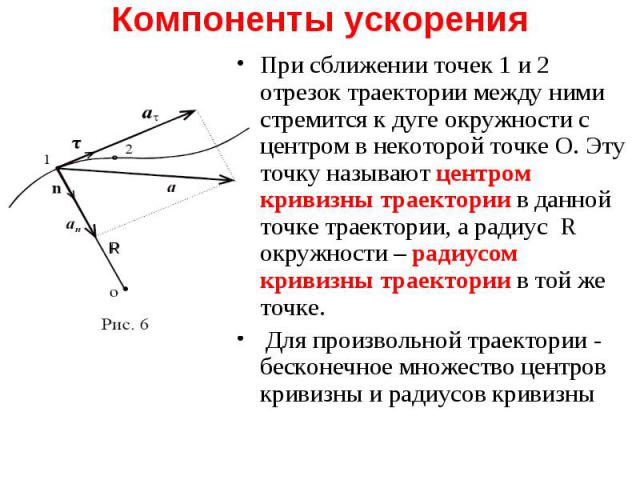
При сближении точек 1 и 2 отрезок траектории между ними стремится к дуге окружности с центром в некоторой точке О. Эту точку называют центром кривизны траектории в данной точке траектории, а радиус R окружности – радиусом кривизны траектории в той же точке. При сближении точек 1 и 2 отрезок траектории между ними стремится к дуге окружности с центром в некоторой точке О. Эту точку называют центром кривизны траектории в данной точке траектории, а радиус R окружности – радиусом кривизны траектории в той же точке. Для произвольной траектории - бесконечное множество центров кривизны и радиусов кривизны
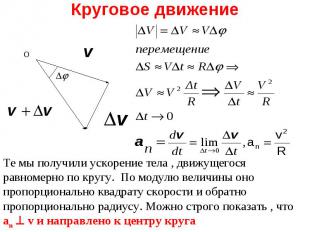

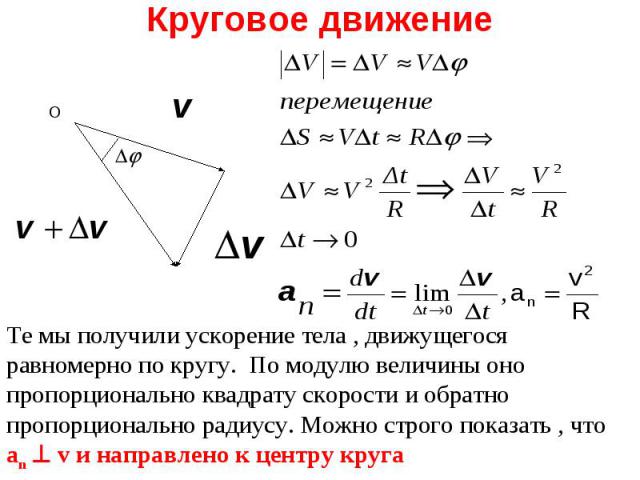
Т.е . Т.е . где n и - единичные векторы. an - называется нормальным (направлено по нормали к траектории), aτ - называется тангенциальным ускорением. В случае движения по окружности нормальное ускорение называется центростремительным, так как у окружности только один центр кривизны - центр окружности.


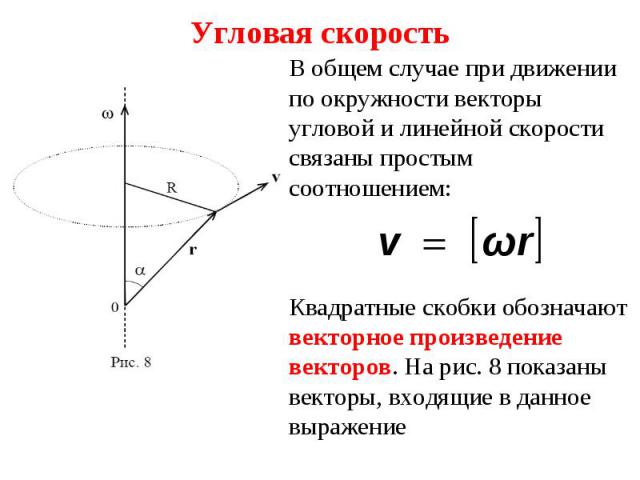
Пусть за малое время t радиус-вектор МТ повернулся на угол (рис. 7). Угловой скоростью точки называется вектор , модуль которого Пусть за малое время t радиус-вектор МТ повернулся на угол (рис. 7). Угловой скоростью точки называется вектор , модуль которого



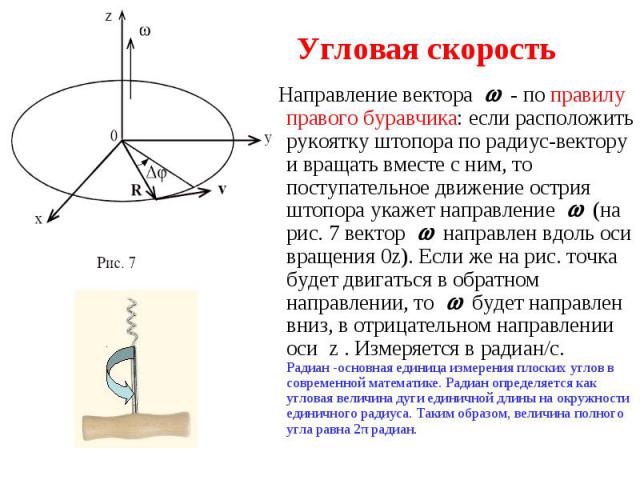
Направление вектора - по правилу правого буравчика: если расположить рукоятку штопора по радиус-вектору и вращать вместе с ним, то поступательное движение острия штопора укажет направление (на рис. 7 вектор направлен вдоль оси вращения 0z). Если же на рис. точка будет двигаться в обратном направлении, то будет направлен вниз, в отрицательном направлении оси z . Измеряется в радиан/с. Радиан -основная единица измерения плоских углов в современной математике. Радиан определяется как угловая величина дуги единичной длины на окружности единичного радиуса. Таким образом, величина полного угла равна 2π радиан. Направление вектора - по правилу правого буравчика: если расположить рукоятку штопора по радиус-вектору и вращать вместе с ним, то поступательное движение острия штопора укажет направление (на рис. 7 вектор направлен вдоль оси вращения 0z). Если же на рис. точка будет двигаться в обратном направлении, то будет направлен вниз, в отрицательном направлении оси z . Измеряется в радиан/с. Радиан -основная единица измерения плоских углов в современной математике. Радиан определяется как угловая величина дуги единичной длины на окружности единичного радиуса. Таким образом, величина полного угла равна 2π радиан.

Угловым ускорением называется производная угловой скорости по времени и напрямую связано с тангенциальным ускорением aτ : Угловым ускорением называется производная угловой скорости по времени и напрямую связано с тангенциальным ускорением aτ :











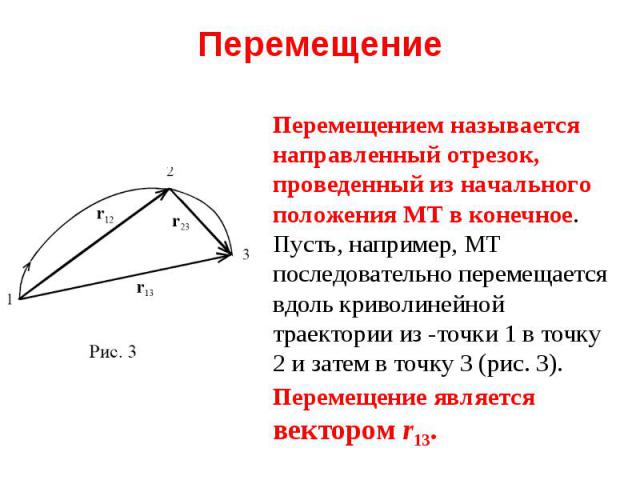
![В отличие от скалярного, векторное произведение не обладает свойством коммутативности, то есть результат векторного произведения зависит от порядка сомножителей. Например, если первым сомножителем будет b (c = [b a]), то на рисунке 9 вектор c будет … В отличие от скалярного, векторное произведение не обладает свойством коммутативности, то есть результат векторного произведения зависит от порядка сомножителей. Например, если первым сомножителем будет b (c = [b a]), то на рисунке 9 вектор c будет …](https://fs1.ppt4web.ru/images/95267/115020/640/img11.jpg)