Презентация на тему: Максимизация прибыли в краткосрочном периоде

Максимизация прибыли в краткосрочном периоде Выполнила Редок Полина, студентка ЭФ группы Э122Б

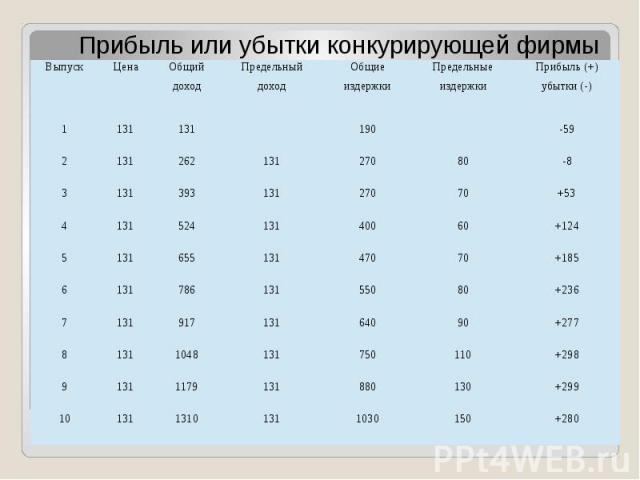
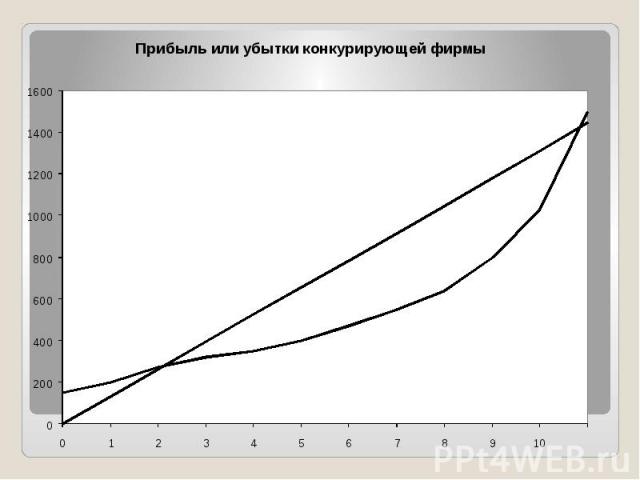
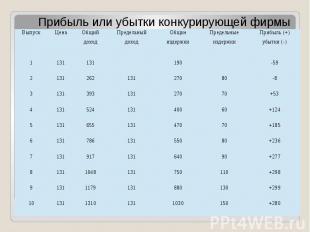
Принцип сопоставления валового дохода с валовыми издержками Перед производителем стоят три взаимосвязанных вопроса: Следует ли производить? 2. Если да, то какое количество продукции? 3. Какая прибыль (или убыток) будет получена?

Правильный ответ на 1 вопрос: Правильный ответ на 1 вопрос: Следует ли производить? — таков: фирме следует осуществлять производство в краткосрочном периоде, если она может получить либо 1) экономическую прибыль 2) убыток, который меньше, чем её постоянные издержки.

Ответ на 2 вопрос: в краткосрочном периоде фирме следует производить такой объем продукции, при котором она максимизирует прибыль или минимизирует убытки.

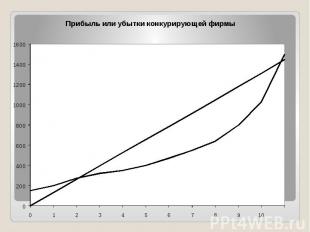
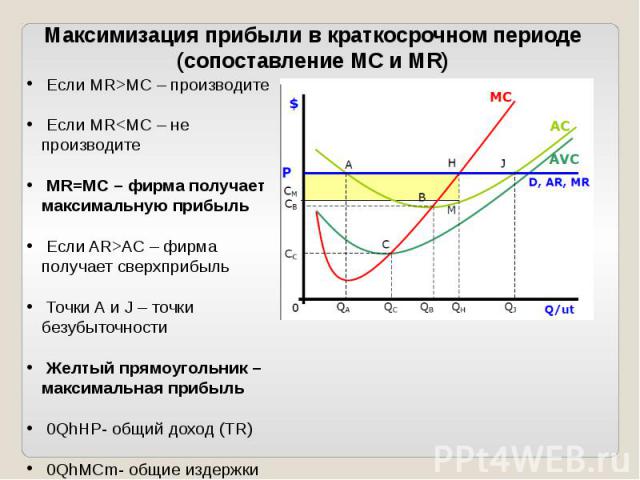
Принцип сопоставления предельного дохода с предельными издержками Альтернативным подходом к определению объемов продукции, которые конкурентная фирма захочет предложить на рынке по любой возможной цене, является определение и сравнение сумм, которые каждая дополнительная единица продукции будет добавлять к валовому доходу, с одной стороны, и к валовым издержкам — с другой

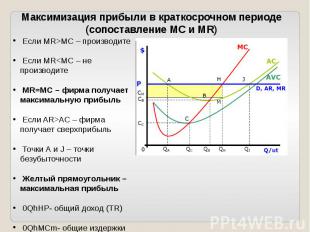
Отличительные черты этого правила

Задача!!! Рассмотрим конкурентную фирму, которая в краткосрочном периоде решает задачу максимизации прибыли. Рыночная цена продукции данной фирмы равна 16 рублям, а функция общих издержек фирмы имеет вид TC(Q)=Q(Q+4)+20, где ТС – издержки, измеряемые в рублях. Найди максимальную прибыль фирмы.

Правило максимизации прибыли MR = MC , для совершенно конкурентной фирмы P=MR, следовательно, Р=МС, МС(Q) = 2Q+4 = 16, откуда находим Q=6. Pr = 16Q-Q(Q+4)-20 = 16*6-6*10-20=16. Ответ: 16. Правило максимизации прибыли MR = MC , для совершенно конкурентной фирмы P=MR, следовательно, Р=МС, МС(Q) = 2Q+4 = 16, откуда находим Q=6. Pr = 16Q-Q(Q+4)-20 = 16*6-6*10-20=16. Ответ: 16. Можно также было решить другим способом. Выписать функцию прибыли. График данной функции это парабола, ветви направлены вниз, находим вершину параболы.

Спасибо за внимание!