Презентация на тему: Функциональные зависимости. Нормализация отношений

Функциональные зависимостиНормализация отношений

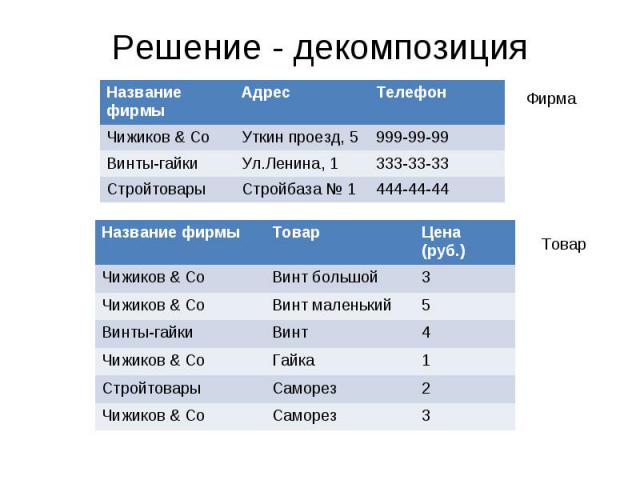
Пример плохого отношения

Недостатки ИзбыточностьАномалии измененияАномалии удаленияАномалии добавления

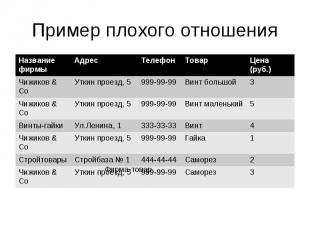
Решение - декомпозиция

Декомпозиция R {A1, A2, … An}S {B1, B2, … Bm}T {C1, C2, … Ck}1) {A1, A2, … An}= {B1, B2, … Bm} {C1, C2, … Ck}2) S= B1, B2, … Bm (R)3) T= C1, C2, … Ck (R)

Ограничения на значения: семантические, т.е. корректность отдельных значений (год рождения больше нуля);ограничения на значения, которые зависят только от равенства или неравенства значений (совпадают ли компоненты двух кортежей); наиболее важные ограничения называются функциональной зависимостью.

Функциональные зависимости R {A1, A2, … An}X, Y {A1, A2, … An}X Y если любому значению X соответствует в точности одно значение YX Y |Y(X=x(R))|1Название фирмы Адрес, телефон.Название фирмы, товар Цена

A1, A2, … An B1, B2, … Bm ФЗ бывают: Тривиальные {B1, B2, … Bm } {A1, A2, … An } Нетривиальные {B1, B2, … Bm } {A1, A2, … An } {A1, A2, … An } {B1, B2, … Bm } Полностью нетривиальные {A1, A2, … An } {B1, B2, … Bm } =

Ключ Ключ – набор атрибутов, который функционально определяет все остальныеF – множество функциональных зависимостей, заданных на отношении RAC называется транзитивной, если существует такой атрибут B, что имеются функциональные зависимости AB и BC и отсутствует функциональная зависимость CA

Замыкание множества атрибутов R {A1, A2, … An}{B1, B2, … Bm } {A1, A2, … An }F – мн-во ФЗZ={B1, B2, … Bm }+ Z0 := {B1, B2, … Bm }BiBj CZ1:=Z0C{B1, B2, … Bm } += {A1, A2, … An } {B1, B2, … Bm } - ключ

Пример R {A, B, C, D, E, F} S = {AD, ABE, BFE, CDF, EC} {AE}+ ?

Пример R {A, B, C, D, E, F} S = {AD, ABE, BFE, CDF, EC} {AE}+ = ACDEF

Аксиомы Армстронга если BA, то AB рефлексивность;если AB, то ACBC пополнение;если AB и BC, то AC транзитивность.

Правила вывода(из аксиом Армстронга) 1. ОбъединениеЕсли XY и XZ, то XYZ.XY + А2 = XXY, XZ + A2 = YXYZ + A3 = XYZ2. Псевдотранзитивность XY и WYZ, то WXZ.XY +A2 = WXWY. WYZ + A3 = WXZ.3. ДекомпозицияЕсли XY и ZY, то XZ.А1 + А3.

Замыкание множества функциональных зависимостей F+ - множество всех зависимостей, которые можно вывести из F, называют замыканием множества ФЗ F Любое множество функциональных зависимостей, из которого можно вывести все остальные ФЗ, называется базисомЕсли ни одно из подмножеств базиса базисом не является, то такой базис минимален

Замыкание множества функциональных зависимостей R {A1, A2, … An}F – мн-во ФЗB1, B2, … Bm C (B1, B2, … Bm C) F+ , ifC{B1, B2, … Bm }+

Пример: R (A, B, C, D)AB C, C D, DAНайти все нетривиальные ФЗ, которые следуют из заданныхВозможные ключи

Покрытие множества функциональных зависимостей Множество ФЗ F2 называется покрытием множества ФЗ F1, если любая ФЗ, выводимая из F1, выводится также из F2.F1+F2+F1 и F2 называются эквивалентными, если F1+ = F2+.

Минимальное покрытие множества функциональных зависимостей правая часть любой ФЗ из F является множеством из одного атрибута (простым атрибутом);удаление любого атрибута из левой части любой ФЗ приводит к изменению замыкания F+;удаление любой ФЗ из F приводит к изменению F+.

Декомпозиция Декомпозиция – это разбиение на множества, может быть пересекающиеся, такие, что их объединение – это исходное отношение.Восстановить исходное отношение можно только естественным соединением.Говорят, что декомпозиция обладает свойством соединения без потерь, если для любого отношенияr = R1(r) R2(r) ... Rn(r).

А что происходит с зависимостями при декомпозиции? Можно определить Z(F): XY XYZДекомпозиция сохраняет множество зависимостей, если из объединения всех проекций зависимостей логически следует F.

Проектирование реляционных отношений 1 нормальная форма (НФ)– значения не являются множествами и кортежами.Атрибут называется первичным, если входит в состав любого возможного ключа.2 нормальная форма – 1 НФ + любой атрибут, не являющийся первичным, полностью зависит от любого его ключа, но не от подмножества ключа.Фирма, Адрес, Телефон, Товар, Цена

3 НФ Транзитивная зависимость: пусть A, B, C – атрибуты, AB, BC, A не зависит от B и B не зависит от C. Тогда говорят, что C транзитивно зависит от A.3 нормальная форма – если отношение находится во 2 нормальной форме и любой атрибут, не являющийся первичным, нетранзитивно зависит от любого возможного ключа.

Примеры: Универмаг, Товар, Номер отдела, ЗаведующийГород, Индекс, Адрес

Примеры: 3 нормальная форма – (Город, Индекс, Адрес)2 нормальная форма, но не 3 нормальная форма – (Универмаг, Товар, Номер отдела, Заведующий)УТН, УНЗ, ключ – УТ.

НФ Бойса-Кодда Нормальная форма Бойса–Кодда – если XA, AX, то Xключ R.(Город, Индекс, Адрес) – 3 нормальная форма, но не форма Бойса–Кодда. Если разобьем на две (Город, Индекс), (Индекс, Адрес), пропадает зависимость Город, АдресИндекс.

НФ Бойса-Кодда (Город, Индекс, Адрес) – 3 нормальная форма, но не форма Бойса–Кодда. Если разобьем на две (Город, Индекс), (Индекс, Адрес), пропадает зависимость Город, АдресИндекс.

Вывод: Каждая схема отношений может быть приведена к форме Бойса–Кодда, так что декомпозиция обладает свойством соединения без потерь.Любая схема может быть приведена к 3 нормальной форме с соединением без потерь и с сохранением функциональной зависимости.Но не всегда можно привести к форме Бойса–Кодда с сохранением функциональных зависимостей.

Шаги при декомпозиции Находим минимальное покрытие множества функциональных зависимостейВыделяем зависимость, нарушающую НФX Y (и нет атрибутов, зависящих от Y).Находим зависимости с такой же левой частью. X W, X ZВыделяем в отдельное отношение XYWZИз исходного отношения удаляем YWZ

Пример S Студент G ГруппаH ВремяR АудиторияC ПредметT Преподаватель