Презентация на тему: Деревья (trees)

Деревья (trees) «…великое Дерево Жизни заполняет земную кору своими мертвыми и сломанными ветвями и покрывает поверхность вечно ветвящимися и прекрасными побегами»Ч. Дарвин

Задача построения филогенетического дерева The time will come, I believe, though I shall not live tosee it, when we shall have fairly true genealogical treesof each great kingdom of Nature. Биологические задачи – сравнение 3-х и более объектов (кто на кого более похож .... ) реконструкция эволюции (кто от кого, как и когда произошел…) Математическая задача – задача кластеризации, использование теории графов и комбинаторной оптимизации для того, чтобы на основе «грязных» биологических данных получить разумное с точки зрения эксперта-биолога дерево.

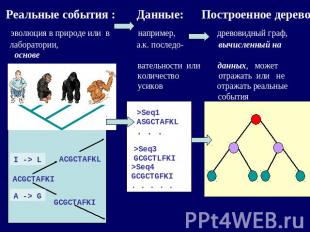
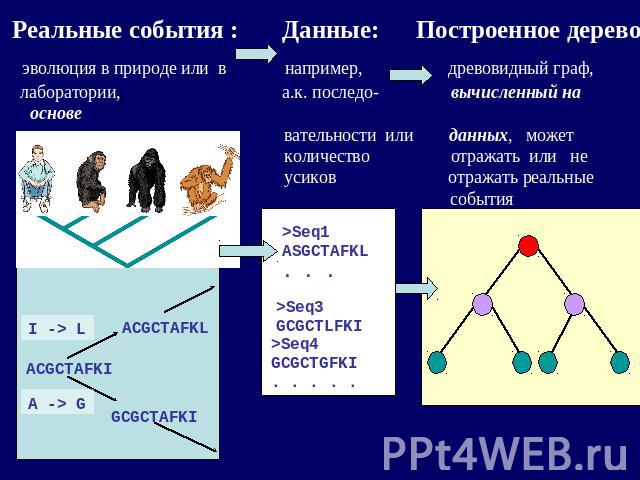
Реальные события : Данные: Построенное дерево эволюция в природе или в например, древовидный граф, лаборатории, а.к. последо- вычисленный на основе компьютерная симуляция вательности или данных, может количество отражать или не усиков отражать реальные события

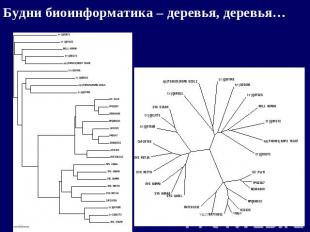
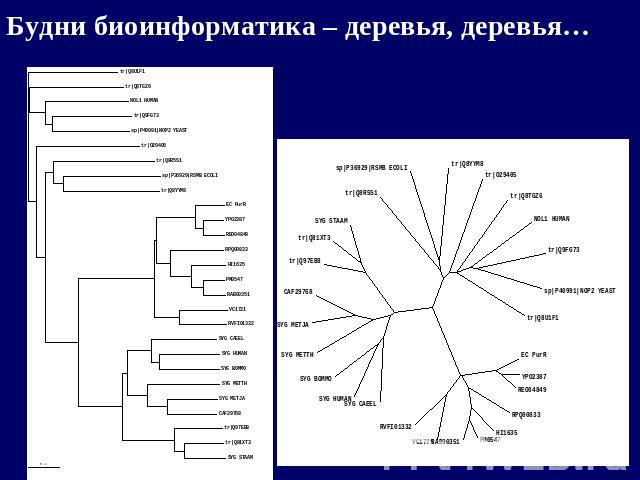
Будни биоинформатика – деревья, деревья…

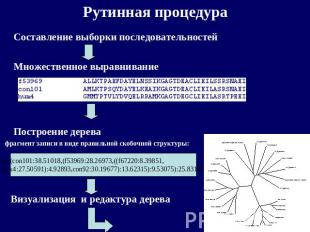
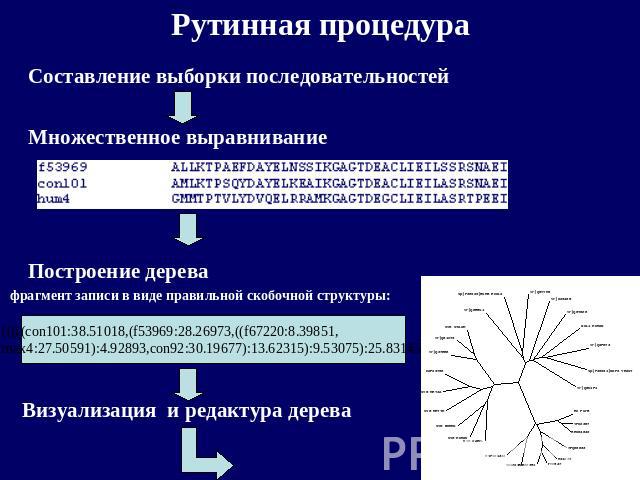
Рутинная процедура Составление выборки последовательностей Множественное выравнивание Построение дерева фрагмент записи в виде правильной скобочной структуры: Визуализация и редактура дерева

Основные термины

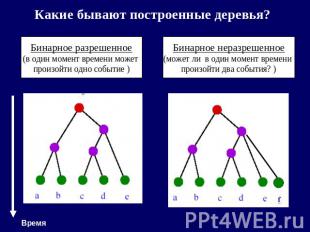
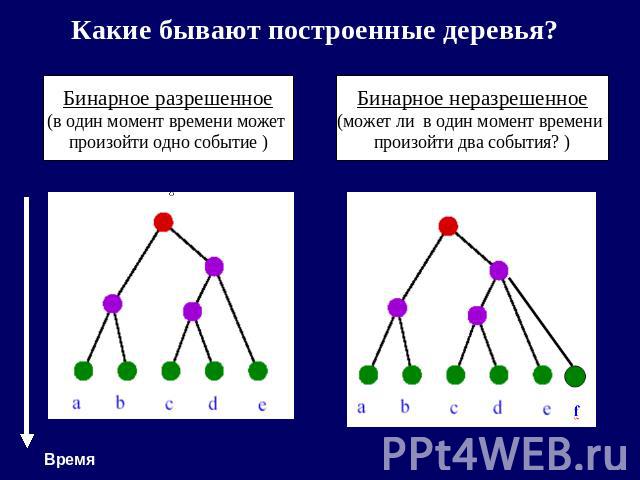
Какие бывают построенные деревья? Бинарное разрешенное(в один момент времени может произойти одно событие ) Бинарное неразрешенное (может ли в один момент времени произойти два события? )

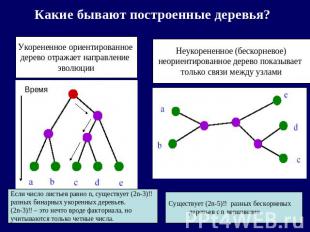
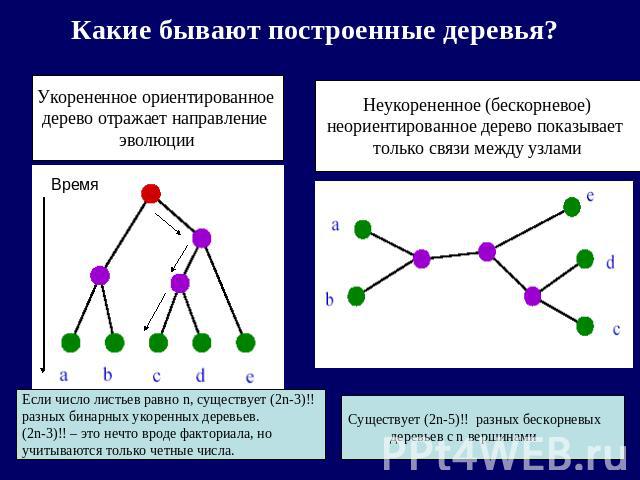
Какие бывают построенные деревья? Укорененное ориентированное дерево отражает направление эволюции Неукорененное (бескорневое)неориентированное дерево показывает только связи между узлами Если число листьев равно n, существует (2n-3)!!разных бинарных укоренных деревьев.(2n-3)!! – это нечто вроде факториала, но учитываются только четные числа. Существует (2n-5)!! разных бескорневых деревьев с n вершинами

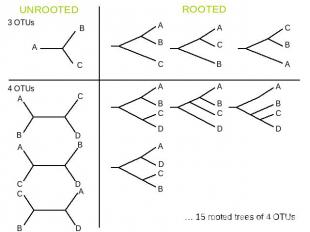
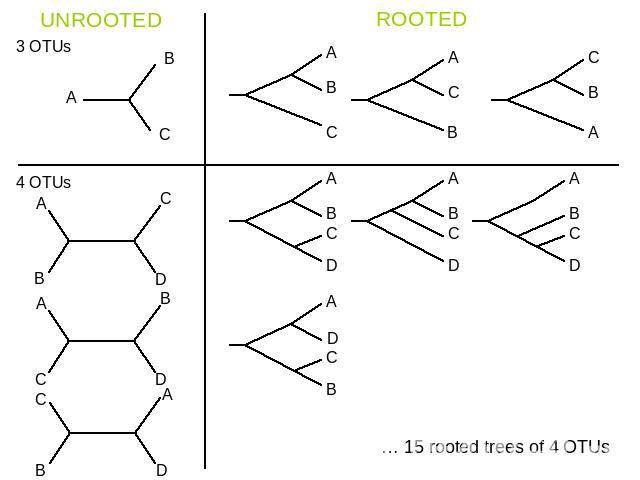
UNROOTED ROOTED … 15 rooted trees of 4 OTUs

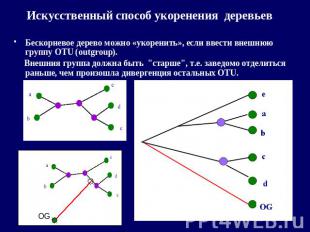
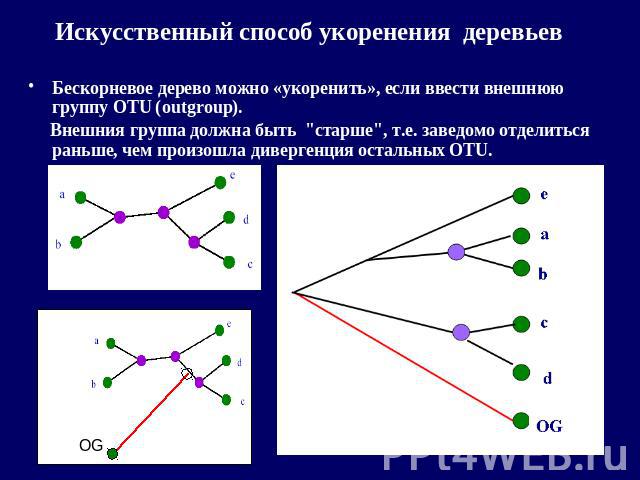
Искусственный способ укоренения деревьев Бескорневое дерево можно «укоренить», если ввести внешнюю группу OTU (outgroup). Внешния группа должна быть "старше", т.е. заведомо отделиться раньше, чем произошла дивергенция остальных OTU.

Какие бывают построенные деревья ? Расстояние по дереву не то же самое, что эволюционное расстояние между данными Ультраметрические деревья Корневое дерево, в котором для любых листьев i и j расстояние D(i,j) – метка наименьшего общего предка i и j . В таком дереве все листья находятся на одинаковом от корня, что соответствует одинаковой скорости эволюции всех ветвейАддитивные деревья Дерево, в котором для любых вершин i и j расстояние D(i,j) – это эволюционный путь от i к j . При этом расстояния от i и от j до их наименьшего общего предка могут сильно различаться. Другие … Вообще говоря, строгое решение задачи построения аддитивного дерева невозможно (следует из свойства задачи)

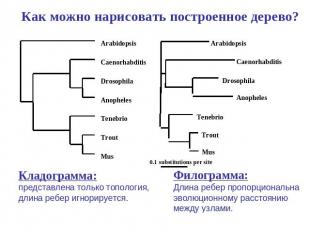
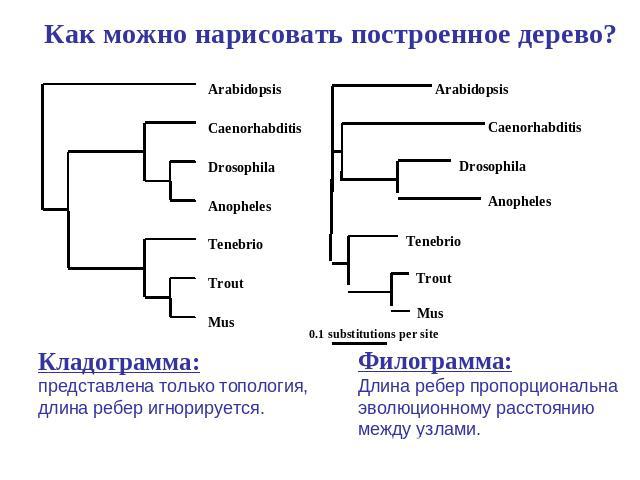
Как можно нарисовать построенное дерево? Кладограмма: представлена только топология, длина ребер игнорируется. Филограмма:Длина ребер пропорциональна эволюционному расстоянию между узлами.

Основные алгоритмы построения филогенетических деревьев Методы, основанные на оценке расстояний (матричные методы):Вычисляются эволюционные расстояния между всеми вершинами(OTUs) и строится дерево, в которомрасстояния между вершинаминаилучшим образом соответствуютматрице попарных расстояний.UPGMA (Unweighted Pair Group with Arithmetic Mean)Ближайших соседей (Neighbor-joining, NJ) Символьно-ориентированные методы:Наибольшего правдоподобия, Maximum likelihood, ML Используется модель эволюции и строится дерево, которое наиболее правдоподобно при данной моделиМаксимальной экономии (бережливости), maximum parsimony, MP Выбирается дерево с минимальным количеством мутаций, необходимых для объяснения данных

Методы, основанные на оценке расстояний Дано: М – матрица n x n, где Mij>=0 , Mij – эволюционное расстояние между листьями (OTU).Задача: Построить реберно взвешенное (an edge-weighted) дерево, где каждая вершина (лист) соответствует объекту из M , а расстояние, измеренное по дереву между вершинами (листьями) i and j соответствует Mij.

UPGMA (алгоритм последовательной кластеризации) Выбираем 2 наиболее похожие вершины a, c.Строим новый узел k такой, что D(a,k)=D(b,k)=D(a,c)/2.Пересчитываем матрицу попарных расстояний : D(b, a or c) = [ D(b,a) + D(b,c) ] /2 = (8+9)/2=8.5D(d, a or c) = [ D(d,a) + D(d,c) ] /2=(12+11)/2=11.5Повторяем процедуру…. В конце концов получаем единственное ультраметрическое укорененное дерево=11.5

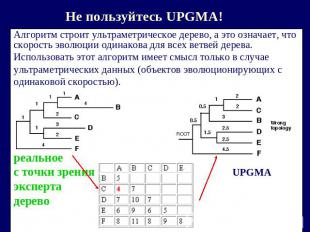
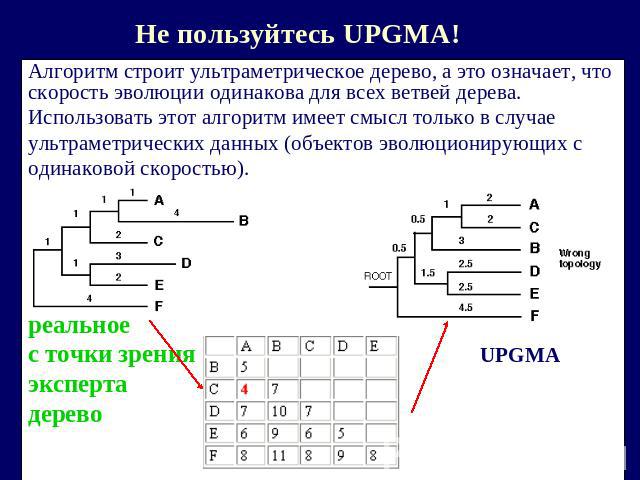
Не пользуйтесь UPGMA! Алгоритм строит ультраметрическое дерево, а это означает, что скорость эволюции одинакова для всех ветвей дерева.Использовать этот алгоритм имеет смысл только в случае ультраметрических данных (объектов эволюционирующих содинаковой скоростью).реальное c точки зрения UPGMAэкспертадерево

Метод ближайших соседей (Neighbor-joining, NJ) 1. Рисуем «звездное» дерево и будем "отщипывать" от него по паре вершин, рассмотрим все возможные пары вершины. пусть - «среднее» расстояние до других вершин.2. Выберем 2 вершины i и j с минимальным значением Mij – ui –uj т.е. выбираем 2 узла, которые близки друг к другу, но далеки ото всех остальных.

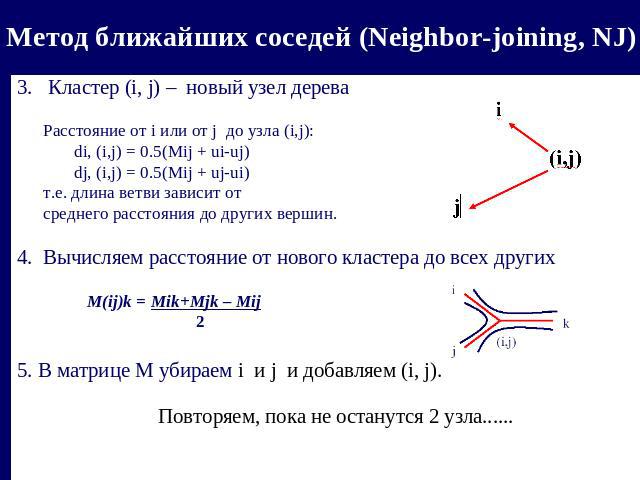
Метод ближайших соседей (Neighbor-joining, NJ) 3. Кластер (i, j) – новый узел дерева Расстояние от i или от j до узла (i,j): di, (i,j) = 0.5(Mij + ui-uj) dj, (i,j) = 0.5(Mij + uj-ui) т.е. длина ветви зависит от среднего расстояния до других вершин.4. Вычисляем расстояние от нового кластера до всех других M(ij)k = Mik+Mjk – Mij 25. В матрице М убираем i и j и добавляем (i, j). Повторяем, пока не останутся 2 узла......

Метод ближайших соседей (Neighbor-joining, NJ) Строит бескорневое аддитивное деревоМожет работать с большим количеством данныхДостаточно быстрый алгоритмХорошо зарекомендовал себя на практике: если есть недвусмысленное с точки зрения эксперта дерево, то оно будет построено.Используется при множественном выравнивании с помощью программы ClustalWМогут появиться ветви с длиной <0

Достоверность топологии. Bootstraps. Есть множественное выравнивание и построенное по нему дерево. Верим ли мы в топологию дерева? Создадим псевдоданные: N множественных выравниваний той же длины, что и исходное, каждое из псевдовыравниваний - случайный набор столбцов из исходного.Построим N деревьев: на каждом внутреннем узле отметим долю случаев из N, в которых появлялся этот узел. Обычно верят в топологию, если метки узлов на бутстрепном дереве больше 70-80% . Если меньше 30%, то не верим. В иных случаях – думаем…

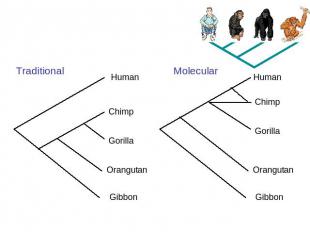
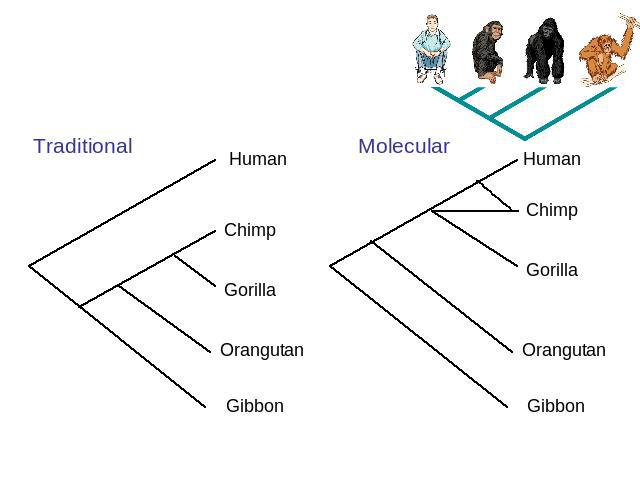
Traditional Molecular

Trees plagiarized by Chuck Staben, 1998Sergeant Joyce Kilmer, 1914