Презентация на тему: Задания на проценты

Работа: 1)Учителя математики Зениной Алевтины Дмитриевны 2)Учителя математики Савченко Е.М. МОУ гимназия №1, г.Полярные Зори 900igr.net

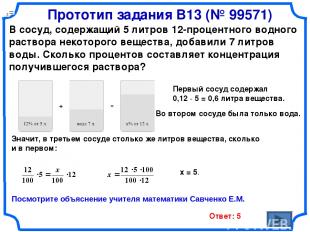
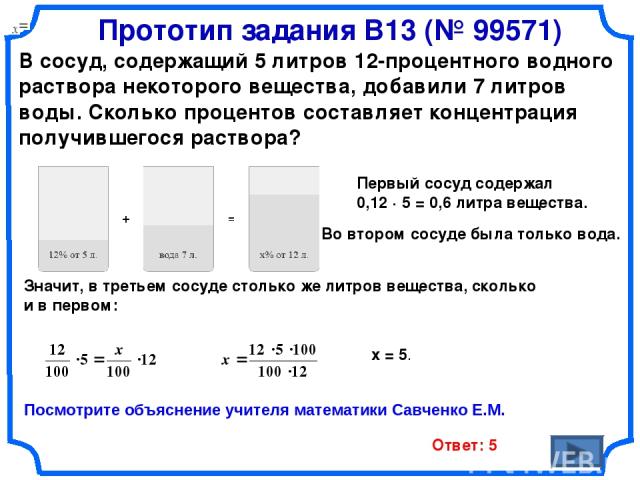
Прототип задания B13 (№ 99571) В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора? Значит, в третьем сосуде столько же литров вещества, сколько и в первом: х = 5. Ответ: 5 Первый сосуд содержал 0,12 · 5 = 0,6 литра вещества. Во втором сосуде была только вода. Посмотрите объяснение учителя математики Савченко Е.М.

В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора? 12% = 0,12 Прототип задания B13 (№ 99571)

Прототип задания B13 (№ 99572) Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора? В результате получили раствор массой 2х. Получаем: 0,15х + 0,19х = 0,34х Ответ: 17. Или 0,34х 2х = 0,17 = 17% Пусть масса первого раствора равна х. Масса второго — тоже х . 0,34x представим как 0,17 · 2х Переведем в проценты 0,17 = 17% 0,34х = 0,17·2х Посмотрите объяснение учителя математики Савченко Е.М.

Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора? x x Весь р-р Вещества в растворе 0,15x 0,19x x x 0,15x 0,19x + Упростим: Прототип задания B13 (№ 99572)

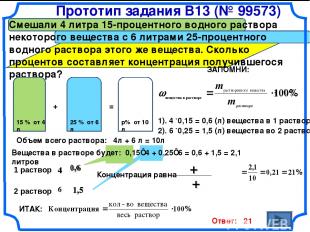
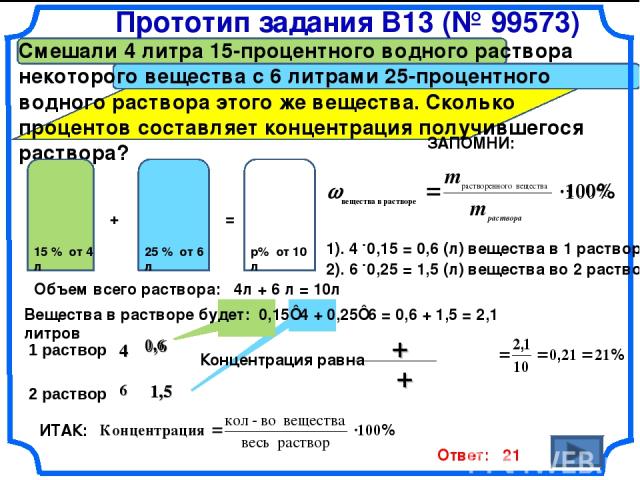
Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? Прототип задания B13 (№ 99573) 15 % от 4 л + 25 % от 6 л = Объем всего раствора: 4л + 6 л = 10л р% от 10 л Ответ: 21 6 4 4 6 0,6 1,5 0,6 1,5 + Вещества в растворе будет: 0,15⋅4 + 0,25⋅6 = 0,6 + 1,5 = 2,1 литров Концентрация равна ИТАК: ЗАПОМНИ:

Прототип задания B13 (№ 99574) Виноград содержит 90% влаги, а изюм  — 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма? Внимание! Если вам встретилась задача «о продуктах», то есть такая, где из винограда получается изюм, из абрикосов урюк, из хлеба сухари или из молока творог — знайте, что на самом деле это задача на растворы. Виноград мы тоже можем условно изобразить как раствор. В нем есть вода и «сухое вещество». У «сухого вещества» сложный химический состав, а по его вкусу, цвету и запаху мы могли бы понять, что это именно виноград, а не картошка. Изюм получается, когда из винограда испаряется вода. При этом количество «сухого вещества» остается постоянным. В винограде содержалось 90% воды, значит, «сухого вещества» было 10%. В изюме 5% воды и 95% «сухого вещества». . х = 190 Ответ: 190. Пусть из х кг винограда получилось 20 кг изюма. Тогда 10% от х = 95% от 20 Составим уравнение: 0,1х = 0,95 · 20 ИЛИ

Прототип задания B13 (№ 99574) Виноград содержит 90% влаги, а изюм  — 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма? Проследим за количеством сухого вещества в винограде и изюме. 190(кг) винограда надо взять. Ответ: 190 Второй способ объяснения: 0,1х х Пусть х (кг), винограда требуется для получения 20 кг изюма. 20 В винограде 90% влаги, значит 10% сухого вещества. В изюме 5% влаги, значит 95% сухого вещества от 20кг изюма. 0,95∙20 Уравняем количество сухого вещества в винограде и изюме, составив уравнение 0,1х = 0,95·20; 0,1х = 19; х = 190 Посмотрите объяснение учителя математики Савченко Е.М. Сухое вещество Количество в кг Виноград Изюм

это 19 кг 90% 95% 10% Виноград содержит 90% влаги, а изюм  — 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма? Сухое вещество Влага 5% 20 кг изюма это 19 кг 19 кг сухого вещества в винограде – это 10% всего винограда 2). 19 : 0,1 = 190 (кг) сухого винограда надо взять. Прототип задания B13 (№ 99574)

Прототип задания B13 (№ 99575) Имеется два сплава. Первый содержит 10% никеля, второй  — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго? Пусть масса первого сплава равна х , а масса второго равна у. Запишем простую систему уравнений: Ответ: 100 В результате получили сплав массой х + у = 200. Масса никеля: (10% от х) + (30% от у) = (25% от 200) Посмотрите объяснение учителя математики Савченко Е.М.

0,3y 0,1x y x y x Имеется два сплава. Первый сплав содержит 10% никеля, второй  — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго? Весь сплав, кг Никеля, кг 0,1x 0,3y = 25 Составь и реши систему уравнений Прототип задания B13 (№ 99575)

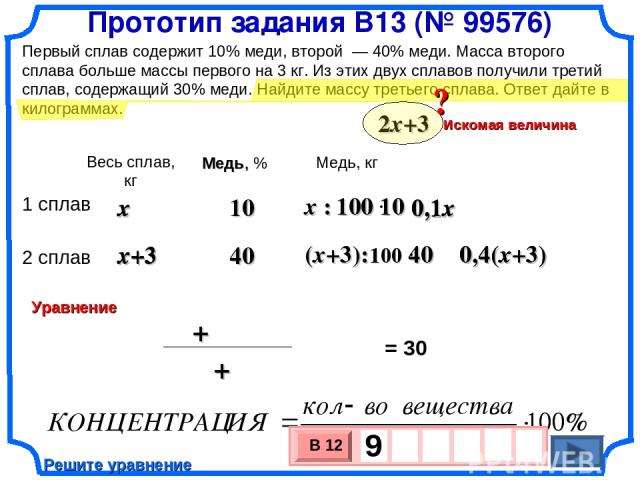
Прототип задания B13 (№ 99576) Первый сплав содержит 10% меди, второй  — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. 3-ой сплав x+3 40% от (х+3) 0,4(х+3) 0,3(2x+3) 0,1х + 0,4(х+3) = 0,3(2x+3) 0,1х + 0,4х + 1.2 = 0,6x + 0,9 0,1х =0,3 х = 3 2х +3 = 9 ОТВЕТ: 9

Прототип задания B13 (№ 99576) Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3 килограмма. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в кг. Меди в третьем сплаве 30%, значит масса меди в третьем сплаве 0,3 (2х +3). 0,1х + 0,4х + 1,2 =0,6х + 0,9 3(кг) масса первого сплава, масса третьего сплава 9 кг. Ответ: 9 кг. Проследим за количеством меди в каждом сплаве. Пусть х(кг) масса первого сплава, (х + 3)кг масса второго сплава. х х+3 Меди в первом сплаве 10%, значит масса меди в первом сплаве 0,1х. 0,1х Меди во втором сплаве 40%, значит масса меди во втором сплаве 0,4(х + 3). 0,4 (х + 3) Масса третьего сплава (х + х + 3). х + х + 3 0,3 (2х + 3) Составим уравнение, исходя из количества меди в каждом сплаве 0,1х + 0,4 (х + 3) = 0,3 ( 2х + 3) х = 3 -0,1х = -0,3; Посмотрите объяснение учителя математики Савченко Е.М. Медь Масса сплава в кг I сплав II сплав III сплав

0,4(x+3) 0,4(x+3) x+3 0,1x x+3 x x Первый сплав содержит 10% меди, второй  — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. Весь сплав, кг Медь, кг 0,1x = 30 Решите уравнение Прототип задания B13 (№ 99576)

Прототип задания B13 (№ 99577) Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси? Получили (х+у+10) кг раствора, в котором (0,3х+0,6у) кислоты. ОТВЕТ: 60 х - масса 30%-ого раствора кислоты, в котором 0,3х «чистой» кислоты у - масса 60%-ого раствора кислоты, в котором 0,6у «чистой» кислоты Дальше считают концентрацию, деля часть на целое.

Прототип задания B13 (№ 99577) Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси? Решение: _ : 5 · :30 _ ОТВЕТ: 60 Посмотрите объяснение учителя математики Савченко Е.М.

0,6y 0,6y 0,3x y Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси? x y Весь р-р Вещества в растворе 0,3x x + 1 уравнение + 10 = 36 Составь и реши систему уравнений Прототип задания B13 (№ 99577)

0,6y 0,6y 0,3x y Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси? Прототип № 99577 Составим второе уравнение. x y Весь р-р Вещества в растворе 0,3x x + 2 уравнение + 10 = 41 + 5 ? Искомая величина Составь и реши систему уравнений

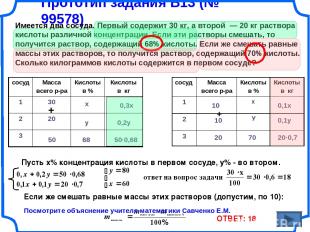
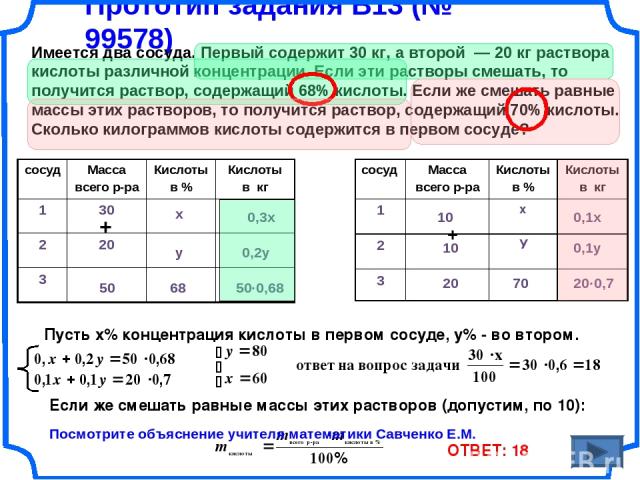
Прототип задания B13 (№ 99578) Имеется два сосуда. Первый содержит 30 кг, а второй  — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде? Если же смешать равные массы этих растворов (допустим, по 10): + 50 Пусть х% концентрация кислоты в первом сосуде, у% - во втором. х у 68 0,3х 0,2у 50·0,68 10 10 + 20 70 0,1х 0,1у 20·0,7 ОТВЕТ: 18 Посмотрите объяснение учителя математики Савченко Е.М. сосуд Масса всего р-ра Кислоты в % Кислоты в кг 1 30 2 20 3 сосуд Масса всего р-ра Кислоты в % Кислоты в кг 1 х 2 У 3

20 30 Имеются два сосуда. Первый содержит 30 кг, а второй  — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде? Весь р-р, кг Кислоты, кг 0,3x 0,2y = 68 30 20 0,3x 0,2y Составь и реши систему уравнений Искомая величина Прототип задания B13 (№ 99578)

0,01y 0,01x 1 1 1 1 Имеются два сосуда. Первый содержит 30 кг, а второй  — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде? Весь р-р, кг Кислоты, кг 0,01x 0,01y = 70 Возьмем по 1 кг Составь и реши систему уравнений Прототип задания B13 (№ 99578)