Презентация на тему: Задачи на логику

Решение логических задач 900igr.net

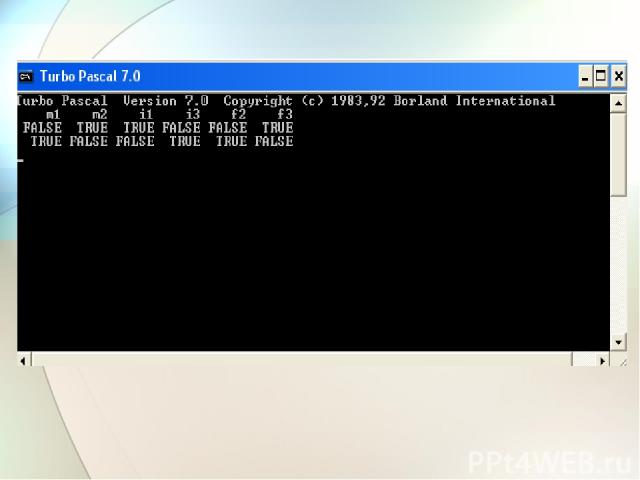
Введение В презентации рассмотрены основные способы формализации условий задач и их решения: алгебраический, табличный, графический, метод диаграмм Эйлера-Венна. При решении задачи №1 и №2 применен алгебраический метод. Наиболее трудным является перевод условия задачи на язык формальной логики, при этом необходимо знать законы логики и уметь преобразовывать логические выражения. Но этот метод позволяет реализовать решение задачи на любом языке программирования. В качестве примера представлен программный код на языке Turbo Pascal и результат выполнения программы задачи №1.

Решение задачи №3 предложено в виде таблицы. Этот метод нагляден, но требует анализа информации, представленной в таблице, умения сравнивать и сопоставлять данные. Метод графов применяет тогда, когда между объектами существует много связей. Графы позволяет наглядно представить эти связи и определить, какие из них не противоречат условии задачи (задача №4). Задача №5 решена с помощью диаграмм Эйлера-Венна на основе теории множеств.

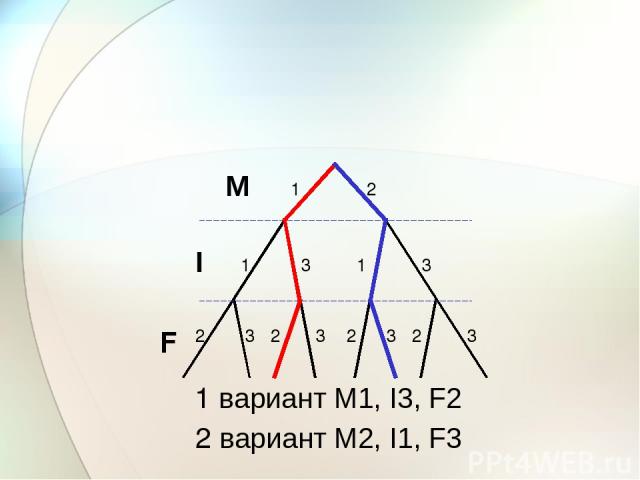
Задача 1 Учитель математики просит поставить ему первый или второй урок, учитель информатики – первый или третий, а учитель физики – второй или третий уроки. Какие варианты расписания можно составить, учитывая пожелания учителей?

Логические переменные: М1 - математика 1 урок М2 - математика 2 урок I1 - информатика 1 урок I3 - информатика 3 урок F2 - физика 2 урок F3 - физика 3 урок

1) M1 or M2 = 1 I1 or I3 = 1 F2 or F3 = 1 2) M1 and M2 = 0 I1 and I3 = 0 F2 and F3 = 0 M1 and I1 = 0 M2 and F2 = 0 I3 and F3 = 0

M1 and M2 = 0 Not(M1 and M2 = 0) = not M1 or not M2 = 1

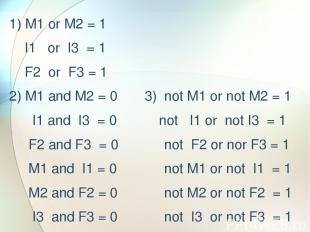
1) M1 or M2 = 1 I1 or I3 = 1 F2 or F3 = 1 2) M1 and M2 = 0 3) not M1 or not M2 = 1 I1 and I3 = 0 not I1 or not I3 = 1 F2 and F3 = 0 not F2 or nor F3 = 1 M1 and I1 = 0 not M1 or not I1 = 1 M2 and F2 = 0 not M2 or not F2 = 1 I3 and F3 = 0 not I3 or not F3 = 1

(m1 or m2) and (i1 or i3) and (f2 or f3) and (not m1 or not m2) and (not i1 or not i3) and (not f2 or not f3) and (not m1 or not i1) and (not m2 or not f2) and (not i3 or not f3) = 1

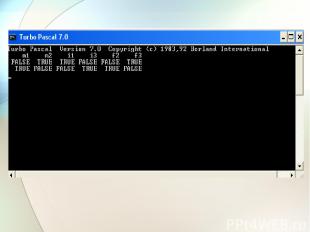
var m1,m2,i1,i3,f2,f3,a: boolean; begin writeln ('m1':6,'m2':6,'i1':6,'i3':6,'f2':6,'f3':6); for m1:=false to true do for m2:=false to true do for i1:=false to true do for i3:=false to true do for f2:=false to true do for f3:=false to true do begin a:=(m1 or m2) and (i1 or i3) and (f2 or f3) and (not m1 or not m2) and (not i1 or not i3) and (not f2 or not f3) and (not m1 or not i1) and (not m2 or not f2) and (not i3 or not f3); if a= true then writeln (m1:6,m2:6,i1:6,i3:6,f2:6,f3:6) end; readln; end.

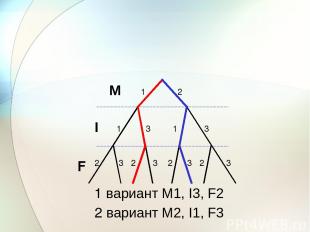
М I F 1 2 3 1 1 3 3 2 3 3 3 2 2 2 1 вариант M1, I3, F2 2 вариант M2, I1, F3

Задача 2 Алеша, Боря и Гриша нашли в земле сосуд. Рассматривая в земле удивительную находку, каждый высказал по два предположения: Алеша. Это сосуд греческий и изготовлен в V веке. Боря. Это сосуд финикийский и изготовлен в III веке. Гриша. Это сосуд не греческий и изготовлен в IV веке.

Учитель истории сказал ребятам, что каждый из них прав в только в одном из двух предположений. Где и в каком веке изготовлен сосуд?

G = сосуд греческий F = сосуд финикийский V3 = изготовлен в III в. V4 = изготовлен в IV в. V5 = изготовлен в V в.

А. G and (not V5) or (not G) and V5 =1 Б. F and (not V3) or (not F) and V3 =1 Г. (not G) and (not V4) or G and V4 =1 V3*(not V4)*(not V5) + (not V3)*V4*(not V5) + + (not V3)*(not V4)*V5=1 F*(not G) + (not F)*G = 1 Имеем 5 тождественно истинных высказываний. Перемножим их.

(G *(not V5)+(not G) * V5)* (F *(not V3)+(not F) * V3)* ((not G) *(not V4)+G * V4)* (V3 *(notV4)*(notV5)+(notV3) * V4 * (notV5) + (notV3) * (notV4) * V5)* (F*(not G) + (not F)*G) = 1 перемножим 1 и 3 скобки, затем 2 и 5, упростим выражения, учитывая G*(not G)=0 G*G=G, (not G)*(not G)=(not G)

(G*(notV5)*V4 + (notG)*V5*(notV4))* (F*(notV3)*(notG) + (notF)*V3*G)* (V3*(notV4)*(notV5)+(notV3)*V4*(notV5)+(notV3)*(notV4)*V5) = 1 (notG)*F*(notV3)*(notV4)*V5 = 1 F = 1, V5 = 1 Сосуд финикийский и изготовлен в Vв.

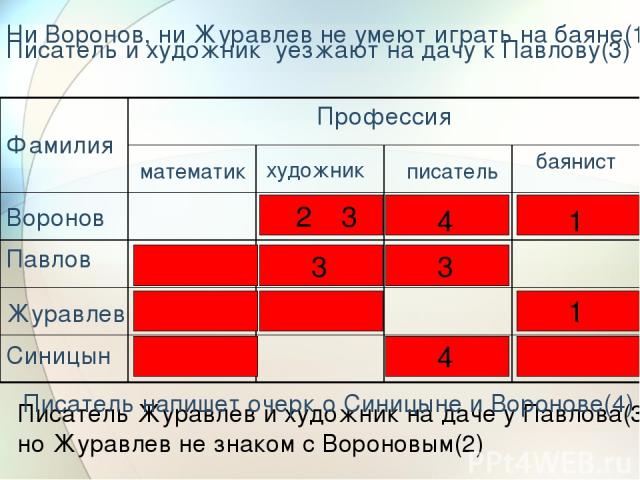
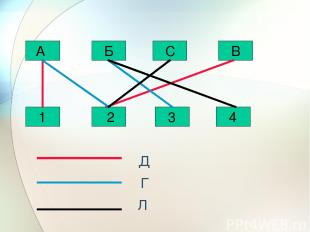
Задача 3 В одном доме живут Воронов, Павлов, Журавлев, Синицын. Один из них -математик, другой – художник, третий – писатель, а четвертый – баянист. ни Воронов, ни Журавлев не умеют играть на баяне; Журавлев не знаком с Вороновым; писатель и художник в воскресенье уезжают на дачу к Павлову; писатель собирается написать очерк о Синицыне и Воронове. Кто есть кто?

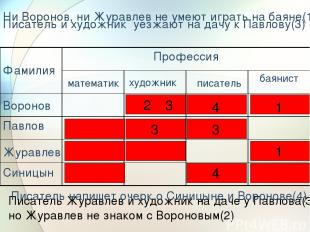
1 1 3 3 4 4 2 3 Писатель Журавлев и художник на даче у Павлова(3) но Журавлев не знаком с Вороновым(2) Журавлев Синицын Воронов Ни Воронов, ни Журавлев не умеют играть на баяне(1) Писатель и художник уезжают на дачу к Павлову(3) Писатель напишет очерк о Синицыне и Воронове(4) писатель математик художник Фамилия Профессия баянист Павлов

Воронов - математик, Павлов - баянист, Журавлев - писатель, Синицын - художник.

Физкультминутка Растирание рук, массаж всех пальцев: Надавливаем на суставы пальцев с боков, а также сверху – снизу. «Кулак – кольцо» : поочередно: одной рукой кулак, другой большой и указательный пальцы образуют кольцо. «Вертолет»: перемещаем карандаш между пальцами кисти. «Колечко»: поочередно и как можно быстрее перебираем пальцы рук, соединяя в кольцо с большим пальцем последовательно указательный, средний и т. д. в прямом и обратном порядке.

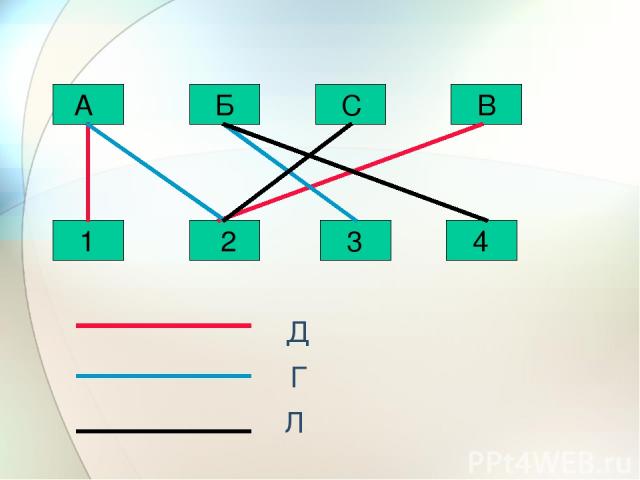
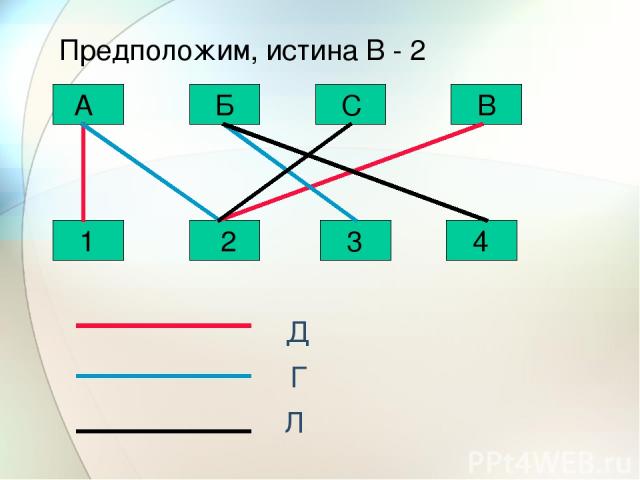
Задача 4 На соревнованиях по легкой атлетике Андрей, Боря, Сережа и Володя заняли первые четыре места. Мнения девочек разошлись, как места распределились между победителями. Даша. Андрей был первым, Володя – вторым Галя. Андрей был вторым, Борис – третьим Лена. Боря был четвертым, Сережа – вторым.

Ася, которая была судьей на этих соревнованиях, сказала, что каждая из девочек сделала одно правильное и одно неправильное заявление. Кто из мальчиков какое место занял?

С Б А В 1 2 3 4 Д Г Л

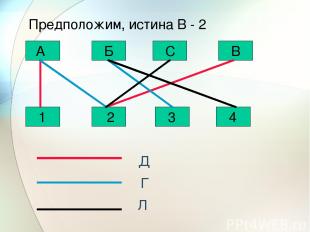
С Б А В 1 2 3 4 Д Г Л Предположим, истина В - 2

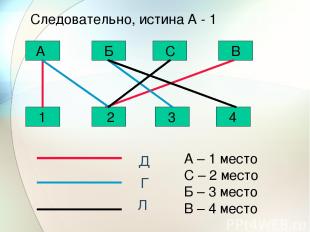
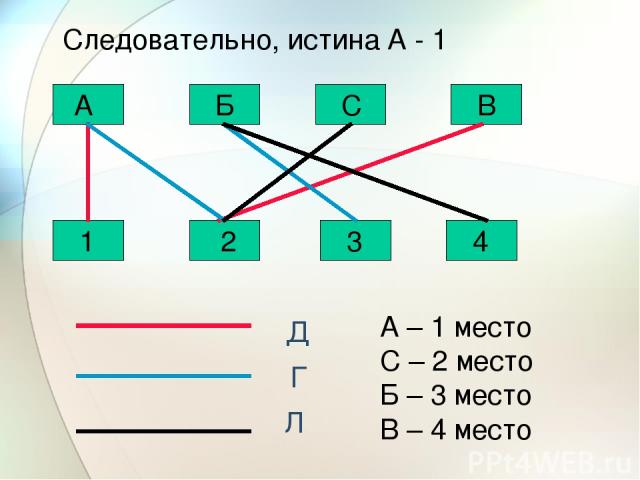
С Б А В 1 2 3 4 Д Г Л Следовательно, истина А - 1 А – 1 место С – 2 место Б – 3 место В – 4 место

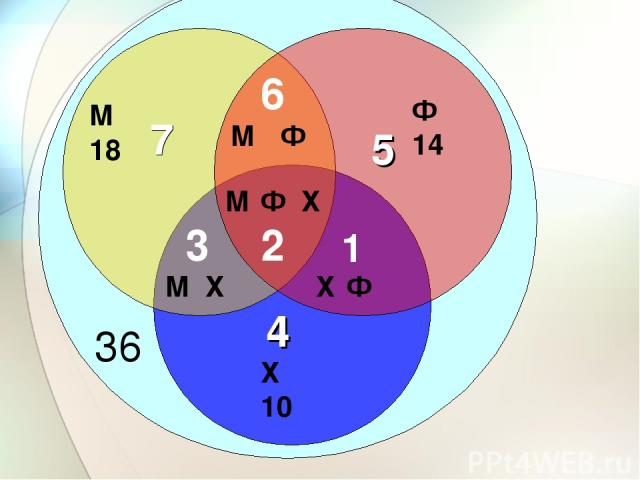
Задача 5 В классе 36 человек. Ученики посещают математический, физический и химический кружки. Математический посещают 18 человек, физический – 14, химический – 10. Кроме того, 2 человека посещают все 3 кружка, 8 – и математический и физический, 5 – и математический и химический, 3 - и физический и химический. Сколько учеников не посещают никаких кружков?

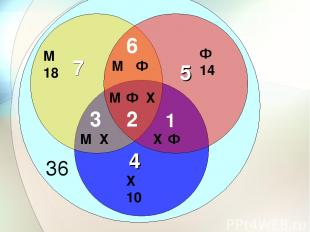
М 18 Ф 14 2 6 3 1 Х 10 7 4 5 36

36-(7+6+5+3+2+1+4)=8 8 учеников не посещают кружки.

Задачи для самостоятельного решения В очереди стоят Вика, Соня, Боря, Денис и Алла. Вика стоит впереди Сони, но после Аллы. Боря и Алла не стоят рядом; Денис не находится рядом ни с Аллой, ни с Викой, ни с Борей. Третьим в очереди стоит: 1.Боря 2.Соня 3.Вика 4.Алла 5.Денис

Три фигуры вырезали из бумаги, окрасили сверху и снизу в зеленый, красный и синий цвет, причем каждый цвет и сверху и снизу использовали по одному разу. Известно, что только у круга обе стороны одного цвета. Ромб ни с одной стороны не синий. Квадрат сверху красный, а снизу – зеленый красный синий не зеленый определенно сказать нельзя

На одном заводе работали три друга: слесарь, токарь и сварщик. Их фамилии Борисов, Иванов и Семенов. У слесаря нет ни братьев, ни сестер. Он – самый младший из друзей. Семенов, женатый на сестре Борисова, старше токаря. Назовите фамилии слесаря, токаря и сварщика.

В одной семье было много детей. Семеро из них любили капусту, шестеро – морковь, пятеро – горох. Четверо любили капусту и морковь, трое – капусту и горох. двое – морковь и горох. А охотно один ел и капусту, и морковь, и горох. Сколько в семье детей?  

В семье Семеновых пять человек: муж, жена, их сын, сестра мужа и отец жены. Все они работают. Один – инженер. Другой – юрист, третий – слесарь, четвертый – экономист, пятый – учитель. Вот что еще известно о них. Юрист и учитель не кровные родственники. Слесарь хороший спортсмен. Он пошел по стопам экономиста и играет в футбол за сборную завода. Инженер старше жены брата, но моложе, чем учитель. Экономист старше, чем слесарь. Назовите профессии каждого члена семьи Семеновых.

В авиационном подразделении служат Потапов, Щедрин, Семенов, Коновалов и Самойлов. Их специальности (они перечислены не в том же порядке, что и фамилии): пилот, штурман, бортмеханик, радист и синоптик. Об этих людях известно следующее: Щедрин и Коновалов не умеют управлять самолетом. Потапов и Коновалов готовятся стать штурманами. Щедрин и Самойлов живут в одном доме с радистом.

Семенов был в доме отдыха вместе со Щедриным и сыном синоптика. Потапов и Щедрин в свободное время любят играть в шахматы с бортмехаником. Коновалов, Семенов и синоптик увлекаются боксом. Радист боксом не увлекается. Какую специальность имеет Семенов?

На столе 3 совершенно одинаковых ящичка. В одном их них лежат 2 черных шарика, в другом – черный и белый, в третьем – 2 белых. На крышках ящичков есть надписи: «2 черных», «2 белых», «черный и белый». Однако известно, что ни одна из этих надписей не соответствует действительности. Сможете ли вы, вынув наугад шарик (и не заглядывая в ящички) определить, где какие шарики лежат?

Четверо друзей: Алексей Иванович, Федор Семенович, Валентин Петрович и Григорий Аркадьевич – были как-то раз со своими детьми в парке культуры и отдыха. Они катались на «колесе обозрения». В кабинах колеса оказались вместе: Леня с Алексеем Ивановичем, Андрей с отцом Коли, Тима с отцом Андрея, Федор Семенович с сыном Валентина Петровича, а Валентин Петрович с сыном Алексея Ивановича. Назовите кто чей сын и кто с кем катался, если ни один из мальчиков не катался со своим отцом.

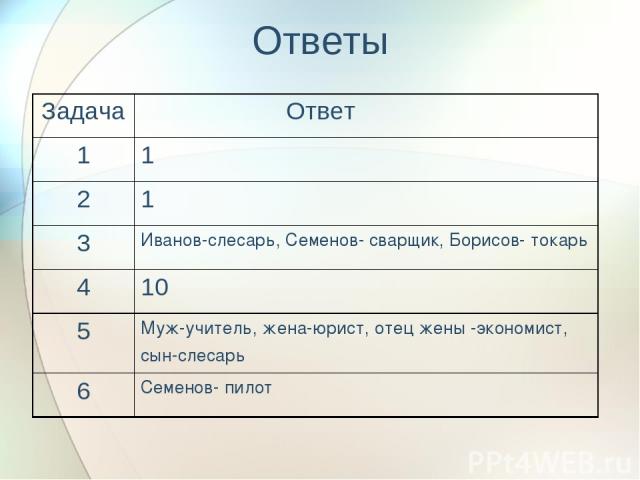
Ответы Задача Ответ 1 1 2 1 3 Иванов-слесарь, Семенов- сварщик, Борисов- токарь 4 10 5 Муж-учитель, жена-юрист, отец жены -экономист, сын-слесарь 6 Семенов- пилот

Задача Ответ 7 Нужно вынуть шарик из ящика «ч+б», 1) если шарик «б», то второй тоже «б». Ящик «2ч» будет содержать «ч+б», ящик «2б» будет содержать «2ч». 2) если шарик «ч», то второй тоже «ч». Ящик «2б» будет содержать «ч+б», ящик «2ч» будет содержать «2б». 8 Тима сын Алексея Ивановича, Андрей – сын Валентина Петровича, Леня – сын Григория Аркадьевича, Коля – свн Федора Семеновича. Катались: Леня с Алексеем Ивановичем, Андрей с Федором Семеновичем, Тима с Валентином Семеновичем, Коля с Григорием Аркадьевичем

Желаем удачи!