Презентация на тему: Задания по квадратным уравнениям

ФРАНЦУЗСКИЙ ПИСАТЕЛЬ ХIХ СТОЛЕТИЯ АНАТОЛЬ ФРАНС ОДНАЖДЫ ЗАМЕТИЛ: «УЧИТЬСЯ МОЖНО ВЕСЕЛО…ЧТОБЫ ПЕРЕВАРИВАТЬ ЗНАНИЯ, НАДО ПОГЛОЩАТЬ ИХ С АППЕТИТОМ» УЧИТЕЛЬ МАТЕМАТИКИ: МАЙСТРЕНКО В.М. БИБЛИОТЕКАРЬ: ХОЗИВАЛИЕВА М.П. АСТРАХАНЬ. МБОУ ЛИЦЕЙ №2 «ИМЕНИ В.В. РАЗУВАЕВА» ИБЦ 2012Г. КВАДРАТНЫЕ УРАВНЕНИЯ 900igr.net

Цели урока: Закрепить: знание формул квадратного уравнения; 2)формулы сокращенного умножения; Развивать культуру математической речи, уметь выступать перед аудиторией подготовленным сообщением. Приучать работе со справочной, дополнительной литературой.

ЭНЦИКЛОПЕДИИ ПО МАТЕМАТИКЕ ДЛЯ УЧАЩИХСЯ Тематическое расположение материала: история математики, числа, фигуры, детерминизм и случайность, фундамент математики, математика за работой . Алфавитное расположение материала.200статей, посвящённых основным понятиям математики, великим математикам всех времён. Биографии учёных даны в приложении к другим статьям.

В энциклопедии две части Первая (основная) и вторая (дополнительная). 10 разделов, где статьи, относящиеся к теме раздела расположены в алфавитном порядке.

Вспомогательные указатели Путеводители по тексту, представляющие собой упорядоченное по алфавиту или другому признаку множество рубрик, отражающих информацию о каких – либо объектах, описываемых или упоминаемых в тексте.

СПРАВОЧНЫЙ АППАРАТ КНИГИ Аннотация: это краткое изложение содержания книги. Предисловие: вводный текст, предваряющий изложение основного материала. Содержание: Система заголовков всех значительных частей книги с указанием страниц, где они помещены. Приложение: Помещается в конце издания, включает материалы, дополняющие основной текст издания.

Рубрика состоит из заголовка на страницу текста называющего тему, предмет, имя и ссылки. Типы вспомогательных указателей: Именной указатель; Предметный указатель; Хронологический указатель и другие… Архимёд (около 287—212 до н. э.) — древнегреческий математик, механик. Открыл закон, названный его именем. Обосновал закон рычага. Изобрёл «архимедов винт», полиспаст, червячную зубчатую передачу, прибор для измерения видимого диаметра Солнца, способ определения состава сплавов взвешиванием изделий в воде 39, 48, 49, 55

КРУГ часть плоскости, ограниченная окружностью (содержащая ее центр). Площадь круга S =∏ R2, где R — радиус окружности, а ∏ =3,141592654 — отношение длины окружности к диаметру

КВАДРАТ (от лат. quadratus — четырехугольный), 1) прямоугольник с равными сторонами. 2) Вторая степень числа ( а), то есть а × а = а²

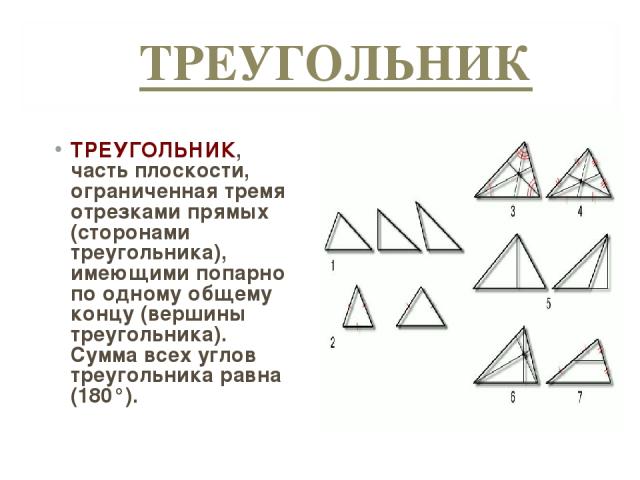
ТРЕУГОЛЬНИК ТРЕУГОЛЬНИК, часть плоскости, ограниченная тремя отрезками прямых (сторонами треугольника), имеющими попарно по одному общему концу (вершины треугольника). Сумма всех углов треугольника равна (180°).

Что объединяет эти картинки?

В корень смотреть – вникать в существо дела.

КОМАНДА «ТРЕУГОЛЬНИКИ» Решите квадратные уравнения и угадайте фамилию одного известного французского математика. И х2 - 3х - 4 =0 Т х2 + 4х + 3 =0 В х2 -2х =0 Е х2 – 4 =0 0;2 4;-1 2;-2 -1;-3

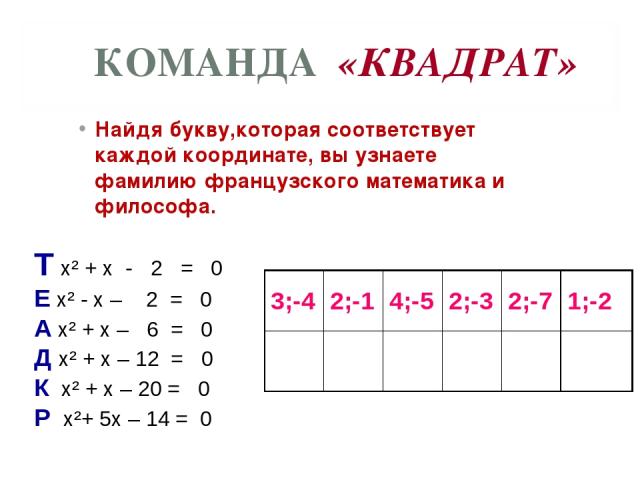
КОМАНДА «КВАДРАТ» Найдя букву,которая соответствует каждой координате, вы узнаете фамилию французского математика и философа. Т х² + х - 2 = 0 Е х² - х – 2 = 0 А х² + х – 6 = 0 Д х² + х – 12 = 0 К х² + х – 20 = 0 Р х²+ 5х – 14 = 0 3;-4 2;-1 4;-5 2;-3 2;-7 1;-2

КОМАНДА « КРУГ» Упростив выражения и расставив их по местам в таблице вы узнаете имя древнегреческого ученого (III в). А х² +4х – 12 = 0 Д х² + 8х - 9 = 0 И х² - 3х -4 = 0 Н х² - 9 = 0 О х² - 8х =0 T х² +10х + 25 =0 Ф х² - 8х - 9 = 0 -9;1 -1;4 0;8 -1;9 -6;2 -3;3 -5

РЕШЕНИЕ. (КОМАНДА «ТРЕУГОЛЬНИКИ») Франсуа Виет (1540- 1603) (0;2) (4;-1) (2;-2) (-1;-3) в и е т

РЕШЕНИЕ. (КОМАНДА «КВАДРАТ») Рене Декарт (1596 -1650) 3;-4 2;-1 4;-5 2;-3 2;-7 1;-2 Д Е К А Р Т

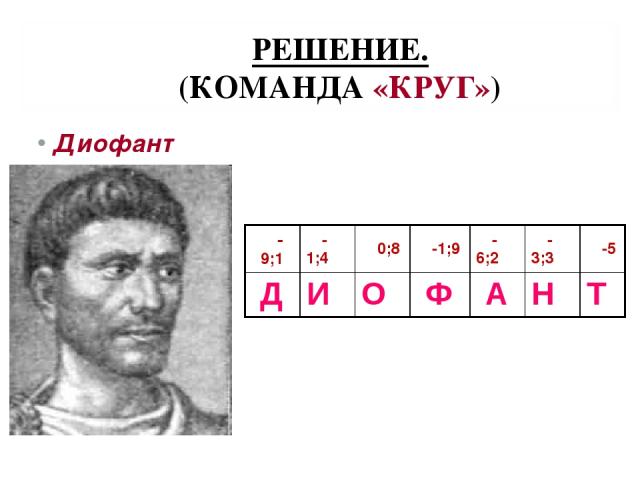
РЕШЕНИЕ. (КОМАНДА «КРУГ») Диофант -9;1 -1;4 0;8 -1;9 -6;2 -3;3 -5 Д И О Ф А Н Т

ИСТОРИЯ КВАДРАТНОГО УРАВНЕНИЯ. Квадратные уравнения в Индии. Задачи на квадратное уравнение встречаются в астрономическом трактате» Ариабхаттиам»составленном в 499г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый – Брахмагупта (VIIв) изложил общее правило решения квадратных уравнений. Его правило по существу совпадает с современным.

Формы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в «Книге абаха», написанной в 1202г. Итальянским математиком Леонардо Фибоначчи. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х²+ bx= c было сформировано в Европе в 1544г.М.Штифелем.Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские ученые Тарталья, Кардано, Бомбелли среди первых в ХVIв. Учитывают,помимо положительных, и отрицательные корни. Лишь в ХVIIв. Благодаря трудам Жиррара, Декарта, Ньютона и других ученых, способ решения квадратных уравнений принимает современный вид. Квадратные уравнения в в Еропе(ХIII―ХVIIвв)

Квадратные уравнения в Древнем Вавилоне. Квадратные уравнения умели решать вавилоняне около 2000лет до н.э. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

1. Уравнение x2+9=0 имеет два корня. 2.В уравнении x2-2x+1=0 единственный корень. 3. В уравнении x2-5x+3=0 сумма корней равна 5. 4. В уравнении x2+3x=0 один из корней есть иррациональное число. 5. В уравнении x2=0 дискриминант равен 0. 6. Уравнение x2-8x-3=0 не имеет корней. 7. Корнями уравнения x2-100x+99=0 являются числа 99 и 1. 8. Произведение корней уравнения x2-11x+9=0 равно 9. 10. Уравнение x2-9x+8=0 является неполным. 11. Если дискриминант уравнения – число отрицательное, то уравнение не имеет корней. 12. Уравнение x2-1056=0 корни являются противоположными числами. Спасибо Д С П М А К С И Р Б О

ОБЗОР КНИГ ПО МАТЕМАТИКЕ 1. Гусев В.А., Мордкович А.Г. Математика :Справ. материалы:Кн.для уч–ся–М.: Просвещение,1990 -416с.:ил. 2.Математика:Справочник школьника -М.:Слово, 1995-574с. 3. Пичурин Л.Ф. За страницами учебника алгебры: Кн. Для уч-ся 7-9 кл. – М.: Просвещение,1990 -224с.: ил. 4.Тучнин Н.П.Как задать вопрос?(О мат. творчестве школьников)- М.: Просвещение-1993 -192с.:ил.

Список литературы, использованной для практической работы. 1. Большая советская энциклопедия /Гл. ред. Прохоров А.М.- 3-е изд. – М.: Советская энциклопедия,1970 - 30 томов. 2.Математический энциклопедический словарь/ Глав. ред. Прохоров Ю.В.- М.: Большая Российская энциклопедия, 1995-846с. 3. Математика: Школьная энциклопедия /Гл. ред. Никольский С.М. – М.: Большая Российская энциклопедия,1996, -527с. 4.Энциклопедический словарь юного математика /Сост. Савин А.П. – М.: Педагогика,1985.-352с. 5.Энциклопедия для детей. Т.11 Математика. / Глав. ред. Аксенова М.Д.- М.: Аванта +, 1998.- 688с. 6. Самин Д.К. Сто великих открытий - М.: Вече, 2002-480с. 7. Самин Д.К. Сто великих ученых - М.: Вече, 2003-592с.