Презентация на тему: Статистическое определение вероятности

Статистическое определение вероятности. Решение задач.

Диктант. Запишите формулу вычисления вероятности случайного события в классической модели. Поясните, что означает каждая буква в этой формуле.Запишите формулу вычисления вероятности случайного события в статистической модели. Поясните, что означает каждая буква в этой формуле.Какому условию должны удовлетворять исходы опыта, чтобы можно было воспользоваться классическим определением вероятности? Чему равна частота достоверного события? Чему равна частота невозможного события?

Решение задач. Задача 1. В партии из 100 деталей отдел технического контроля обнаружил 5 нестандартных деталей. Чему равна относительная частота появления нестандартных деталей? Решение. w = 5/100 = 0,05 Ответ: w = 0,05.

Решение задач. Задача 2. При стрельбе из винтовки относительная частота попадания в цель оказалась равной 0,85. Найти число попаданий, если всего было произведено 120 выстрелов. Решение. Ответ: 102 попадания.

Вероятностная шкала. Что вероятнее?

Попытаемся расположить на специальной вероятностной шкале события: А={в следующем году первый снег в Москве выпадет в воскресенье};В={свалившийся со стола бутерброд упадет на пол маслом вниз};С={при бросании кубика выпадет шестерка};D={пpu бросании кубика выпадет четное число очков};Е={в следующем году снег в Москве вообще не выпадет};F={пpu бросании кубика выпадет семерка};G={в следующем году в Москве выпадет снег};Н={при бросании кубика выпадет число очков, меньшее 7}.

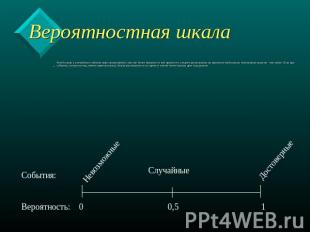
Вероятностная шкала Чем больше у случайного события шансов произойти, тем оно более вероятно и тем правее его следует расположить на вероятностной шкале; чем меньше шансов - тем левее. Если два события, на наш взгляд, имеют равные шансы, будем располагать их в одном и том же месте шкалы друг над другом.

Пример 1. Вова хочет вытянуть наугад одну карту из колоды с 36-ю картами. Маша, Саша, Гриша и Наташа предсказали следующее: Маша: Это будет король.Саша: Это будет пиковая дама.Гриша: Эта карта будет красной масти.Наташа: Эта карта будет пиковой масти.

Решение : Как сравнить между собой шансы предсказателей?Обозначим все события, предсказанные ребятами, буквами:А={Вова достанет короля};В={Вова достанет пиковую даму};С={Вова достанет карту красной масти};D={Вова достанет карту пиковой масти}.Всего в колоде: королей - 4; Р(А)=4/36пиковая дама - 1; Р(В)=1/36карт красных мастей-18; Р(С)=18/36пик- 9; Р(D)=9|36

Пример 2. Что вероятнее: А={получить шестерку при подбрасывании кубика} или В={вытянуть шестерку из перетасованной колоды карт}? Как и в предыдущем примере, подсчитаем шансы за осуществление каждого из этих событий. На кубике одна шестерка; в колоде четыре шестерки. Стало быть, событие. В более вероятно? Нет, конечно! Просто мы неверно считали шансы. Ведь когда речь идет о шансах, то говорят не просто «два шанса» или «один шанс», а «два шанса из трех» или «один шанс из тысячи».В примере 1 это не могло привести к ошибке, поскольку там все шансы были «из 36». А вот в этом примере ситуация сложнее:шестерок на кубике -1, а всего граней у куба - 6; шестерок в колоде - 4, а всего карт в колоде - 36.

Решение : Ясно, что «1 шанс из 6» лучше, чем «4шанса из 36», ведь 1/6 больше 4/36.Таким образом, шансы имеет смысл сравнивать как дроби: в числителе - сколько шансов за осуществление данного события, а в знаменателе - сколько всего возможно исходов. Понятно, что если знаменатели одинаковые, то можно сравнивать только числители (что и было сделано в примере 1).

Пример 3. Попробуем на основе нашего опыта общения по телефону сравнить между собой степень вероятности следующих событий: А ={вам никто не позвонит с 5 до 6 утра};В ={вам кто-нибудь позвонит с 5 до 6 утра};С ={вам кто-нибудь позвонит с 18 до 21};D ={вам никто не позвонит с 18 до 21}.

Решение : Ранним утром звонки бывают очень редко, поэтому событие А - очень вероятное, почти достоверное, а В - маловероятное, почти невозможное.Вечерние часы, наоборот, время самого активного телефонного общения, поэтому событие С для большинства людей вероятные, чем D. Хотя, если вам вообще звонят редко, D может оказаться вероятнее С.

Решение задач. Задача 3. При проведении контроля качества среди 1000 случайно отобранных деталей оказалось 5 бракованных. Сколько бракованных деталей следует ожидать среди 25 000 деталей? По результатам контроля можно оценить вероятность события А={произведенная деталь бракованная}. Приближенно она будет равна его частоте: Р(А) = 5/1000=0,005.Следует ожидать такую частоту и в будущем, поэтому среди 25 000 деталей окажется около 25 000 • 0,005 = 125 бракованных.

Решение задач. Задача 4. Население города Калуги составляет около 400 000 жителей. Сколько калужан родились 29 февраля?Заметим прежде всего, что вопрос задачи не совсем корректен: мы можем ответить на него лишь приближенно, ибо реальная частота даже в такой большой выборке из 400 000 жителей не обязана совпадать с вероятностью.29 февраля бывает только в високосном году — один раз в четыре года, следовательно, для случайно выбранного человека его день рождения попадает на 29 февраля с вероятностьюЭто значит, что среди 400 000 жителей Калуги следует ожидать около человека, которым приходится праздновать свой день рождения раз в четыре года.

Решение задач. Задача 5. Из озера выловили 86 рыб, которых пометили и отпустили обратно в озеро. Через неделю произвели повторный отлов, на этот раз поймали 78 рыб, среди которых оказалось 6 помеченных. Сколько приблизительно рыб живет в озерОказывается, найти ответ на этот неожиданный вопрос совсем несложно.В самом деле: обозначим неизвестную нам численность рыб в озере через N.Тогда вероятность поймать помеченную рыбу в озере будет 86/N.С другой стороны, эта вероятность должна приближенно равняться полученной во втором улове частоте: 86/N=6/78.Отсюда N = 86 • 78 / 6 = 1118. е?

Домашнее задание: В письменном тексте одной из «букв» считается пробел между словами. Найдите частоту просвета в любом газетном тексте.