Презентация на тему: Квадратный корень из числа

Определите какое действие выполняется? 82 = , 52 = , ( ½ )2 = Впишите в квадрат соответствующие числа Определите какое действие выполняется? Впишите в квадрат соответствующие числа Действие нахождения числа по его квадрату называется извлечением квадратного корня Знаком квадратного корня является По квадрату находим ___________________ По числу находим ___________________ Квадратным корнем из числа а называется число, квадрат которого равен а. 900igr.net

± 8 ± 5 ± ½ ,следовательно, Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.

Подкоренное выражение должно быть _____________________ Извлечение квадратного корня из отрицательного числа _________________________________________________________ Так как корень арифметический, то его значение должно быть _______, следовательно, значение корня должно быть __________________ . При извлечении квадратного корня из четной степени не забывать ________________ ≥ 0 ≥ 0 ≥ 0

Чтобы извлечь корень из четной степени, надо показатель подкоренного выражения ________________________________ Чтобы извлечь корень из четной степени надо показатель подкоренного выражения __________________________________ 32 х6 разделить на 2 разделить на 2

Подкоренное выражение – точный квадрат Подкоренное выражение – неточный квадрат Бесконечная непериодическая десятичная дробь – называется иррациональным числом π = 3,1415… Точно вычисляются корни, подкоренные выражения которых являются ______________________________ точный квадрат

Чтобы вычислить такой корень, надо найти такое число, которое при возведении в квадрат дает __________________________________ Чтобы освоить вычисление корня, надо знать: 1. Знать таблицу степеней; Заполните таблицу

Чтобы освоить вычисление корня, надо знать и уметь: 1. Знать таблицу степеней; 2. Уметь раскладывать числа на простые множители; 3. Знать, что число, оканчивающее нулями, будет точным квадратом, если число нулей четно; 4. Знать, что десятичная дробь в квадрате имеет после запятой четное число знаков ; Чтобы извлечь корень надо: извлечь корень из числа без нулей и приписать нулей в два раза меньше 2 0 • • , Чтобы извлечь корень из дроби надо: извлечь корень из числа без запятой справа отсчитать в два раза меньше знаков, чем подкоренном выражении • 0 , 0 0

Чтобы освоить вычисление корня, надо знать и уметь: Вычислите: Определите какое число в квадрате дает подкоренное выражение: (122 = 144). Это число и будет ответом. 302 = 900, 402 = 1600 900 < 1225< 1600 Так как 1225 оканчивается на 5, то искомое число должно оканчиваться на 5. Это 35. Проверим 35 · 35 =1225 Ответ: 35 35 1. Корень из произведения; 2. Произведение корней; 2. Корень из дроби; 3. Деление корней; 1. Корень из четной степени; 2. Возведение корня в степень;

1. Корень из произведения; 2. Произведение корней; Приведите примеры: _____________________ _____________________ Чтобы извлечь корень из произведения, надо извлечь корни из _____________ ____________________________________ Чтобы перемножить корни, надо ____________________________________ ____________________________________ перемножить подкоренные выражения и извлечь корень из каждого множителя Вычислите:

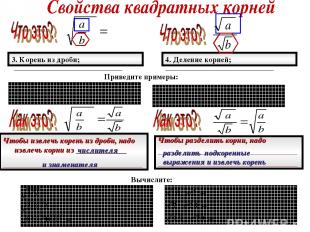
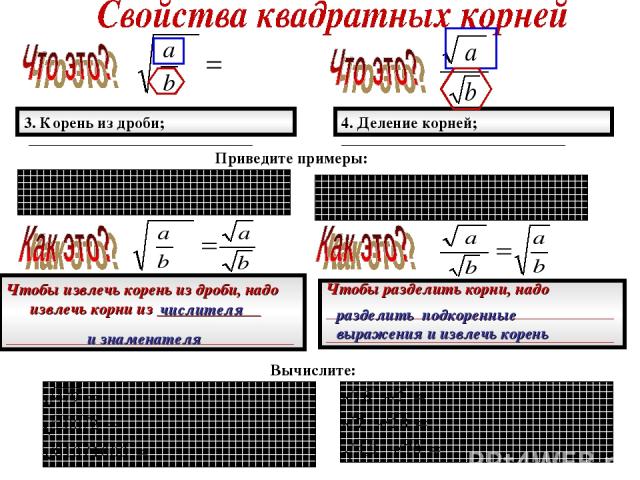
3. Корень из дроби; 4. Деление корней; Приведите примеры: _____________________ _____________________ Чтобы извлечь корень из дроби, надо извлечь корни из _____________ ____________________________________ Чтобы разделить корни, надо ____________________________________ ____________________________________ разделить подкоренные выражения и извлечь корень числителя и знаменателя Вычислите:

Вычислить: Разложим 1764 на множители

5. Возведение корня в квадрат; 4. Извлечение корня из четной степени; Возведение корня в квадрат, дает _________________________________ _________________________________ Чтобы извлечь корень из четной степени, надо ____________________________________ ____________________________________ разделить степень подкоренного выражения на 2 и ответ взять по модулю подкоренное выражение по модулю

Корень квадратный из а в квадрате равен а по модулю: Корень квадратный в квадрате равен подкоренному выражению Чтобы извлечь корень из четной степени, надо степень подкоренного выражения разделить на 2 и ответ взять по модулю: Корень квадратный, умноженный сам на себя равен подкоренному выражению