Презентация на тему: Формы работы на уроках математики в коррекционных классах

Формы работы на уроках математики в коррекционных классах Учитель математики ГБОУ СОШ № 201 Бадаева Екатерина Викторовна

Математика – один из предметов, который вызывает значительные затруднения у большинства учащихся. В обучении детей с интеллектуальными нарушениями нельзя ожидать, что навыки, умения, представления об окружающем удастся сформировать у детей в полном объеме. В зависимости от индивидуальных особенностей, ребенок может достигать определенного уровня успешности в том или ином виде деятельности.

Коррекционные классы созданы для обучения и воспитания детей, у которых при потенциально сохранных возможностях интеллектуального развития наблюдается: слабость памяти, внимания; недостаточность темпа и подвижности психических процессов; снижена работоспособность; недостаточна познавательная деятельность; плохо развита эмоционально-личностная сфера.

Коррекционная работа с детьми должна вестись по следующим направлениям: Осуществление индивидуального подхода к детям Предотвращение наступления утомления Использование методов, с помощью которых можно максимально активизировать познавательную деятельность детей Проявление особого педагогического такта. Важно подмечать и поощрять успехи детей, помогать каждому ребенку, развивать в нем веру в собственные силы и возможности Обеспечивать обогащение детей предметными знаниями (использование развивающих игр, упражнений с конкретными примерами и т. д.) при изучении математики

Выделяют 13 этапов урока в коррекционных классах: Организационный этап(начало урока) Этап проверки домашнего задания Этап устного счета Этап актуализации субъективного опыта учащихся Этап изучения нового материала Этап закрепления, тренировки и отработки умений Этап физкультминутки Этап применения знаний Этап обобщения и систематизации знаний Этап контроля и самоконтроля Этап информации о домашнем задании Этап подведения итогов занятия Этап рефлексии(конец урока) Комбинируя эти этапы в соответствии с логикой занятия и используя различные педагогические техники, можно получить разнообразные варианты уроков математики в коррекционных классах.

Организационный этап (начало урока) Задачи этапа - обеспечить комфортную внешнюю обстановку для работы, обеспечить положительный эмоциональный настрой. «Вход в урок» может быть разнообразным в зависимости от возраста и подготовки учащихся. Когда класс слабый, трудно настраивается, то начинать урок лучше всегда определенным образом, а если класс слажен, то начало урока можно разно- образить. Этап проверки домашнего задания Задачи этапа- установить правильность, полноту и осознанность выполнения домашнего задания всеми детьми; выявить пробелы в знаниях и способах деятельности учащихся; определить причины возникновения затруднений; устранить(по возможности) обнаруженные пробелы; обеспечить рефлексию учащихся по поводу своих способов решений и своих затруднений. Возможно предложить учащимся выбрать из нескольких вариантов ответов правильный(в зависимости от изучаемой темы); показательный ответ; устный опрос и т.д. Важно использовать наглядность и образцы решения! ( как и на любом другом этапе урока)

Например, домашним заданием было решить уравнения или найти нули функции 3х²-48=0 х²+4=-5х 4х²+1=0 у=3х²+х Карточки с условиями и возможные варианты решения ( правильное и с типичными ошибками) прикреплены к магнитной доске и учащиеся должны найти правильное решение заданий, сверив с решениями в тетрадях. На этом этапе важно обсудить не только правильное решение, но и указать , что неверно в других решениях. Так как домашнее задание в классах коррекции не может быть очень объемным, то такой способ проверки домашнего задания очень удобен и не занимает много времени. Так же обязательно нужно дать время детям на исправление ошибок в тетрадях.

Этап устного счета Задачи этапа – совершенствование навыков устных вычислений; закрепление математических понятий. Если хорошо проведен устный счет, то учащиеся активны и готовы к восприятию нового материала. Чаще всего устный счет проводится в такой форме: Найти сумму чисел 5 и (-3) Увеличить число 8 в 2 раза К какому числу надо прибавить (-20), чтобы получилось число (-25) Чему равна разность чисел (-3) и 7 и т.д. Безусловно, отрабатываются вычислительные навыки, но активность учащихся скорее будет снижаться, если использовать только такие виды работы. Учащиеся коррекционных классов плохо и с большим трудом усваивают задания на слух, следует учитывать это, а также не перегружать задания уровнем сложности. Необходимо уделить особое внимание приемам, активизирующим деятельность учащихся, обязательно проговаривая каждое правильное решение. Например: 1) даны числа (-3) и 0,2. Какие действия можно выполнить с этими числами? Выполнить возможные действия. 2) между числами расставить знаки математических действий так, чтобы равенства были верными: 3 4 = -1 0,5 (-1)= -0,5 ¾ ¼ = ½ 10 (-18)= 28 Прочитать примеры, в которых находили сумму, разность и т.п. 3) произведение корней какого из уравнений равно -4? х+4=0 2х²+х-4=0 х²-3х-4=0 х²-4=0 4) соотнести условие примера с одним из предложенных ответов: а²∙а а а а¹²:а а а ¹º

Этап устного счета 5) Возможно использовать графический диктант. Если пример решен верно, то ставим _ ,если нет, то ^ 1)0,6 ∙0,3=0,3 4)1,5∙100=1500 2)12:0,2=60 5) 5х²+х²=5х 3)-3-(-5)=2 6)число 5 составляет 20% от 20 Ключ к ответам: _^^_ _ _ ( или ставить + или -) 6) Устный счет возможно выполнить и с помощью цепочки действий, а правильный ответ выбрать из предложенных: -24,8-5х -5х-19 -5х-23 -5-5х 7) Задачи устного счета могут носить увлекательный характер. Например, «Винни-Пух и Пятачок собрали 30 шишек, что составило треть всех шишек под елкой.Сколько всего шишек было под елкой?» Можно использовать математические диктанты, перфокарту и т.д. Главное – постоянное обсуждение происходящих действий, включение детей в диалог.

Этап актуализации субъективного опыта учащихся Задачи этапа- обеспечить мотивацию учения школьников; обеспе- чить включение детей в совместную деятельность по определению целей урока Возможно объяснить учащимся цели урока одновременно с сообщением темы занятия; сообщить цели в виде проблемного задания. Например, если правильно найдете корни уравнений и заполните таблицу ответов, то сможете прочитать тему урока 35–х=17 У 29+х=45 О у–37=18 Е 90–у=62 И 31+у=16+44 Ж 80–х=19+21 Н 40–3=с+13 М Это же задание возможно дать на устном счете, где надо будет расположить корни уравнений по возрастанию и составить слово (изменив соответствие букв в заданиях)

Этап актуализации субъективного опыта учащихся Возможно выяснить тему урока следующим образом: 3+18=? 120:4=? ?·9=630 500-30=? Написать названия неизвестных компонентов. (сумма, частное, множитель, разность) Одно из этих слов лишнее в логической цепочке. Подумайте, что это за слово и каким его нужно заменить. Почему? (множитель – произведение) Произведение – это результат какого действия? Сегодня на уроке и будем говорить об УМНОЖЕНИИ.

Этап изучения нового материала Задачи этапа- обеспечить восприятие, осмысление и первичное запоминание нового материала. При изучении новых геометрических фигур очень хорошо исполь- зовать следующий вид работы: К доске выходит ребенок и встает спиной к ней. На доске учитель делает рисунок, например, параллелограмм, отметив, что противоположные стороны равны и параллельны Учащиеся должны, не называя эту фигуру, объяснить стоящему у доски отличительные свойства фигуры так, чтобы ученик смог назвать эту фигуру. После этого второй ученик пытается отгадать, что же за фигура теперь на доске, если дети пытаются описать отличи- тельные свойства ромба по рисунку, а такую фигуру еще не изучали.

Этап закрепления, тренировки и отработки умений Задачи этапа- обеспечить закрепление учащимися знаний и способов действий, которые им необходимы для самостоятельной работы; создать условия для выявления школьниками индивидуальных способов закрепления изучаемого материала. На этом этапе важно следить за оформлением решений и точно следовать алгоритму выполнения заданий (наглядность!) Ученики должны комментировать каждое действие, используя правила. Позже дети пробуют самостоятельно выполнить аналогичные задания. Например, отработку формул сокращенного умножения можно выполнить следующим образом: (a-b)²= a²-2ab+b² a²-b²=(a-b)(a+b) (a+b)²=a²+2ab+b² Расположить следующие выражения в столбик с соответствующей формулой и применить ее: (у-3)² а²+2а+1 х²-4 9+6с+с² 36-х² (5+b)² и т.д. При закреплении хорошо использовать вычислительную цепочку, задание с формулировкой «Найди ошибку!»

Этап физкультминутки или отдыха Задачи этапа- обеспечить отдых учащихся в зависимости от вида утомления; настроить детей на дальнейшую работу. Физкультминутка не должна надоедать, не слишком возбуждать детей. Если на уроке происходит частая смена видов деятельности и материал не перегружен уровнем сложности, то физкультминутку можно не проводить. На этом этапе можно провести устную разминку. Петух, стоя на одной ноге, весит 3 кг. Сколько он весит, стоя на двух ногах? Сколько концов у 3,5 палок? Над рекой летели голубь, щука, две синицы, стриж и пять углей. Сколько птиц летело? В одной семье 2 отца и два сына. Сколько человек в семье?

Этап применения знаний Задачи этапа - обеспечить усвоение учащимися знаний и способов деятельности на уровне их применения в разнообразных ситуациях; развивать у детей умение самостоятельно применять знания в раз- личных ситуациях с учетом своего личного опыта. Например, предлагается упростить выражения и соединить те, ответы которых одинаковы: 2а+3-а+7 4(а-1)-4а 7а-4-7а 15+а-5 5а-(3+2а) 5а-3(2-а) 10а-2(3-а) (6а-2)–(3а+1) Все ли выражения можно разбить по парам? Почему? Как нужно изменить условие последнего примера левого столбика, чтобы соединение стало возможным? 10а-2(3+а) или 6а-2(3-а)

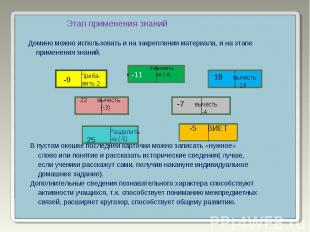
Этап применения знаний Домино можно использовать и на закреплении материала, и на этапе применения знаний. В пустом окошке последней карточки можно записать «нужное» слово или понятие и рассказать исторические сведения( лучше, если ученики расскажут сами, получив накануне индивидуальное домашнее задание). Дополнительные сведения познавательного характера способствуют активности учащихся, т.к. способствует пониманию межпредметных связей, расширяет кругозор, способствует общему развитию.

Этап обобщения и систематизации знаний Задачи этапа- обеспечить формирование у учащихся не только вычислительных навыков, но и понимания полученных знаний, обеспечить понимание внутрипредметных и межпредметных связей. Например, геометрическая задача следующего содержания: «Чему может быть равен периметр равнобедренного треуголь- ника, если две его стороны равны 4см и 3см» решается с помощью уравнения. Необходимо тщательно прописать этап составления и решения уравнения. Также задача поискового характера, важно, чтобы дети увидели сами два способа решения. Следующие задания предполагают понимание понятий и определений: 1) из предложенных терминов выбрать два, которые наиболее точно определяют понятие УРАВНЕНИЕ СУММА РАВЕНСТВО ПРОИЗВЕДЕНИЕ НЕИЗВЕСТНОЕ КОРЕНЬ 2) заполнить пропуски в предложениях: «Уравнение вида _ х +b_ +_ =0 называется квадратным, где а __, х -___________ , a,b,c - _______». « ______________ уравнение называется приведенным, если ____». « Квадратное уравнение станет линейным, если _______».

Этап информации о домашнем задании Задачи этапа- обеспечить понимание учащимися содержания и способов выполнения домашнего задания. Если уж задавать - то с максимальной пользой! Домашнее задание может быть разноуровневым индивидуальным домашнее задание с инструкцией творческое Любое домашнее задание нужно обсудить. Если возникли вопросы, то найти в «копилке»( ведем в конце тетради) образцы выполнения аналогичных заданий. Этап подведения итогов Задачи этапа- оценить работу всего класса и отдельных учащихся Обязательно отметить и похвалить тех детей, которые проявили активность на уроке, даже если что-то не получи- лось.

Этап рефлексии( конец урока) Задачи этапа- способствовать осознанию детьми своего эмоциональ- ного состояния, своей деятельности, взаимодействия с учителем и одноклассниками. Возможно предложить учащимся в конце урока выразить свои впечатления об общей работе и своей личной, ответив на вопросы: 1. Как я оцениваю свою работу на уроке? Работал в полную силу, своей работой удовлетворен Работал вполсилы Не работал 2. Нравится ли такой вид работы? Да Не очень Нет Можно предложить детям составить предложение, в котором все слова начинаются с одной буквы. Вот ветер все воет, вьюжит. Предложение можно составить по теме урока: Дружно делим дроби. Возможно и такое задание: составить как можно больше слов из слова ТРАНСПОРТИР ( на время) Такая работа обязательно вызовет положительные эмоции!